假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 在其他有关条件保持不变的情况下，下列叙述正确的是A.置信区间值越大，置信区间范围越宽 B.罝信区间值变小，罝信区间范围不变 C.显著性水平值越大，罝信区间范围越宽 D.显著性水平值越小，S信区间范围越窄
题目
B.罝信区间值变小，罝信区间范围不变
C.显著性水平值越大，罝信区间范围越宽
D.显著性水平值越小，S信区间范围越窄
相似考题
更多“假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 在其他有关条件保持不变的情况下，下列叙述正确的是”相关问题
-
第1题：
当从一万个高考生的成绩中（正态分布）随机抽取容量为1 000的样本时，其样本方差与总：体方差的比值分布是()分布。A.T分布
B.Z分布
C.F分布
D.X2分布答案：D解析：推断统计；假设检验。 当从正态分布的总体中随机抽取容量为n的样本时，其方差与总体方差的比值分布是卡方分布。 -
第2题：
已知某次高考的数学成绩服从正态分布，从这个总体中随即抽取n=37的样本，并计算得其平均分为79分，标准差为9分。那么下列成绩不在这次考试中全体考生成绩均值μ的0．95置信区间之内的是（ ）A.77
B.80
C.81
D.85答案：D解析：本题旨在考查考生对区间估计知识点的掌握程度。根据题意可知，本题属于“总体方差未知时，用样本的无偏方差
作为总体方差的估计值，实现对总体平均数μ的估计”的情况。且总体分布为正态分布，因此总体均值的置信区间为{img src="/main/97/u/2011040805490657152}frac{S}{sqrt{n-1}}" align='absmiddle'/} ，同时95％的概率推测即z=1．96。将题目中的已知量代入公式即
，也即73.1＜μ＜84.9。故本题的正确答案是D。
-
第3题：
假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 根据本次测验成绩，该测验分数的平均数的标准误
答案：A解析：题考察的是标准误的计算公式，总体正态，方差未知，则标准为
-
第4题：
某大学一家快餐店记录了过去5年每天的营业额，每天营业额的均值为2500元，标准差为400元，由于在某些节日的营业额偏高，所以每日营业额的分布是右偏的。从5年中随机抽取100天，计算其平均营业额，则其抽样分布是（）
- A、正态分布，均值为250元，标准差为40元
- B、正态分布，均值为2500元，标准差为40元
- C、右偏，均值为2500元，标准差为400元
- D、正态分布，均值为2500元，标准差为400元
正确答案:B -
第5题：
某学校统计学考试成绩服从正态分布，以往经验表明成绩的标准差为10分。从学生中随机抽取25个简单随机样本，他们的平均分数是84.32分。根据这些数据计算该校学生的统计学考试的平均成绩的95%的置信区间是（）
- A、84.32±39.2
- B、84.32±1.96
- C、84.32±3.92
- D、84.32±19.6
正确答案:C -
第6题：
假设某学校学生的年龄分布是右偏的，均值为23岁，标准差为3岁，如果随机抽取100名学生，下列关于样本均值抽样分布描述不正确的是（）。
- A、抽样分布的标准差等于0.3
- B、抽样分布近似服从正态分布
- C、抽样分布的均值近似为23
- D、抽样分布为非正态分布
正确答案:D -
第7题：
假设某班期末统计学考试成绩服从正态分布，平均成绩为70分，标准差为12分，要求计算： （1）随机抽取1人，该同学成绩在82分以上的概率； （2）随机抽取9人，其平均成绩在82分以上的概率。
正确答案:（1）15.86%, (2)0.135% -
第8题：
有关正态分布表述正确的是（）
- A、正态分布的概率可以采用函数Fdist（）计算
- B、正态分布的密度曲线图与二项分布相似
- C、标准正态分布的平均数为0，标准差为1
- D、正态分布的变量是一种离散型随机变量
正确答案:C -
第9题：
某灯泡公司生产的灯泡寿命服从均值为2000小时、标准差为30的威布尔分布，随机抽取100个样品组成一个样本做灯泡寿命试验，那样本寿命均值的分布应服从：（）
- A、均值为2000，标准差为3的威布尔分布
- B、均值为2000，标准差为30的威布尔分布
- C、均值为2000，标准差为3的正态分布
- D、均值为2000，标准差为30的正态分布
正确答案:C -
第10题：
多选题关于区间估计原理正确的是（）。A在其他条件相同的情况下，置信概率越大置信区间也越大
B在其他条件相同的情况下，置信概率越大置信区间越小
C根据正态分布的性质随机变量落在平均数两侧1个标准差范围内的概率为68.3%
D根据正态分布的性质随机变量落在平均数两侧1个标准差范围内的概率为95.45%
E当置信概率为95%时，意味着估计的可靠性为95%
正确答案： E,A解析： 暂无解析 -
第11题：
多选题已知某次物理考试非正态分布，σ=8，从这个总体中随机抽取n=64的样本，并计算得其平均分为71，那么下列成绩在这次考试中全体考生成绩均值μ的0.95的置信区间之内的有（）A69
B70
C71
D72
正确答案： B,D解析： 暂无解析 -
第12题：
单选题某学校统计学考试成绩服从正态分布，以往经验表明成绩的标准差为10分。从学生中随机抽取25个简单随机样本，他们的平均分数是84.32分。根据这些数据计算该校学生的统计学考试的平均成绩的95%的置信区间是（）A84.32±39.2
B84.32±1.96
C84.32±3.92
D84.32±19.6
正确答案： A解析： 暂无解析 -
第13题：
从100个住户中随机抽取了10户，调查其月消费支出额。经计算得到10户的平均月消费支出额为3500元，标准差为300元。假定总体服从正态分布，则总体平均月消费支
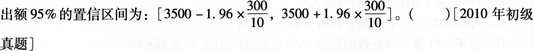答案：错解析：
-
第14题：
假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 该学区所有考生平均成绩的99%的罝信区间是A.73.20-74.80
B.72.04-75.96
C.72.36-75.64
D.71.42-76.58答案：D解析：计算置信区间，得到74±2.58xl,所以选71.42?6.58。 -
第15题：
某超市想要估平均金额，采取简单随机方式抽取49名顾客进行调查。假定从正态分布，且标准差为15元。如果样本均值为120元求总体均值95%的置信区间。
略 -
第16题：
从服从正态分布的无限总体中分别抽取容量为4，16，36的样本，当样本容量增大时，样本均值的标准差（）
- A、保持不变
- B、增加
- C、减小
- D、无法确定
正确答案:C -
第17题：
从服从正态分布的无限总体中分别抽取容量为13，32，45的样本，当样本容量增大时，样本均值的数学期望（），标准差（）
- A、保持不变；增加
- B、保持不变；减小
- C、增加；保持不变
- D、减小；保持不变
正确答案:B -
第18题：
从足够大的总体中随机抽取16份统计学的考试结果作为样本。样本中的平均分为78.6，方差为64.我们想知道总体的平均分是否大于75分。假设总体的成绩服从正态分布。据材料，检验统计量是（）
- A、0.45
- B、1.80
- C、3.6
- D、8
正确答案:B -
第19题：
从服从正态分布的无限总体中抽取容量为4，16，36的样本，当样本容量增大时，样本均值的标准差（）。
- A、保持不变
- B、无法确定
- C、增加
- D、减小
正确答案:D -
第20题：
某设备制造企业生产的小型设备服从平均寿命为40000小时的指数分布，抽取100个设备样本，计算出其平均寿命，则其平均寿命服从（）
- A、均值为40000小时的指数分布
- B、近似为均值是40000小时，标准差为40000小时的正态分布
- C、近似为均值是40000小时，标准差为4000小时的正态分布
- D、近似为均值是40000小时，标准差为400小时的正态分布
正确答案:C -
第21题：
设某地区高考成绩服从平均数为550，标准差为100的正态分布，随机抽取50人，以95.45%的概率保证程度估计该地区高考平均分数的区间在（）分
正确答案:521.72——578.28 -
第22题：
填空题设某地区高考成绩服从平均数为550，标准差为100的正态分布，随机抽取50人，以95.45%的概率保证程度估计该地区高考平均分数的区间在（）分正确答案： 521.72——578.28解析： 暂无解析 -
第23题：
单选题有关正态分布表述正确的是（）A正态分布的概率可以采用函数Fdist（）计算
B正态分布的密度曲线图与二项分布相似
C标准正态分布的平均数为0，标准差为1
D正态分布的变量是一种离散型随机变量
正确答案： A解析： 暂无解析
