假设总体X服从N（μ,σ2)。若2己知,样本容量和置信度均不变,那么用不同的样本观测值估计μ时,若μ变大,则置信区间的长度()A.变长 B.不变 C.变短 D.无法确定

题目
假设总体X服从N（μ,σ2)。若2己知,样本容量和置信度均不变,那么用不同的样本观测值估计μ时,若μ变大,则置信区间的长度()

A.变长
B.不变
C.变短
D.无法确定
相似考题

1.在估计某一总体均值时，随机抽取n个单元作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是( )。A．样本容量太小B．估计量缺乏有效性C．选择的估计量有偏D．抽取样本时破坏了随机性

2.从一个服从正态分布的总体中随机抽取样本容量为n的样本，在95%的置信度下对总体参数进行估计的结果为：20±0.08。如果其他条件不变，样本量扩大到原来的4倍，则总体参数的置信区间应该是（ ）。A.20±0.16B.20±0.04C.80±0.16D.80±0.04

3.以下关于置信区间与精度的关系说法不正确的是A、当置信度1-α增大，又样本容量n固定时，置信区间长度增加，区间估计精度减低B、置信区间的长度可视为区间估计的精度C、当置信度1-α减小，又样本容量n固定，置信区间长度减小，区间估计精度提高D、置信度1-α固定，当样本容量n增大时，置信区间长度增加，区间估计精度减低

4.假设总体X～N (μ,σ2),σ2已知，若样本容量和可靠程度均不变，则对于不同的样本观测值，总体均值μ的置信区间的长度( )。A．变长B．变短C．不变D．不能确定

更多“ 假设总体X服从N（μ,σ2)。若2己知,样本容量和置信度均不变,那么用不同的样本观测值估计μ时,若μ变大,则置信区间的长度()”相关问题

  • 第1题：

    假设当置信度1-α增大，样本容量n固定时，置信区间

    A、长度减少

    B、长度增大

    C、估计精度提高

    D、长度不变


    正确答案:B

  • 第2题：

    同一总体的两个样本中,以下哪种指标值小的其样本均数估计总体均数更可靠?( )

    A、Sx

    B、S

    C、x

    D、CV

    E、S2解析：标准误：一、用来衡量抽样误差大小，标准误越小，样本均数与总体均数越接近即样本均数的可信度越高；二、结合标准正态分布与t分布曲线下的面积规律，估计总体均数的置信区间；三、用于假设检验。


    参考答案：A

  • 第3题：

    设总体X～N(μ，σ2)，σ2已知，若样本容量和置信度均不变，则对于不同的样本观测值，总体均值μ的置信区间的长度( )。

    A．变长

    B．变短

    C．不变

    D．不能确定


    正确答案：C
    解析：对于σ2已知的总体正态分布，因为=1-α，所以总体均值μ的置信区间的长度为。在样本容量和置信度均不变的条件下，与样本观测值无关。所以对于不同的样本观测值，总体均值μ的置信区间的长度不变。

  • 第4题：

    设总体X~N(u,σ2)，u与σ2均未知，x1,x2,...,x9为其样本，样本方差，则u的置信度为0. 9的置信区间是：


    答案：C
    解析：

  • 第5题：

    若总体X～N(0,32),X1,X2,…,x9为来自总体样本容量为9的简单随机样本,则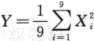服从_______分布,其自由度为_______.


    答案：
    解析：
    因为X～N(0，3)(i=1，2，…，9)，所以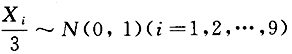且相互独立，故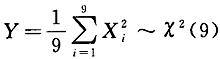，自由度为9.

  • 第6题：

    已知总体服从方差为25的正态分布，样本容量为100，样本均值为165，则总体均值95.45%（Z0.025=2）的置信区间是（）。

    A．164-166
    B．163-167
    C．162-168
    D．161-169

    答案：A
    解析：

  • 第7题：

    设总体X～N(u，σ2），基于来自总体X的容量为16的简单随机样本，测得样本均值图.png= 31.645，样本方差S2=0.09，则总体均值μ的置信度为0.98的置信区间为()。




    A.(30.88, 32.63)

    B.(31.45, 31.84)

    C.(31.62, 31.97)

    D.(30.45, 31.74)

    答案：B
    解析：

  • 第8题：

    设总体X~N(0,σ2)，X1，X2，...Xn是自总体的样本，则σ2的矩估计是:


    答案：D
    解析：
    提示 注意 E(x)=0，σ2=D(x)=E(x2) - [E(x)]2=E(x2)，σ2也是x的二阶原点矩，σ2的矩估计量是样本的二阶原点矩。

  • 第9题：

    若其他条件不变，置信度越高，则置信区间的长度（）。


    正确答案:越长

  • 第10题：

    设总体服从正态分布，方差未知，在样本容量和置信度保持不变的情形下，根据不同的样本值得到总体均值的置信区间长度将（）。

    • A、增加
    • B、不变
    • C、减少
    • D、都有可能

    正确答案:D

  • 第11题：

    多选题
    使用同一组样本根据正态分布估计总体均值时，如果将置信度由95%调整为90%，则（　　）。[2014年初级真题]
    A

    zα/2将增大

    B

    zα/2将减小

    C

    样本均值保持不变

    D

    置信区间宽度减小

    E

    置信区间宽度增加


    正确答案： D,A
    解析：
    zα/2为标准正态分布的α/2左分位数，随α的增大而减小，置信度由95%调整为90%时，α由0.05增大为0.1，zα/2减小。样本均值不受置信度变化的影响。置信度降低，说明置信区间的准确性降低，置信区间的宽度减小。

  • 第12题：

    单选题
    从一个服从正态分布的总体中随机抽取样本容量为n的样本，在95%的置信度下对总体参数进行估计的结果为：20±0.08。如果其他条件不变，样本量扩大到原来的4倍，则总体参数的置信区间应该是（    ）。
    A

    20±0.16

    B

    20±0.04

    C

    80±0.16

    D

    80±0.04


    正确答案： A
    解析：

  • 第13题：

    下面情况中,不适合用Z值检验两个独立样本平均数间差异的是( )

    A.总体方差已知且不等，n1和n2都是小样本容量

    B.总体方差未知且相等，n1和n2都是大样本容量

    C.总体方差未知且不等，n1和n2都是大样本容量

    D.总体方差未知且相等，n1和n2都是小样本容量


    参考答案：D

  • 第14题：

    已知总体服从正态分布，且总体标准差σ，从总体中抽取样本容量为n的产品，测得其样本均值为x，在置信水平为1-a=95%下，总体均值的置信区间为( )


    正确答案：A

  • 第15题：

    设总体X～N（μ,σ^2）,其中σ^2未知,^2s=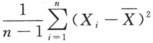,样本容量n,则参数μ的置信度为1－a的置信区间为().



    答案：D
    解析：
    因为σ^2未知，所以选用统计量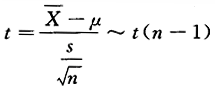，故μ的置信度为1-α的置信区间为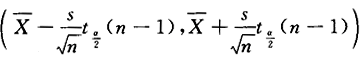，选(D).

  • 第16题：

    设X～N（μ,σ^2）,其中σ^2已知,μ为未知参数,从总体X中抽取容量为16的简单随机样本,且μ的置信度为0.95的置信区间中的最小长度为0.588,则σ^2=_______.


    答案：1、0.36
    解析：
    在σ^2已知的情况下，μ的置信区间为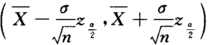，其中.于是有.

  • 第17题：

    设总体X～N(u，σ2），基于来自总体X的容量为16的简单随机样本，测得样本均值x= 31.645，样本方差S2=0.09，则总体均值μ的置信度为0.98的置信区间为( )。




    A.(30.88, 32.63)

    B.(31.45, 31.84)

    C.(31.62, 31.97)

    D.(30.45, 31.74)

    答案：B
    解析：

  • 第18题：

    从一个服从正态分布的总体中随机抽取样本容量为n的样本，在95％的置信度下对总体均值进行估计的结果为20±0.08。如果其他条件不变，样本容量扩大到原来的4倍，则总体均值的置信区间应该是( )。


    A.20±0.16

    B.20±0.04

    C.80±0.16

    D.80±0.04

    答案：B
    解析：

  • 第19题：

    从一个服从正态分布的总体中随机抽取样本容量为 n 的样本，在 95％的置信度下对总体均值进行估计的结果为 20±0.08。如果其他条件不变，样本容量扩大到原来的 4 倍，总体均值的置信区间应该是( )。


    A.20±0.16

    B.20±0.04

    C.80±0.16

    D.80±0.04

    答案：B
    解析：
    在正态分布下，总体均值区间估计为

    故样本容量扩大到原来的 4 倍，误差项变为原来的一半。

  • 第20题：

    在估计某一总体均值时，随机抽取n个单元作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是样本容量太小。


    正确答案:正确

  • 第21题：

    当总体方差已知，无论样本容量n的大小如何，进行正态总体均值的区间估计应采用的临界值为（）

    • A、F值
    • B、Z值
    • C、T值
    • D、x2值

    正确答案:B

  • 第22题：

    在估计某一总体均值时，随机抽取n个单位作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是（）

    • A、样本容量太小
    • B、估计量缺乏有效性
    • C、选择的估计量有偏
    • D、抽取样本时破坏了随机性

    正确答案:A

  • 第23题：

    判断题
    在估计某一总体均值时，随机抽取n个单元作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是样本容量太小。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

相关内容