,求正交矩阵T,使为对角矩阵.
题目
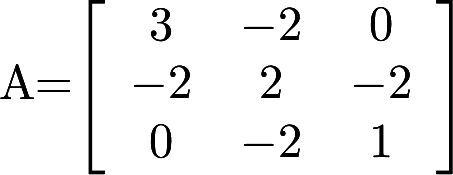 ,求正交矩阵T,使
,求正交矩阵T,使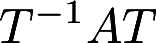 为对角矩阵.
为对角矩阵.相似考题
更多“,求正交矩阵T,使为对角矩阵.”相关问题
-
第1题:
设A为n阶实对称矩阵,下列结论不正确的是().A.矩阵A与单位矩阵E合同
B.矩阵A的特征值都是实数
C.存在可逆矩阵P,使P^-1AP为对角阵
D.存在正交阵Q,使Q^TAQ为对角阵答案:A解析:根据实对称矩阵的性质,显然(B)、(C)、(D)都是正确的,但实对称矩阵不一定是正定矩阵,所以A不一定与单位矩阵合同,选(A). -
第2题:
 ,求正交矩阵T,使
,求正交矩阵T,使 为对角矩阵.答案:解析:
为对角矩阵.答案:解析:

-
第3题:
试求一个正交的相似变换矩阵, 将对称阵 化为对角阵答案:解析:
化为对角阵答案:解析:
-
第4题:
设二次型
 (b>0),
(b>0),
其中二次型的矩阵A的特征值之和为1,特征值之积为-12.
(1)求a,b的值;
(2)利用正交变换将二次型f化为标准形,并写出所用的正交变换和对应的正交矩阵.答案:解析:
-
第5题:
设矩阵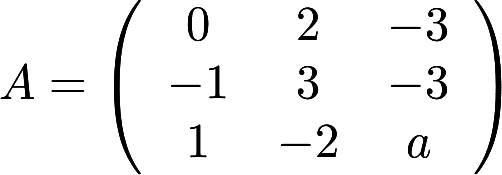 相似于矩阵
相似于矩阵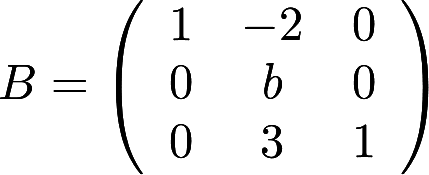 . (1)求a,b的值;(2)求可逆矩阵P,使
. (1)求a,b的值;(2)求可逆矩阵P,使 为对角阵答案:解析:
为对角阵答案:解析:
-
第6题:
设n阶矩阵A 满足 ,其中s≠t,证明A可对角化答案:解析:
,其中s≠t,证明A可对角化答案:解析:
-
第7题:
设Y~ ,A=
,A=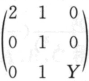 ,求矩阵A可对角化的概率.答案:解析:
,求矩阵A可对角化的概率.答案:解析:
-
第8题:
设A=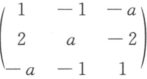 ,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.答案:解析:
,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.答案:解析:
-
第9题:
设A与B都是n阶正交矩阵,证明AB也是正交矩阵.答案:解析: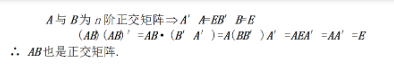
-
第10题:
三阶矩阵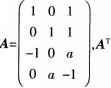 为矩阵A的转置,已知r(ATA)=2,且二次型
为矩阵A的转置,已知r(ATA)=2,且二次型
(1)求a;
(2)求二次型对应的二次矩阵,并将二次型化为标准型,写出正交变换过程。答案:解析:(1)由r(ATA)=r(A)=2可得, (2)
(2)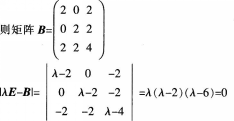

-
第11题:
若A,B是正交矩阵,则下列说法错误的是()。
- A、AB为正交矩阵
- B、A+B为正交矩阵
- C、ATB为正交矩阵
- D、AB-1为正交矩阵
正确答案:B -
第12题:
问答题设A为4阶魔术矩阵,分别对A进行如下操作: 求矩阵A的逆; 求矩阵A的行列式; 求矩阵A的秩; 求矩阵A的迹;正确答案: >>A=magic(4)
>>B=inv(A)
>>C=det(A)
>>D=rank(A)
>>E=trace(A)解析: 暂无解析 -
第13题:
设矩阵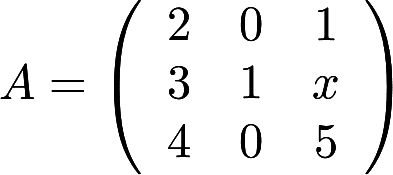 可相似对角化,求x答案:解析:
可相似对角化,求x答案:解析:
-
第14题:
已知 ,求作可s逆矩阵P,使得
,求作可s逆矩阵P,使得 是对角矩阵。答案:解析:
是对角矩阵。答案:解析:
-
第15题:
设3阶实对称矩阵A的各行元素之和都为3,向量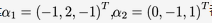 都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵
都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵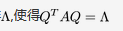 答案:解析:
答案:解析:
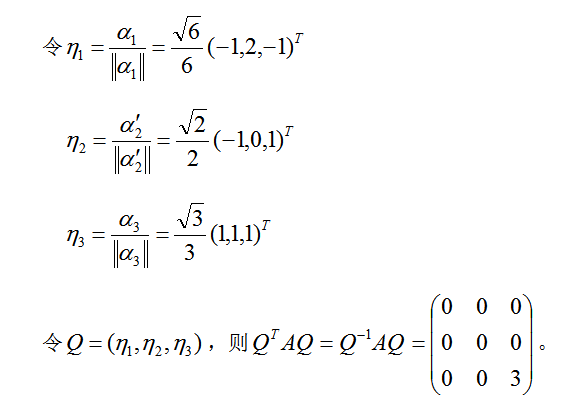
-
第16题:
设A为n×1矩阵,矩阵 .试证B为对称矩阵.如果A=(1,-1,2)T,求B.答案:解析:
.试证B为对称矩阵.如果A=(1,-1,2)T,求B.答案:解析: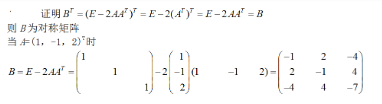
-
第17题:
已知二次型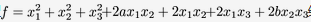 经过正交变换化为标准型
经过正交变换化为标准型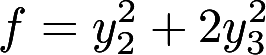 ,求参数a,b及所用的正交变换矩阵答案:解析:
,求参数a,b及所用的正交变换矩阵答案:解析:


-
第18题:
设矩阵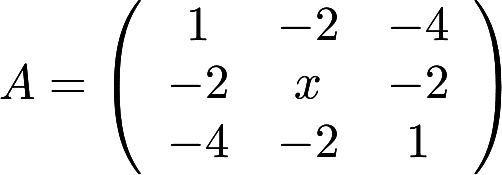 与
与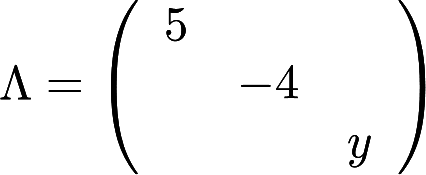 相似,求x, y,并求一个正交阵P,使
相似,求x, y,并求一个正交阵P,使 。答案:解析:
。答案:解析:
-
第19题:
判断矩阵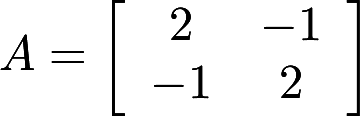 是否可对角化?若可对角化,求可逆矩阵使之对角化。答案:解析:
是否可对角化?若可对角化,求可逆矩阵使之对角化。答案:解析:
-
第20题:
设矩阵A=
(1)已知A的一个特征值为3,试求y;
(2)求可逆矩阵P,使(AP)^T(AP)为对角矩阵.答案:解析:
-
第21题:
已知二次型f(x1,x2,3x)=x^TAx在正交变换x=Qy下的标准形为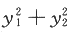 ,且Q的第3列为
,且Q的第3列为 .
.
(Ⅰ)求矩阵A;
(Ⅱ)证明A+E为正定矩阵,其中E为三阶单位矩阵.答案:解析:
-
第22题:
若A,口是正交矩阵,则下列说法错误的是( )。A、AB为正交矩阵
B、A+B为正交矩阵
C、A-1B为正交矩阵
D、AB-1为正交矩阵答案:B解析: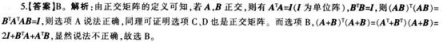
-
第23题:
设A为4阶魔术矩阵,分别对A进行如下操作: 求矩阵A的逆; 求矩阵A的行列式; 求矩阵A的秩; 求矩阵A的迹;
正确答案: >>A=magic(4)
>>B=inv(A)
>>C=det(A)
>>D=rank(A)
>>E=trace(A) -
第24题:
单选题若A,B是正交矩阵,则下列说法错误的是()。AAB为正交矩阵
BA+B为正交矩阵
CATB为正交矩阵
DAB-1为正交矩阵
正确答案: A解析: 由正交矩阵的定义可知,若A,B正交,则有ATA=I(I为单位阵),BTB=I,则(AB)T(AB)=BTATAB=I,则选项A正确,同理可证明选项C、D也是正交矩阵。而选项B,(A+B)T(A+B)=(AT+BT)(A+B)=2I+BTA+ATB,显然不正确,故选B。
