设随机变量X服从参数为2的指数分布,令U=,V=:求：(1)(U,V)的分布；(2)U,V的相关系数.

题目
设随机变量X服从参数为2的指数分布,令U=,V=:
　　求：(1)(U,V)的分布；(2)U,V的相关系数.

相似考题

1.设随机变量X与Y相互独立且都服从参数为A的指数分布,则下列随机变量中服从参数为2λ的指数分布的是().A.X+y B.X-Y C.max{X,Y} D.min{X,Y}

2.设总体X服从参数λ的指数分布，X1，X2，…，Xn是从中抽取的样本，则E(X)为( )。

3.设随机变量X1,X2,…,Xn相互独立且在［0,na］上服从均匀分布,令U=max{X1,X2,…,Xn},求U的数学期望与方差.

4.设X1，X2，…，Xn，…为独立同分布的随机变量列，且均服从参数为λ(λ>1)的指数分布，记φ(x)为标准正态分布函数，则

更多“设随机变量X服从参数为2的指数分布,令U=,V=: ”相关问题

  • 第1题：

    设随机变量X服从参数为A的指数分布,则P{X>)=_______.


    答案：
    解析：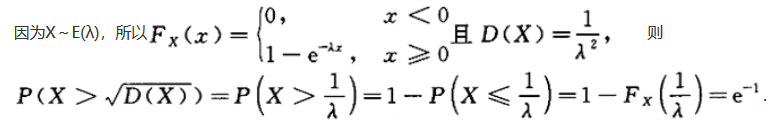

  • 第2题：

    随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为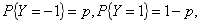令Z=XY。p为何值时，X与Z不相关


    答案：
    解析：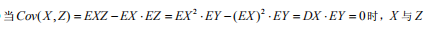

  • 第3题：

    设随机变量X服从参数为λ的指数分布，则=_______.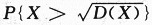


    答案：
    解析：
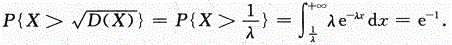    答案应填e.

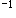
  • 第4题：

    设随机变量X服从参数为2的泊松分布,令Y=4X-3,则E(Y)=_______,D(Y)=_______.


    答案：1、32
    解析：
    因为X～P(2)，所以E(X)=D(X)=2，于是E(Y)=4E(X)-3=5，D(Y)=16D(X)=32.

  • 第5题：

    设随机变量X,Y相互独立且都服从标准正态分布,令U=X^2+Y^2.求：
    　　(1）(u);(2)P{U>D(U)｜U>E(U)}.


    答案：
    解析：

  • 第6题：

    设随机变量(X,Y)在区域D={(z,y)｜0≤x≤2,0≤y≤1}上服从均匀分布,令
    　　U=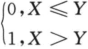,V=.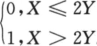
    　　(1)求(U,V)的联合分布；(2)求.


    答案：
    解析：

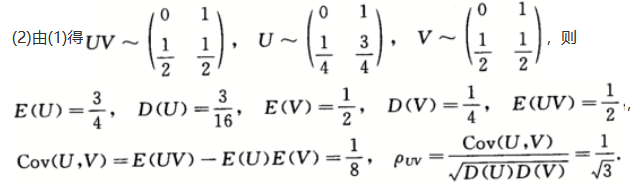
  • 第7题：

    设随机变量X服从参数为1的泊松分布,则P{X=EX^2}=________.


    答案：
    解析：
    X～P(λ)，则有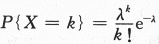，k=0，1，2，…且E(X)=λ，D(X)=λ，现λ=1，直接代入即可.
    【求解】E(X^2)=D(X)+［E(X)］^2=1+1=2，所以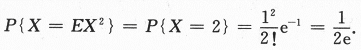

  • 第8题：

    设随机变量X服从参数为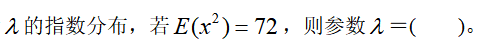



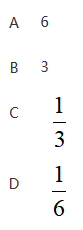    答案：D
    解析：
    本题考查指数分布的数字特征与参数之间的关系。X服从参数为的指数分布，



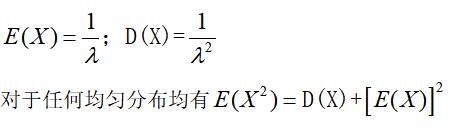
    依此原理计算。

  • 第9题：

    设随机变量Y服从参数为1的指数分布，a为常数且大于零，则P{Y≤a+1|Y>a}=（）


    正确答案:1-e-1

  • 第10题：

    设随机变量X服从参数为2的指数分布，则E（2X－1）=（）

    • A、0
    • B、1
    • C、3
    • D、4

    正确答案:A

  • 第11题：

    设随机变量X服从参数为2，p的二项分布，随机变量Y服从参数为3，p的二项分布，若P{X≥1}=5/9，则P{Y≥1}=（）。


    正确答案:19/27

  • 第12题：

    单选题
    设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。
    A

    1

    B

    3


    正确答案： D
    解析： 暂无解析

  • 第13题：

    随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为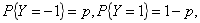令Z=XY。X与Z是否相互独立


    答案：
    解析：
    因为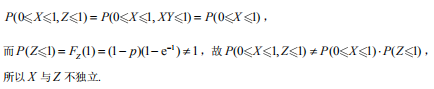

  • 第14题：

    设随机变量X服从参数为的指数分布,对X独立地重复观察4次,用Y表示观察值大于3的次数,求E(Y^2).


    答案：
    解析：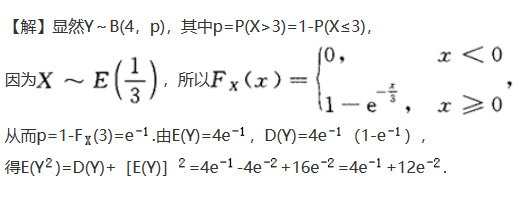

  • 第15题：

    设随机变量X服从参数为λ的指数分布,且E［（X-1）(X+2)］=8,则λ=_______.


    答案：
    解析：
    由随机变量X服从参数为λ的指数分布，得，于是，而，解得λ=.

  • 第16题：

    设随机变量X,Y相互独立,D(X)=4D(Y),令U=3X+2Y,V=3X-2Y,则=_______.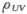


    答案：
    解析：
    Cov(U，V)=Cov(3X+2Y，3X-2Y)=9Cov(X，X)-4Cov(Y，Y)=9D(X)-4D(Y)=32D(Y)，由X，Y独立，得D(U)=D(3X+2Y)=9D(X)+4D(Y)=40D(Y)，D(V)=D(3X-2Y)=9D(X)+4D(Y)=40D(Y)，
    所以

  • 第17题：

    设随机变量X服从参数为2的指数分布,证明：Y=1-在区间(0,1)上服从均匀分布.


    答案：
    解析：

  • 第18题：

    设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3.
    　　设随机变量U=max{X,Y},V=min{X,Y}.
    　　(1)求二维随机变量(U,V)的联合分布；(2)求Z=UV的分布；
    　　(3)判断U,V是否相互独立？(4)求P（U=V）.


    答案：
    解析：

  • 第19题：

    设随机变量X与Y相互独立，且分别服从参数为1与参数为4的指数分布，则P{X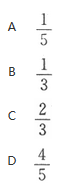


    答案：A
    解析：
    X～E(1)，Y～E(4)且相互独立，所以(X，Y)的概率密度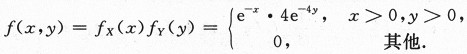　　
    　　利用公式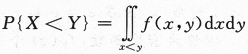可以计算出结果.
    　　【求解】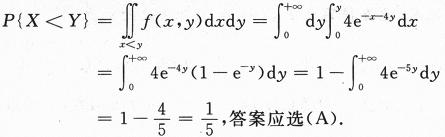

  • 第20题：

    设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。

    • A、1
    • B、3

    正确答案:D

  • 第21题：

    设随机变量X服从参数为2的泊松分布，且Y=3X-2，则E（Y）=（）。


    正确答案:4

  • 第22题：

    设随机变量X服从参数为2的泊松分布，则E（2X）=（）


    正确答案:4

  • 第23题：

    问答题
    X服从参数为2的指数分布，Y服从参数为4的指数分布，则E(2X2+3Y)=____ .

    正确答案：
    解析：

相关内容