设随机变量X～N（μ,σ^2）,且方程x^2+4r+X=0无实根的概率为,则μ=_______.

题目
设随机变量X～N（μ,σ^2）,且方程x^2+4r+X=0无实根的概率为,则μ=_______.

相似考题

1.设随机变量X~N(μ,б2),且P(X≤c)=P(X>c),则c=()。A、0B、μC、-μD、б

2.设随机变量X～U［1,7］,则方程x^2+2Xx+9=0有实根的概率为().

3.设随机变量X,Y相互独立,且X～N,Y～N,则与Z=Y-X同分布的随机变量是().A.X-Y B.X+Y C.X-2Y D.Y-2X

4.设随机变量X~N(μ,б2),且P(X≤c),则c=()。A、0B、μC、-μD、б

更多“设随机变量X～N（μ,σ^2）,且方程x^2+4r+X=0无实根的概率为,则μ=_______.”相关问题

  • 第1题：

    设随机变量X,Y相互独立,且X～N(0,1),Y～N(1,1),则().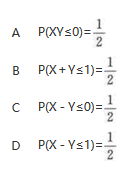


    答案：B
    解析：
    X，Y独立，X～N(0，1)，Y～N(1，1)，X+Y～N(1，2)P(X+Y≤1)=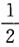，所以选(B).

  • 第2题：

    设随机变量X~N(0，σ2)，则对于任何实数λ，都有：
    A. P(X≤λ)=P(X≥λ)
    B.P(X≥λ)=P(X≤-λ)
    C.X-λ~N(λ,σ2-λ2)
    D.λX~N(0,λσ2)


    答案：B
    解析：

    Y=aX+b~N(au+b,a2σ2)，或利用u=0时概率密度f(x)曲线的对称性，概率(积分值)与曲边梯形面积对应判断。

  • 第3题：

    设随机变量X服从正态分布N(μ，σ^2)，(σ>0)且二次方程y^2+4y+X=0无实根的概率为，则μ=________.


    答案：1、4
    解析：
    二次方程无实根，即y^2+4y+X=0的判别式16-4X<0.其概率为，即P{X>4}=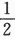，所以μ=4，答案应填4.

  • 第4题：

    设随机变量X～N(0,1),且y=9X^2,则y的密度函数为_______.


    答案：
    解析：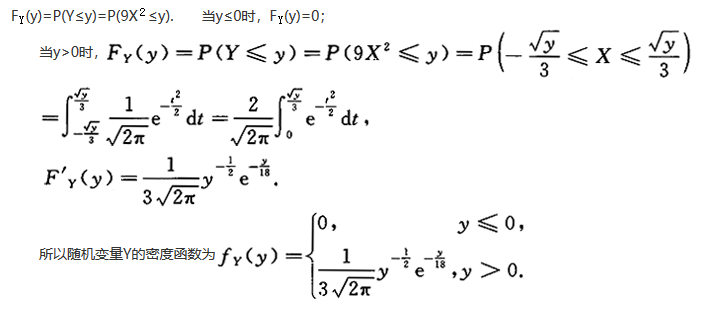

  • 第5题：

    设随机变量X,Y相互独立,且X～N(0,4),Y的分布律为Y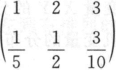～.则P(X-1-2Y≤4)=_______.


    答案：1、0.46587
    解析：
    p(X+2Y≤4)=P(Y=1)P(X≤4-2Y｜Y=1)+P(Y=2)P(X≤4-2Y｜Y=2)+P(Y=3)P(X≤4-2Y｜Y=3)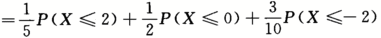

  • 第6题：

    设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=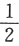.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为

    A.A0
    B.1
    C.2
    D.3

    答案：D
    解析：

  • 第7题：

    设随机变量X服从N（0，2），则（ ）。



    答案：D
    解析：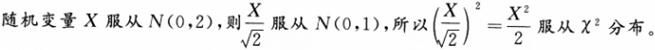

  • 第8题：

    设随机变量X与Y相互独立，且X~N（1，2），Y~N（0，1）。令Z=-Y+2X+3，则D（Z）=（）。


    正确答案:9

  • 第9题：

    单选题
    设随机变量X～N（3，22），且P（X＞a）＝P（X＜a），则常数a为（　　）。
    A

    0

    B

    2

    C

    3

    D

    4


    正确答案： C
    解析：
    由于X为连续型随机变量，所以P（X＝a）＝0，已知P（X＞a）＝P（X＜a），可得P（X＜a）＝P（X＞a）＝0.5，即a处在正态分布的中心位置，根据题干中的条件可知该分布关于m＝3轴对称，所以a＝3。

  • 第10题：

    单选题
    设f（x）＝x（x－1）（x－2），则方程f′（x）＝0的实根个数是（　　）。[2016年真题]
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： C
    解析：
    先对方程求导，得：f′（x）＝3x2－6x＋2，再根据二元函数的判别式Δ＝b2－4ac＝12＞0，可知方程有两个实根。

  • 第11题：

    问答题
    已知p：方程x2+mx+1=0有两个不等负实根。q：方程4x2+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。

    正确答案： 因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
    （1）若p为真，则q为假。
    p为真，方程x2+mx+1=0有两个不等负实根成立，即△=m2-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
    q为假，方程4x2+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）2-16≥0，所以m≥3或m≤1。
    取交集得到，m≥3：
    （2）若q为真，则p为假。
    q为真，即方程4x2+4（m-2）x+1=0无实根成立，即△=16（m-2）2-16<0，所以1p为假，方程x2+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m2-4≤0，或②有两个不等正实根，△=m2-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
    取交集得到：1综上所述m≥3或1
    解析： 暂无解析

  • 第12题：

    单选题
    设f(x)=x(x-1)（x-2），则方程f'(x)=0的实根个数是：
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： A
    解析：

  • 第13题：

    设f（x）=x（x-1）（x-2），则方程



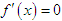
    的实根个数是（　　）。

    A、 3
    B、 2
    C、 1
    D、 0

    答案：B
    解析：
    先对方程求导，得：



    再根据二元函数的判别式



    判断可知方程有两个实根。

  • 第14题：

    设随机变量X?N(0，σ2)，则对于任何实数λ都有:
    (A) P(X≤λ)=P(X≥λ)(B)P(X≥λ)= P(X≤-λ)
    (C) X-λ~N(λ，σ2-λ2)(D)λX~N(0，λσ2)


    答案：B
    解析：
    解:选B。
    排除错误选项。
    X-λ~N(-λ，σ2)，选项C错误。
    λX~N(0，λ2σ2)，选项D错误。

  • 第15题：

    设随机变量X～B（n,p）,且E(X)=5,E(X^2)=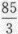,则n=_______,p=_______.


    答案：
    解析：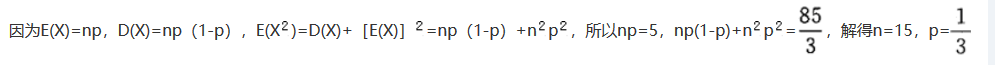

  • 第16题：

    设随机变量X～N(0,σ^2),Y～N(0,4σ^2),且P(X≤1,y≤-2)=,则P（X>1,Y>-2）=_______.


    答案：
    解析：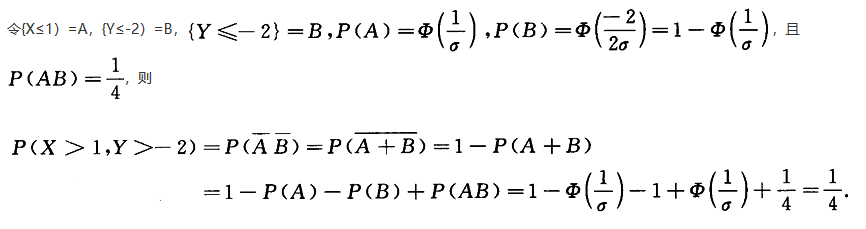

  • 第17题：

    设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.


    答案：
    解析：
    由X～N(1，2)，Y～N(-1，2)，Z～N(0，9)，得X+Y～N(0，4)，且，故.

  • 第18题：

    设随机变量X,Y相互独立，且X的概率分布为P{X=0)=P{X=2)=，Y的概率密度为
    　　(Ⅰ)求P{Y≤EY}；
    　　(Ⅱ)求Z=X+Y的概率密度.


    答案：
    解析：

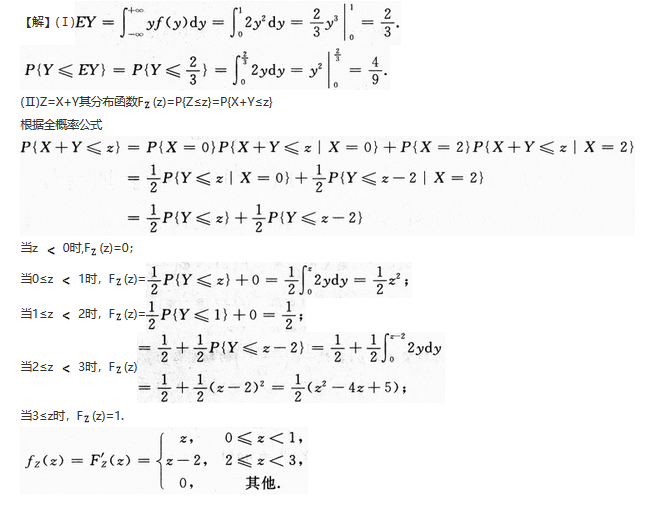
  • 第19题：

    已知p：方程x2+mx+1=0有两个不等负实根。q：方程4x2+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。


    正确答案: 因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
    （1）若p为真，则q为假。
    p为真，方程x2+mx+1=0有两个不等负实根成立，即△=m2-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
    q为假，方程4x2+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）2-16≥0，所以m≥3或m≤1。
    取交集得到，m≥3：
    （2）若q为真，则p为假。
    q为真，即方程4x2+4（m-2）x+1=0无实根成立，即△=16（m-2）2-16<0，所以1p为假，方程x2+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m2-4≤0，或②有两个不等正实根，△=m2-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
    取交集得到：1综上所述m≥3或1

  • 第20题：

    设随机变量X服从正态分布U（μ，σ2）（σ>0），且二次方程y2+4y+X=0无实根的概率为1/2，则μ=（）


    正确答案:4

  • 第21题：

    单选题
    设随机变量X～N（3，22），且P（X＞a）＝P（X＜a），则常数a为（　　）。[2016年5月真题]
    A

    0

    B

    2

    C

    3

    D

    4


    正确答案： C
    解析：
    由于X为连续型随机变量，所以P（X＝a）＝0，已知P（X＞a）＝P（X＜a），可得P（X＜a）＝P（X＞a）＝0.5，即a处在正态分布的中心位置，根据题干中的条件可知该分布关于m＝3轴对称，所以a＝3。

  • 第22题：

    填空题
    设随机变量X服从正态分布N（μ，σ2）（σ＞0），且二次方程y2＋4y＋X＝0无实根的概率为0.5，则μ＝____。

    正确答案： 4
    解析：
    令Y＝（X－μ）/σ，则Y服从标准正态分布N（0，1）。
    该二次方程无实根的充要条件为4－X＜0，根据题意，有：
    0.5＝P{X＞4}＝1－P{X≤4}＝1－P{（X－μ）/σ≤（4－μ）/σ}＝1－P{Y≤（4－μ）/σ}＝1－Φ[（4－μ）/σ]，即Φ[（4－μ）/σ]＝0.5，故（4－μ）/σ＝0，μ＝4。

  • 第23题：

    单选题
    设随机变量X服从正态分布N（μ，σ2）（σ＞0），且二次方程y2＋4y＋X＝0无实根的概率为0.5，则μ＝（　　）。
    A

    1

    B

    2

    C

    4

    D

    5


    正确答案： A
    解析：
    令Y＝（X－μ）/σ，则Y服从标准正态分布N（0，1）。
    该二次方程无实根的充要条件为4－X＜0，根据题意，有：
    0.5＝P{X＞4}＝1－P{X≤4}＝1－P{（X－μ）/σ≤（4－μ）/σ}＝1－P{Y≤（4－μ）/σ}＝1－Φ[（4－μ）/σ]，即Φ[（4－μ）/σ]＝0.5，故（4－μ）/σ＝0，μ＝4。

相关内容