用消元法解方程组

题目
用消元法解方程组

相似考题

1.设n元齐次线性方程组AX=O只有零解,则秩(A)=()。

2.通常把按照先消元、后回代两个步骤求解线性方程组的方法称为高斯(Gauss)消去法。()

3.用列主元消元法解线性方程组x1＋2x2＋x3=02x1＋2x2＋3x＋=3－x1－3x2=2作一次消元后得到的第三个方程为()A、-x2+x3=2B、-2x2+1.5x3=3.5C、-2x2+x3=3D、x2-0.5x3=-1.5

4.用迭代法解线性方程组时，迭代能否收敛与初始向量的选择、系数矩阵及其演变方式有关，与常数项无关。()

更多“用消元法解方程组”相关问题

  • 第1题：

    解线性方程组的主元素消去法中选择主元的目的是()

    A、控制舍入误差

    B、减少方法误差

    C、防止计算时溢出

    D、简化计算


    参考答案：A

  • 第2题：

    用列主元消去法解线性方程组,

    A、3

    B、4

    C、-4

    D、9


    参考答案：C

  • 第3题：

    讨论方程组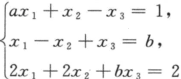的解的情况,在方程组有解时求出其解,其中a,b为常数.


    答案：
    解析：

  • 第4题：

    用克拉默法则解线性方程组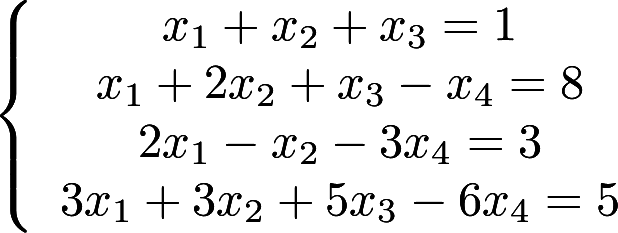


    答案：
    解析：

  • 第5题：

    设(Ⅰ)和(Ⅱ)都是3元非齐次方程组,(Ⅰ)有通解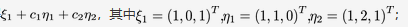；(Ⅱ)有通解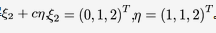。求(Ⅰ)和(Ⅱ) 的公共解


    答案：
    解析：

  • 第6题：

    已知齐次线性方程组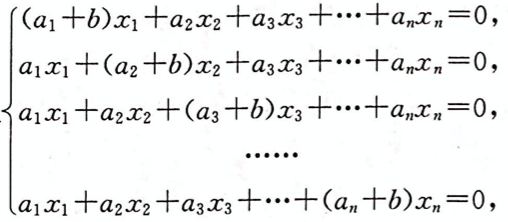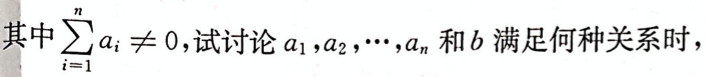（1）方程组仅有零解；（2）方程组有非零解，在有非零解时，求此方程组的一个基础解系.


    答案：
    解析：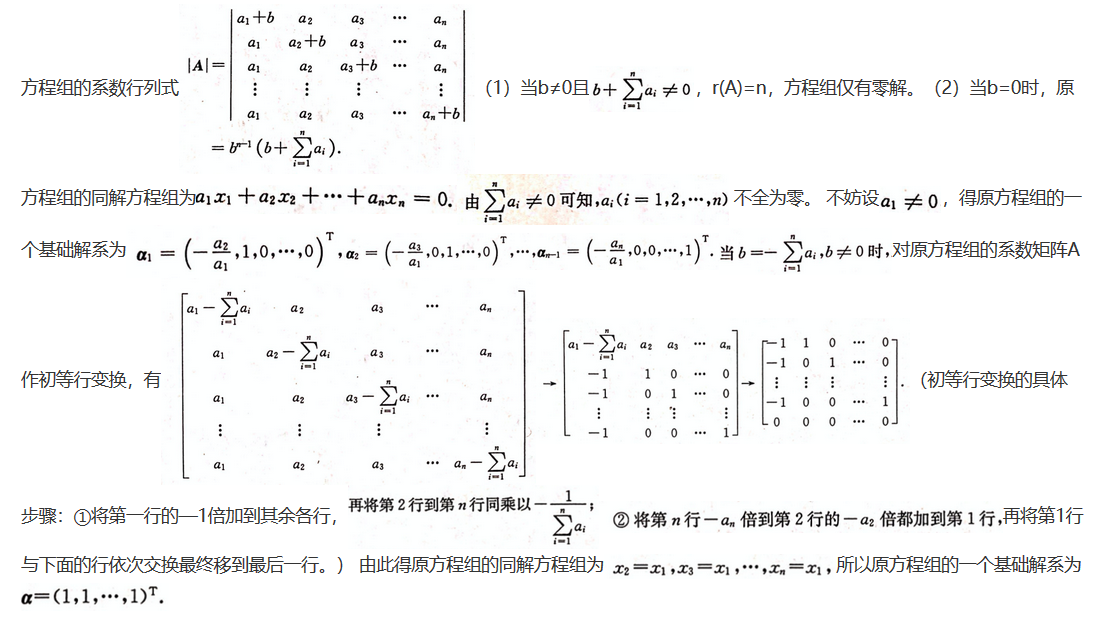

  • 第7题：

    求齐次线性方程组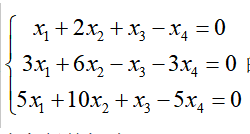的全部解（要求用基础解系表示）。


    答案：
    解析：
    解：本题考查齐次线性方程组的解法。

  • 第8题：

    应用哈代—克罗斯法解环方程组的步骤怎样？


    正确答案: 应用哈代—克罗斯法解环方程组的步骤：
    1）根据城镇的供水情况，拟定环状网各管段的水流方向，得出初步分配流量；
    2）由初分流量计算各管段的摩阻系数和水头损失；
    3）假定各环水流顺时针方向管段中的水头损失为正，逆时针方向管段中的水头损失为负，计算该环内各管段的水头损失代数和，如果代数和大于零，说明顺时针方向各管段中初分流量多了些，逆时针方向各管段中初分流量少了些，如果代数和小于零，说明逆时针方向各管段中初分流量多了些，顺时针方向各管段中初分流量少了些；
    4）求出校正流量，如果闭和差为正，校正流量即为负，反之校正流量为正；
    5）利用校正流量调整各管段的流量，得到第一次校正的管段流量，按此流量再进行计算，如果闭和差尚未达到允许的精度，返回到第2步再进行计算，直到闭和差符合要求为止。

  • 第9题：

    紫外－可见分光光度法中多组分定量方法中，如果两组分吸收曲线重叠时候可以采用（）定量。

    • A、解二元一次联立方程组
    • B、解二元二次联立方程组
    • C、解一元二次联立方程组
    • D、解二元三次联立方程组

    正确答案:A

  • 第10题：

    问答题
    设AX=0与BX=0均为n元齐次线性方程组，秩r（A）=r（B），且方程组AX=0的解均为方程组BX=0的解，证明方程组AX=0与BX=0同解.

    正确答案：
    设r(A)=r(B)=r,方程组AX=0的基础解系为①:ζ1,ζ2,…,ζn-r,方程组BX=0的基础解系为②:η1,η2,…,ηn-r.
    构造向量组③:ζ1,ζ2,…,ζn-r,η1,η2,…,ηn-r.
    由向量组①可由②线性表示,则向量组②和③等价,从而r(③)=n-r,所以ζ1,ζ2,…,ζn-r是向量组③的极大线性无关组,有η1,η2,…,ηn-r可由ζ1,ζ2,…,ζn-r线性表示,即BX=0的任一解都可由ζ1,ζ2,…,ζn-r线性表示,故BX=0的解都是AX=0的解,所以方程组AX=0与BX=0同解.
    解析： 暂无解析

  • 第11题：

    单选题
    采用对流换热边界层微分方程组，积分方程组或雷诺类比法求解对流换热过程中，正确的说法是（  ）。
    A

    微分方程组的解是精确解

    B

    积分方程组的解是精确解

    C

    雷诺类比的解是精确解

    D

    以上三种均为近似值


    正确答案： D
    解析：

  • 第12题：

    填空题
    解线性方程组Ax=b的高斯顺序消元法满足的充要条件为（）。

    正确答案： A的各阶顺序主子式均不为零
    解析： 暂无解析

  • 第13题：

    用高斯顺序消去法解线性方程组，消元能进行到底的充分必要条件是线性方程组的系数矩阵的各阶顺序主子式均不为0()


    参考答案：√

  • 第14题：

    设A是m×n阶矩阵,下列命题正确的是().

    A.若方程组AX=0只有零解,则方程组AX=b有唯一解
    B.若方程组AX=0有非零解,则方程组AX=b有无穷多个解
    C.若方程组AX=b无解,则方程组AX=0一定有非零解
    D.若方程组AX=b有无穷多个解,则方程组AX=0一定有非零解

    答案：D
    解析：

  • 第15题：

    设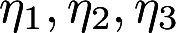为3个n维向量,已知n元齐次方程组AX=0的每个解都可以用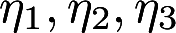线性表示,并且r(A)=n-3,证明{图2为AX=0的一个基础解系.}


    答案：
    解析：

  • 第16题：

    已知下列非齐次线性方程组(Ⅰ)，(Ⅱ)
    　　
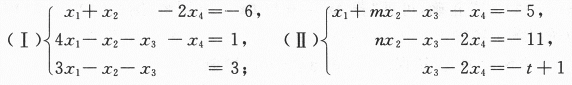
    　　(1)求解方程组(Ⅰ)，用其导出组的基础解系表示通解.
    　　(2)当方程组中的参数m，n，t为何值时，方程组(Ⅰ)与(Ⅱ)同解.


    答案：
    解析：

  • 第17题：

    采用对流换热边界层微分方程组、积分方程组或雷诺类比法求解，对流换热过程中，正确的说法是（　　）。

    A． 微分方程组的解是精确解
    B． 积分方程组的解是精确解
    C． 雷诺类比的解是精确解
    D． 以上三种均为近似解

    答案：A
    解析：
    对流换热的求解方法包括分析法、类比法和实验法。分析法包括微分方程组求解和积分方程组求解。在所有方法中，只有微分方程组的解是精确解；积分方程组的求解要先假设速度和温度的分布，因此是近似解；雷诺类比的解是由比拟理论求得的，也是近似解。

  • 第18题：

    《代入法解二元一次方程组》
    一、面试考题
    试讲题目
    1.题目：代入法解二元一次方程组
    2.内容：

    3.基本要求：
    (1)试讲时间10分钟以内;
    (2)讲解要目的明确、条理清楚、重点突出;
    (3)根据讲解的需要适当板书;
    (4)结合例子归纳代入法解二元一次方程组的思路及步骤。
    答辩题目
    1.二元一次方程组有哪些解法?
    2.你是如何引导学生掌握二元一次方程组的解法的?
    注：图片节选自北京师范大学出版社初中数学八年级上册第109页


    答案：
    解析：
    二、考题解析
    【教学过程】

    (四)小结作业
    小结：重点回顾代入法解二元一次方程组的基本思路及步骤。
    作业：思考练习题中的两个方程组是否有其他的求解方法。
    【板书设计】

  • 第19题：

    解线性方程组Ax=b的高斯顺序消元法满足的充要条件为（）。


    正确答案:A的各阶顺序主子式均不为零

  • 第20题：

    高斯消元法是（）直接解法中的一种较为优秀的一种。

    • A、矩阵
    • B、线性方程组
    • C、LU分解
    • D、支路电流法

    正确答案:B

  • 第21题：

    单选题
    采用对流换热边界层微分方程组，积分方程组或雷诺类比法求解对流换热过程中，正确的说法是（　　）。[2010年真题]
    A

    微分方程组的解是精确解

    B

    积分方程组的解是精确解

    C

    雷诺类比的解是精确解

    D

    以上三种均为近似值


    正确答案： A
    解析：
    对流换热的求解方法包括分析法、类比法和实验法。分析法包括微分方程组求解和积分方程组求解。在所有方法中，只有微分方程组的解是精确解；积分方程组的求解要先假设速度和温度的分布，因此是近似解；雷诺类比的解是由比拟理论求得的，也是近似解。

  • 第22题：

    问答题
    应用哈代—克罗斯法解环方程组的步骤怎样？

    正确答案： 应用哈代—克罗斯法解环方程组的步骤：
    1）根据城镇的供水情况，拟定环状网各管段的水流方向，得出初步分配流量；
    2）由初分流量计算各管段的摩阻系数和水头损失；
    3）假定各环水流顺时针方向管段中的水头损失为正，逆时针方向管段中的水头损失为负，计算该环内各管段的水头损失代数和，如果代数和大于零，说明顺时针方向各管段中初分流量多了些，逆时针方向各管段中初分流量少了些，如果代数和小于零，说明逆时针方向各管段中初分流量多了些，顺时针方向各管段中初分流量少了些；
    4）求出校正流量，如果闭和差为正，校正流量即为负，反之校正流量为正；
    5）利用校正流量调整各管段的流量，得到第一次校正的管段流量，按此流量再进行计算，如果闭和差尚未达到允许的精度，返回到第2步再进行计算，直到闭和差符合要求为止。
    解析： 暂无解析

  • 第23题：

    单选题
    用列主元消去法解线性方程组 ，第1次消元，选择主元为（） 。
    A

    -4

    B

    3

    C

    4

    D

    -9


    正确答案： A
    解析： 暂无解析

相关内容