设二次型f(x1,x2,x3)=（a>0）的秩为2.(1)求a;(2)用正交变换法化二次型为标准形.

题目
设二次型f(x1,x2,x3)=（a>0）的秩为2.(1)求a;(2)用正交变换法化二次型为标准形.

相似考题

1.设配对设计资料的变量值为X1和x2(无差值为0者)，则配对设计资料的符号秩和检验是A.分别按X1和X2从小到大编秩B.把X1和X2所有观察值混合从小到大编秩C.把X1和X2所有观察值混合按绝对值从小到大编秩D.把X1和X2的差值从小到大编秩E.把X1和X2的差值的绝对值从小到大编秩

2.二次型用正交变换化成的标准型为( )

3.方程组的解为( )。A、x1=-18，x2=0，x3=0 B、x1=0，x2=0，x3=3 C、x1=2，x2=1，x3=3 D、x1=0，x2=6，x3=0

4.设二次型要使f的秩为2，则参数t的值等于（　　）。 A．3 B．2 C．1 D．0

更多“设二次型f(x1,x2,x3)=（a>0）的秩为2.(1)求a;(2)用正交变换法化二次型为标准形.”相关问题

  • 第1题：

    设某元件的使用寿命X的概率密度为f(x；θ)=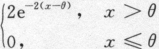,其中θ>0为未知参数,又设(x1,x2,…,xn)是样本(X1,X2,…,Xn)的观察值,求参数θ的最大似然估计值.


    答案：
    解析：

  • 第2题：

    求一个正交变换将二次型化成标准形


    答案：
    解析：

  • 第3题：

    已知二次型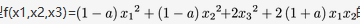的秩为2.(1)求a.(2)求作正交变换X=QY,把f(x1,x2,x3)化为标准形.(3)求方程f(x1,x2,x3)=0的解


    答案：
    解析：

  • 第4题：

    设二次型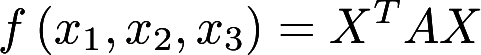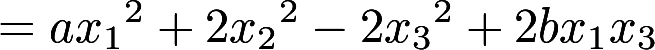,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化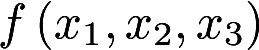为标准型


    答案：
    解析：

  • 第5题：

    设二次型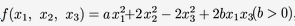其中二次型矩阵A的特征值之和为1, 特征值之积-12.(1) 求a,b的值; (2) 求一正交变换把二次型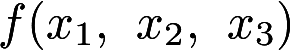化成标准型(需写出正交变换及标准型)


    答案：
    解析：

  • 第6题：

    假设把任意x1≠0，x2≠0，…，xn≠0代入二次型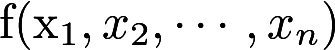都使f＞0，问f是否必然正定?


    答案：
    解析：

  • 第7题：

    设总体X的概率密度为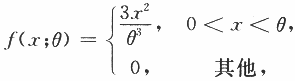其中θ∈(0,+∞)为未知参数，X1，X2，X3为来自总体X的简单随机样本，令T=max(X1，X2，X3).
    　　(Ⅰ)求T的概率密度；
    　　(Ⅱ)确定a，使得aT为θ的无偏估计.


    答案：
    解析：

  • 第8题：

    要使得二次型f(x1,x2 ,x3)=x12+2tx1x2+x22-2x1x3+2x2x3+2x32 为正定的，则t的取值条件是：

    A.-10 D.t

    答案：B
    解析：

  • 第9题：

    设二次型f(x1,x2,x3)在正交变换为x=py下的标准形为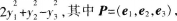
    若Q=(e1-e3，e2)，则f(x1,x2,x3)在正交变换x=Qy下的标准型为( )。
    A．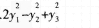
    B．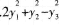
    C．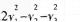
    D．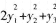


    答案：A
    解析：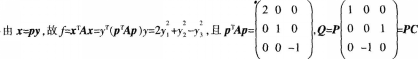

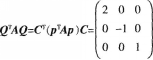
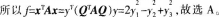
  • 第10题：

    设配对设计资料的变量值为X1和X2，则配对资料的秩和检验（）

    • A、分别按X1和X2从小到大编秩
    • B、把X1和X2综合从小到大编秩
    • C、把X1和X2综合按绝对值从小到大编秩
    • D、把X1和X2的差数从小到大编秩
    • E、把X1和X2的差数的绝对值从小到大编秩

    正确答案:E

  • 第11题：

    问答题
    设f（x）在[a，b]上连续，在（a，b）内可微，若a≥0，证明在（a，b）内存在三个数x1、x2、x3，使f′（x1）＝（b＋a）f′（x2）/（2x2）＝（b2＋ab＋a2）f′（x3）/（3x32）。

    正确答案：
    令g(x)=x2,当a≥0时,由于f(x)和g(x)在[a,b]上均连续,且在(a,b)上均可微,则由柯西中值定理得,必∃x2∈(a,b),使[f(b)-f(a)]/(b2-a2)=f′(x2)/(2x2),即[f(b)-f(a)]/(b-a)=(b+a)f′(x2)/(2x2)①
    令φ(x)=x3,当a≥0时,由于f(x)和φ(x)在[a,b]上均连续,且在(a,b)上均可微,则由柯西中值定理得,必∃x3∈(a,b),使[f(b)-f(a)]/(b3-a3)=f′(x3)/(3x32),即[f(b)-f(a)]/(b-a)=(b2+ab+a2)f′(x3)/(3x32)②
    由拉格朗日中值定理知,必∃x1∈(a,b),使[f(b)-f(a)]/(b-a)=f′(x1)③
    由①②③得f′(x1)=(b+a)f′(x2)/(2x2)=(b2+ab+a2)f′(x3)/(3x32)。
    解析： 暂无解析

  • 第12题：

    单选题
    二次型f（x1，x2，x3）=λx21+（λ-1）λ22+（λ2+1）x23，当满足（）时，是正定二次型。（）
    A

    λ>0

    B

    λ>-1

    C

    λ>1

    D

    以上选项均不成立


    正确答案： C
    解析： 暂无解析

  • 第13题：

    设二次型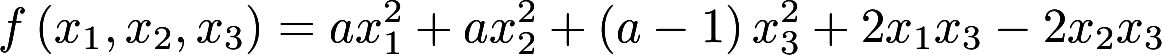. （Ⅰ）求二次型的矩阵的所有特征值； （Ⅱ）若二次型的规范形为，求的值


    答案：
    解析：

  • 第14题：

    设二次型
    　　(b>0),
    　　其中二次型的矩阵A的特征值之和为1，特征值之积为-12.
    　　(1)求a，b的值；
    　　(2)利用正交变换将二次型f化为标准形，并写出所用的正交变换和对应的正交矩阵.


    答案：
    解析：

  • 第15题：

    设n阶实对称矩阵A的秩为r，且满足，求 ①二次型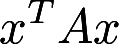的标准形； ②行列式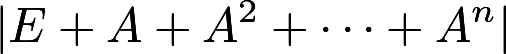的值，其中E为单位矩阵


    答案：
    解析：

  • 第16题：

    二次型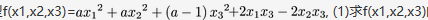, (1)求f(x1,x2,x3)的矩阵的特征值. (2)设f(x1,x2,x3)的规范形为. 求a


    答案：
    解析：

  • 第17题：

    已知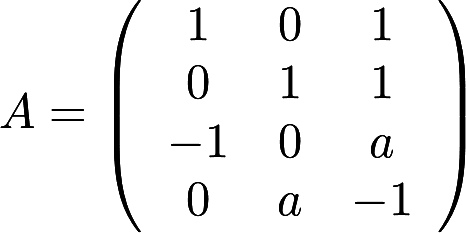，二次型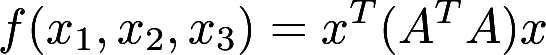的秩为2. （Ⅰ）求实数a的值； （Ⅱ）求正交变换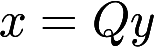将二次型化为标准型


    答案：
    解析：

  • 第18题：

    已知二次型f(x1，x2，3x)=x^TAx在正交变换x=Qy下的标准形为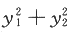，且Q的第3列为.
    　　(Ⅰ)求矩阵A；
    　　(Ⅱ)证明A+E为正定矩阵，其中E为三阶单位矩阵.


    答案：
    解析：

  • 第19题：

    设二次型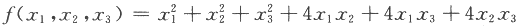，则f(x1，x2，x3)=2在空间直角坐标下表示的二次曲面为

    A.A单叶双曲面
    B.双叶双曲面
    C.椭球面
    D.柱面

    答案：B
    解析：

  • 第20题：

    三阶矩阵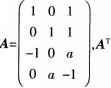 为矩阵A的转置，已知r(ATA)=2，且二次型
    (1)求a；
    (2)求二次型对应的二次矩阵，并将二次型化为标准型，写出正交变换过程。


    答案：
    解析：
    (1)由r(ATA)=r(A)=2可得， (2）

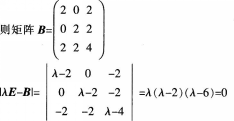
  • 第21题：

    二次型f(x1,x2,x3)=(λ-1)x12+λx22+(λ+1)x32,当满足（ ）时，是正定二次型。
    A. λ>-1 B. λ>0 C. λ>1 D. λ≥1


    答案：C
    解析：
    提示：二次型f(x1,x2,x3)正定的充分必要条件是它的标准形的系数全为正，故 λ-1>0且λ>0且λ+1>0，所以λ>1,应选C。

  • 第22题：

    设事故树的最小径集为{X1，X4}、{X1，X2，X5，X6}、{X2，X3，X4}，求事故树的最小割集。


    正确答案: T=（X1+X4）（X1+X2+X5+X6）（X2+X3+X4）=X1X2+X1X3+X1X4+X2X4+X4X5+X4X6
    最小径集：{X1，X2}，{X1，X3}，{X1，X4}，{X2，X4}，{X4，X5}，{X4，X6}

  • 第23题：

    问答题
    设事故树的最小径集为{X1，X4}、{X1，X2，X5，X6}、{X2，X3，X4}，求事故树的最小割集。

    正确答案： T=（X1+X4）（X1+X2+X5+X6）（X2+X3+X4）=X1X2+X1X3+X1X4+X2X4+X4X5+X4X6
    最小径集：{X1，X2}，{X1，X3}，{X1，X4}，{X2，X4}，{X4，X5}，{X4，X6}
    解析： 暂无解析

相关内容