某次知识竞赛的决赛有3人参加，规则为12道题每题由1人以抢答方式答题，正确得10分，错误扣8分，如果最后所有人得分都是正分，且回答问题最多的人是得分最少的人，那么前两名之间的分差最多为多少分？A．8 B．12 C．20 D．40

第1题：

第2题：

答案：A

解析：

第一步，此题为比赛问题，本题一共10道题，考虑使用枚举法解题。第二步，得分最高为10题都答对，共计30分；得分最低为10题都答错，共计（-10）分，得分都是整数，所以从（-10）到30分，共计有41种得分情况。设做对的题目有a道，做错的题目有b道，没做的题目有c道，则总得分为（3a－b）。



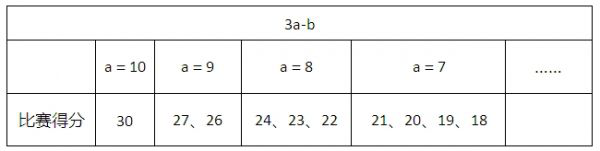
可以发现当a值下降到8后，所得分数从24开始逐渐下降且每个分值都可以得到，所以由表格知道，在-10到30分之间，共有29、28、25三个分数得不到，所以共计有41－3＝38种。因此，选择A选项

第3题：

第4题：

第5题：

第6题：

某班举行数学测验，试题全部是选择题，共10题，每题1分，得分的部分统计结果如下：

已知，得分至少为3分的，人均2x分;得分最多为7分的，人均x分。这个班级总人数是：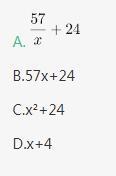

答案：A

解析：

第一步，本题考查平均数问题，用方程法解题。
第二步，设得分至少为3分的人数为y，则全班总分数=2x×y+2×5+1×3=2xy+13①；得分至少为7分的人数为y+5+3+8－2－2－4=y+8，则全班总分数=（y+8）×x+2×10+2×9+4×8=xy+8x+70②。根据①＝②，化简可得xy=8x+57，则

因此，选择A选项。

第7题：

第8题：

答案：C

解析：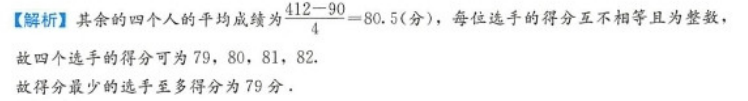

第9题：

某次知识竞赛试卷包括3道每题10分的甲类题，2道每题20分的乙类题以及1道30分的丙类题。参赛者赵某随机选择其中的部分试题作答并全部答对，其最终得分为70分。问赵某未选择丙类题的概率为多少？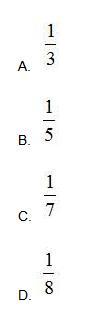

答案：D

解析：

最终得分为70分，则做对的情况为【一】丙类题1，乙类题2：共有1种；【二】丙类题1，乙类题1，甲类题2：共有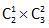

=6种；【三】乙类题2，甲类题3：1种；共计8种。其中不包含丙类题的有1种，概率为1/8。正确答案为D。

第10题：

第11题：

某次知识竞赛试卷包括3道每题10分的甲类题，2道每题20分的乙类题以及1道30分的丙类题。参赛者赵某随机选择其中的部分试题作答并全部答对，其最终得分为70分。问赵某未选择丙类题的概率为多少？（）

• A、1/3
• B、1/5
• C、1/7
• D、1/8

第12题：

第13题：

第14题：

第15题：

第16题：

第17题：

第18题：

答案：C

解析：

第19题：

第20题：

答案：A

解析：

本题属于基础应用题。
黄队比红队少答对2道题，但红、黄两队总分一致，说明红队比黄队：①多错了2道；②多不答4道；③多答错1道同时多不答2道。要求红答题总量最少，则红队先假设只错2道题，如下表：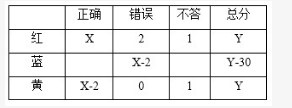

由于每队得分均不少于20分，红队和黄队比蓝队多30分，因此蓝队至少20分，红队=黄队，且至少50分?由于每队至少有一道抢到未答，为了让红队答题数最少，假设红队黄队得分均为55分，如下表：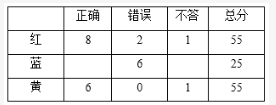

红队答对的为8道，至少抢到了11道题。

第21题：

答案：A

解析：

黄队比红队少正确2道题，但红黄总分一致，说明红队比黄队多错了2道或多不答4道或多答错1道同时多不答2道，要求红答题总量最少，则红队先假设只错2道题，如下表：



由于每队得分均不少于20分，红队和黄队比蓝队多30分，因此蓝队至少20分，红队=蓝队至少50分。由于每队至少有一道抢到未答，为了让红队答题数最少，假设红队黄队得分均为55分，如下表：
红队答对的为8道。

第22题：

某社区组织开展知识竞赛，有5个家庭成功晋级决赛的抢答环节，抢答环节共5道题。计分方式如下：每个家庭有10分为基础分；若抢答到题目，答对一题得5分，答错一题扣2分；抢答不到题目不得分。那么，一个家庭在抢答环节有可能获得（）种不同的分数。

• A、18
• B、21
• C、25
• D、36

第23题：

第24题：