如果把一个体积为125立方厘米的正方体铁块切割成体积相等的8个小正方体，则每 个小正方体铁块的表面积是（）。 A.6.25平方厘米 B.5.625平方厘米 C.16.5平方厘米 D.37.5平方厘米

题目
如果把一个体积为125立方厘米的正方体铁块切割成体积相等的8个小正方体，则每 个小正方体铁块的表面积是（）。

A.6.25平方厘米
B.5.625平方厘米
C.16.5平方厘米
D.37.5平方厘米
相似考题

1.用棱长1cm的小正方体摆成稍大一些的正方体，至少需要多少个小正方体？动手摆摆看。

2.把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体？表面积增加了多少？

3.把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥铁块的高约是多少？（得数保留整厘米。）

4.用体积是1cm³的小正方体木块，堆成一个体积是1m³的大正方体，需要多少个小正方体木块？如果把这些小正方体木块一个挨一个的排成一行，长多少千米？

更多“如果把一个体积为125立方厘米的正方体铁块切割成体积相等的8个小正方体，则每 个小正方体铁块的表面积是（）。 ”相关问题

  • 第1题：

    将27个边长为1的小正方体垒成一个大正方体，然后把大正方体全部涂成红色，请问：三面都被涂成红色的小正方体有多少个？（）。

    A.4

    B.6

    C.8

    D.12


    正确答案：C
    只有正方体8个顶点处的小正方体三面都被涂成红色。故选C。

  • 第2题：

    把一个64cm×40cm×24cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（ ）。

    A．73280cm2

    B．54680cm2

    C．69450cm2

    D．46080cm2


    正确答案：D
    要使这些小正方体的表面积总和最小，那么小正方体的边长要尽可能大。64、40、24的最大公约数为B，因此小正方体的边长为8cm，共有64×40×24÷83=120块。表面积总和为6×82×120=46080cm2。

  • 第3题：

    一个体积为l立方米的立方体，把它切成1立方厘米的小正方体，然后把这些小正方体排成一列，组成一个长方体。这个长方体长多少厘米?（ ）

    A．10

    B．1000000

    C．200

    D．1000


    正确答案：B

    1立方米的正方体可以切割成1000000个1立方厘米的正方体，此时切割成的小正方体的边长为1厘米，则1000000个小正方体排成的长方体的长为1000000厘米。

  • 第4题：

    把一个64Cmx40Cmx24Cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（ ）。

    A．73280cm2

    B．54680cm2

    C．69450cm2

    D．46080cm2


    正确答案：D
    要使这些小正方体的表面积总和最小，那么小正方体的边长要尽可能大。64、40、24的最大公约数为8，因此小正方体的边长为8cm，共有64×40×24÷83＝120块。表面积总和为6×82×120＝46080cm2。

  • 第5题：

    一块各面均涂有油漆的正方体被锯成1000个同样大小的小正方体，将这些小正方体均匀地搅混在一起，随机地取出一个小正方体，其两面涂有油漆的概率是：

    A.0.12
    B.0.096
    C.0.072
    D.0.064

    答案：B
    解析：
    1000＝10×10×10，即每个边上有10块，两面涂有油漆的只能在边上，共有（10－2）×12＝96块，概率为96÷1000＝0.096。

  • 第6题：

    某加工厂要将一个表面积为384平方厘米的正方体金属原材料切割成体积为8立方厘米的小正方体半成品，如果不计损失，这样的小正方体可以加工的个数为

    A. 64
    B. 36
    C. 27
    D. 16

    答案：A
    解析：

  • 第7题：

    用n个棱长是a cm的小正方体可以摆出“一”字形长方体，如图，n个小正方体拼在一起 时，这个长方体表面积是_______cm2。


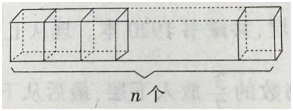    答案：
    解析：
    (4n+2)a2。解析:n个小正方体如题干图中所示拼在一起时，组成长为na，宽为a，高为a的长方体，所以表面积为(4n+2)a2 cm2。

  • 第8题：

    一个长方体木块恰能切割成五个正方体木块，五个正方体木块表面积之和比原来的长方体木块的表面积增加了200cm2。则长方体木块的体积为多少?

    A.625cm3
    B.125cm3
    C.500cm3
    D.750cm3

    答案：A
    解析：
    第一步，本题考查几何问题，属于立体几何类。
    第二步，如图所示，长方体分为5个小正方体，增加了4×2=8（个）阴影部分小正方形的面积，则每个小正方形面积为200÷8=25（cm2），边长为5cm。那么大长方体的体积为5×25×5=625（cm3）。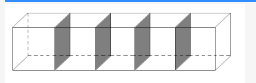

    因此，选择A选项。

  • 第9题：

    将一个表面漆有红色的长方体分割成若干个体积为1立方厘米的小正方体,其中,一点红色也没有的小正方体有4块,那么原来的长方体的体积为（ ）立方厘米

    A.180
    B.54
    C.54或48
    D.64
    E.180或64

    答案：C
    解析：
    没有红色的小正方体位于原来的长方体的内部,这4个小正方体可能排成一字形或田字形；若为一字形:棱长分别为1,1,4,故原长方体的长宽高为3,3,6,体积为3×3×6=54；若为田字形:棱长分别为2,2,1,故原长方体的长宽高为4,4,3,体积为4×4×3=48

  • 第10题：

    体积相等的球和正方体，它们的表面积的大小关系是（）。

    • A、S球＞S正方体
    • B、S球=S正方体
    • C、S球＜S正方体
    • D、不能确定

    正确答案:C

  • 第11题：

    如果把一个体积为125立厘米的正方体铁块切割成体积相等的8个小正方体，则每个小正方体铁块的表面积是( )。

    A．6.25平方厘米

    B．15.625平方厘米

    C．16.5平方厘米

    D．37.5平方厘米

  • 第12题：

    一个正方体木块的体积为1000厘米³，现要把它锯成八块，同样大小的正方体小木块，小木块的棱长是多少？


    锯成8块之后，每小块的正方体体积为1000/8=125厘米³

     

    设小木块的棱长是x，则

    x³=125，x=5厘米

     

  • 第13题：

    如果把一个体积为125立方厘米的正方体铁块切割成体积相等的8个小正方体，则每个小正方体铁块的表面积是：

    A.6.25平方厘米

    B.15.625平方厘米

    C.16.5平方厘米

    D.37.5平方厘米


    正确答案：D

  • 第14题：

    一个体积为8立方米的正方体，如果将它分为体积为8立方分米的正方体，并沿一条直线将它们一个一个连起来，可连（ ）米。

    A．200

    B．100

    C．2000

    D．10000


    正确答案：A
    8立方米=8000立方分米，则8立方米的正方体可以分为1000个8立方分米的正方体，每个小正方体的棱长为2分米，则排成一行之后，总长度为2000分米，即200米。故选A。

  • 第15题：

    在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：

    A.1/4
    B.1/6
    C.1/8
    D.1/10

    答案：C
    解析：
    由题意知切下的角是底面为正三角形、侧面为三个等腰直角三角形的三棱锥，设切下角的直角边为ｘ，则六面体体积＝2×三棱锥体积＝2×(1/3)×(ｘ2/2)×ｘ＝1/24，解得ｘ＝1/2。所以六面体每个面是直角边为1/2的等腰直角三角形，六面体的每个面相当于边长为1的正方形面积的1，所以六面体的表面积为原正方体的1/8。故本题选C。

  • 第16题：

    一个正方体的高增加10cm，得到新长方体的表面积比原正方体表面积增加120cm，原正方体体积是（　　）．

    A.9cm3
    B.12cm3
    C.18cm3
    D.27cm3

    答案：D
    解析：
    如下图所示，高增加10cm后，增加的表面积为四个侧面积.设原正方体的棱长为acm，则有4×10a=120，解得a=3，则原正方体的体积为33=27cm3.

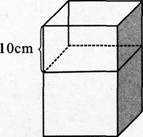
  • 第17题：

    1000个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体，大正方体表面涂油漆后，再分开为原来的小正方体，这些小正方体至少有一面被油漆涂过的数目是多少个：
    A 490
    B 488
    C 484
    D 480


    答案：B
    解析：

  • 第18题：

    一千个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体，大正方体表面涂油漆后再分开为原来的小正方体，这些小正方体至少有一面被油漆涂过的数目是( )个。

    A.490
    B.488
    C.484
    D.480

    答案：B
    解析：
    分析：没有涂色的小正方体都在大正方体的内部，由此先借助正方体的体积公式求出没有涂色的小正方体的个数即可解答．

    解答：解：没有涂色的小正方体：

    （10-2）×（10-2）×（10-2）=8×8×8=512（个），

    所以至少一面涂色的小正方体：1000-512=488（个）

  • 第19题：

    把若干个体积相等的正方体拼成一个大正方体,在表面涂上红色,已知一面涂色的小正方体有96个,则两面涂色的小正方体有（ ）个

    A.48
    B.60
    C.64
    D.24
    E.32

    答案：A
    解析：
    一面涂色的小正方体位于大正方体的面上（除去機上的）,每个面有4×4=16（个）,令小正方体的边长为1,则大正方体的边长为6;两面涂色的小正方体位于大正方体的機上（除去8个角）,每条棱上有4个,故总个数为4×12=48

  • 第20题：

    单选题
    在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：
    A

    1/4

    B

    1/6

    C

    1/8

    D

    1/10


    正确答案： A
    解析：

相关内容