依据Johnson算法得出的最优顺序,若从中去掉某些工件得出的顺序仍为余下工件的最优顺序。()此题为判断题(对，错)。

题目
依据Johnson算法得出的最优顺序,若从中去掉某些工件得出的顺序仍为余下工件的最优顺序。()

此题为判断题(对，错)。

相似考题

1.按Johnson算法得出的最优顺序,若从中去掉某些工件得出的顺序仍为余下工件的最优顺序。()此题为判断题(对，错)。

2.在铣床上对多个工件的加工方法有()。A、顺序B、平行C、平行顺序

3.已知矩阵 Am*n和 Bn*p 相乘的时间复杂度为 O（mnp）矩阵相乘满足结合律,如三个矩阵A、B、C 相乘的顺序可以是（A*B）*C）,也可以是A*（B*C）.不同的相乘序所需进行的乘法次数可能有很大的差别,因此确定n 个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n 个短阵 A,A2........An 相乘的计算顺序具有最优子结构,即 A1A2..........An 的最优计算顺序包含其子问题A1A2.......Ak和 Ak+1Ak+2.......An（可以列出其递归式为其中,A 的维度为 pi-1*pim【i,j】,表示 AiAi+1…A j最优计算顺字的相乘次数, 先釆用自底向上的方法求n 个矩阵相乘的最优计算顺序。则该问题的算法设计策略为（ ）,算法的时间复杂度为（ ）,空间复杂度为（请作答此空） 给定一个实例,（POPi........P5）=（20.15.4.10.20.25）最优计算顺序为（ ）A.O（n^2） B.O（n*2lgn） C.O（n^3） D.O（2n）

4.按照Johnson法则如得到多个加工顺序，则应从中取最优者。()

参考答案和解析
正确答案：正确
更多“依据Johnson算法得出的最优顺序,若从中去掉某些工件得出的顺序仍为余下工件的最优顺序。() ”相关问题

  • 第1题：

    已知阳阵 Am*n和 Bn*p 相乘的时间复杂度为 O（mnp）矩阵相乘满足结合律,如三个矩阵A、B、C 相乘的顺序可以是（A*B）*C）,也可以是A*（B*C）.不同的相乘序所需进行的乘法次数可能有很大的差别,因此确定n 个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n 个短阵 A,A2........An 相乘的计算顺序具有最优子结构,即 A1A2..........An 的最优计算顺序包含其子问题A1A2.......Ak和 Ak+1Ak+2.......An（<=kcn）的最优计算顺序。
    可以列出其递归式为



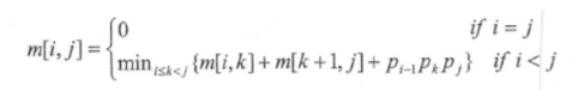
    其中,A 的维度为 pi-1*pi，m【i,j】,表示 AiAi+1…A j最优计算顺字的相乘次数,
    先釆用自底向上的方法求n 个矩阵相乘的最优计算顺序。则该问题的算法设计策略为（请作答此空）,算法的时间复杂度为（ ）,空间复杂度为（ ）
    给定一个实例,（P0Pi........P5）=（20.15.4.10.20.25）最优计算顺序为（ ）

    A.分治法
    B.动态规划法
    C.贪心法
    D.回溯法

    答案：B
    解析：
    题干提到该问题具有最优子结构，并且由m[i,j]表示 AiAi+1…A j最优计算顺字的相乘次数，因此可判断该算法为动态规划法。

  • 第2题：

    16、对于动态规划的描述，下面说法不正确的是（）

    A.动态规划的核心是基本方程#B.对于同一个动态规划问题，应用顺序和逆序两种解法会得到相同的最优解#C.若动态规划问题的初始状态是已知的，一般采用顺序解法进行求解#D.最优性原理可以描述为策略具有的基本性质是无论初始状态和初始决策如何，对于前面决策所造成的某一状态而言，余下的决策序列必构成最优策略
    最优化原理可以描述为 “ 策略具有的基本性质是：无论初始状态和初始决策如何，对于前面决策所造成的某一状态而言，余下的决策序列必构成最优策略 ”

  • 第3题：

    已知有6个工件需要在两台设备上加工的流水作业，单件加工时间矩阵如下表所示。应用Johnson算法确定最优加工排序和相应的最长流程时间。 加工时间矩阵 单位：分钟 工件序号 工件1 工件2 工件3 工件4 工件5 工件6 设备1 设备2 8分钟 3分钟 4分钟 2分钟 7分钟 6分钟 1分钟 9分钟 3分钟 2分钟 10分钟 5分钟


    C

  • 第4题：

    已知矩阵 Am*n和 Bn*p 相乘的时间复杂度为 O（mnp）矩阵相乘满足结合律,如三个矩阵A、B、C 相乘的顺序可以是（A*B）*C）,也可以是A*（B*C）.不同的相乘序所需进行的乘法次数可能有很大的差别,因此确定n 个矩阵相乘的最优计算顺序是一个非常重要的问题。已知确定n 个短阵 A,A2........An 相乘的计算顺序具有最优子结构,即 A1A2..........An 的最优计算顺序包含其子问题A1A2.......Ak和 Ak+1Ak+2.......An（<=kcn）的最优计算顺序。
    可以列出其递归式为



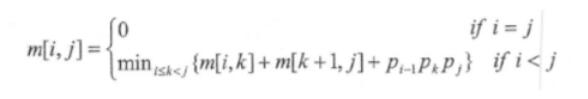
    其中,A 的维度为 pi-1*pim【i,j】,表示 AiAi+1…A j最优计算顺字的相乘次数,
    先釆用自底向上的方法求n 个矩阵相乘的最优计算顺序。则该问题的算法设计策略为（ ）,算法的时间复杂度为（请作答此空）,空间复杂度为（ ）
    给定一个实例,（POPi........P5）=（20.15.4.10.20.25）最优计算顺序为（ ）

    A.O（n^2）
    B.O（n^2lgn）
    C.O（n^3）
    D.O（2^n）

    答案：C
    解析：
    矩阵链乘法： 一个给定的矩阵序列A1A2...An计算连乘乘积，有不同的结合方法，并且在结合时，矩阵的相对位置不能改变，只能相邻结合。根据矩阵乘法的公式，10*100和100*5的矩阵相乘需要做10*100*5次标量乘法。那么对于维数分别为10*100、100*5、5*50的矩阵A、B、C，用(A*B)*C来计算需要10*100*5 + 10*5*50 =7500次标量乘法；而A*(B*C)则需要100*5*50+10*100*50=75000次标量乘法。根据题干有A1-A5五个矩阵，分别为：20*15、15*4、4*10、10*20、20*25，分别带入65题各个选项，得到选项D是计算次数最少的选项。具体计算结果为：选项A：A1*A2=20*15*4=1200，(A1*A2)*A3)=20*4*10=800，(((A1*A2)*A3)*A4)=20*10*20=4000，(((A1*A2)*A3)*A4)*A5=20*20*25=10000，总的计算次数为1200+800+4000+10000=16000次。选项B：A4*A5=10*20*25=5000，A3*(A4*A5)=4*10*25=1000，A2*(A3*(A4*A5))=15*4*25=1500，A1*(A2*(A3*(A4*A5)))=20*15*25=7500，总的计算次数为：5000+1000+1500+7500=15000次。选项C：A1*A2=20*15*4=1200，(A1*A2)*A3)=20*4*10=800，A4*A5=10*20*25=5000，((A1*A2)*A3)*(A4*A5)=20*10*25=5000，总的计算次数为1200+800+5000+5000=12000次。选项D：A1*A2=20*15*4=1200，A3*A4=4*10*20=800，(A3*A4)*A5=4*20*25=2000，(A1*A2）*((A3*A4)*A5)=20*4*25=2000，总的计算次数为1200+800+2000+2000=6000次。该算法的，pi 1pkpj的值需要三重循环解决，因此时间复杂度为O（n^3），空间复杂度为O（n^2）。

  • 第5题：

    某工程项目需要做五个核心的工件1、工件2、工件3、工件4、工件5，它们都是需要在2台设备上加工，加工顺序相同，都是先在设备1上加工，再在设备2上加工，各个工件在各台设备上加工的工时见下表,表中字母表示活动代码，数字表示活动时间，已知五个工件同时到达项目工地，为了使项目时间节省，试求五个工件最优排序方案并计算其总工时，并绘制该最优排序方案的项目网络图。单位：小时 工件 工件1 工件2 工件3 工件4 工件5 设备1 A 12 B 6 C 4 D 2 E 3 设备2 M 5 N 9 P 11 Q 1 W 7


    A

相关内容