设矩阵A,B,C,X为同阶方阵,且A,B可逆,AXB=C,则矩阵X=()A、A^-1CB^-1B、CA^-1B^-1C、B^-1A^-1CD、CB^-1A^-1
题目
设矩阵A,B,C,X为同阶方阵,且A,B可逆,AXB=C,则矩阵X=()
A、A^-1CB^-1
B、CA^-1B^-1
C、B^-1A^-1C
D、CB^-1A^-1
相似考题
更多“设矩阵A,B,C,X为同阶方阵,且A,B可逆,AXB=C,则矩阵X=() ”相关问题
-
第1题:
设A为3阶矩阵.P为3阶可逆矩阵,且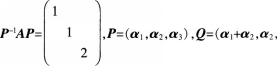
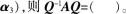
A.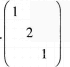
B.
C.
D.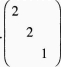 答案:B解析:
答案:B解析: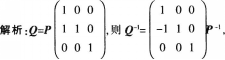
 故选B。
故选B。 -
第2题:
若矩阵A和矩阵B为同阶方阵,则AB=BA。()
错误 -
第3题:
设A为5阶方阵,A*是其伴随矩阵,且|A|=3,则|A*|=_______
-2 -
第4题:
设A、B为同阶可逆矩阵,则《》( ) 答案:D解析:
答案:D解析: -
第5题:
3、若矩阵A和矩阵B为同阶方阵,则AB=BA。()
错误
