线性方程组Ax=0，若是A是n阶方阵，且R（A）A.有唯一解 B.有无穷多解 C.无解 D. A，B，C皆不对
题目
线性方程组Ax=0，若是A是n阶方阵，且R（A）
A.有唯一解
B.有无穷多解
C.无解
D. A，B，C皆不对
B.有无穷多解
C.无解
D. A，B，C皆不对
相似考题
参考答案和解析
答案：B
解析：
提示：当方阵的行列式 A ≠0，即R（A）=n时，Ax = 0仅有唯一解，当 A =0， 即R（A）
更多“线性方程组Ax=0，若是A是n阶方阵，且R（A）”相关问题
-
第1题：
若A是m×n矩阵，且m≠n，则当R（A）=m时，非齐次线性方程组AX=b，有解答案：对解析： -
第2题：
设n元齐次线性方程组Ax=0的系数矩阵A的秩为r，则Ax=0有非零解的充要条件为（ ）。A.r=n
B.r＜n
C.r≥n
D.r＞n答案：B解析：Ax=0有非零解的充要条件为｜A｜=0，即矩阵A不是满秩的，r＜n。 -
第3题：
设A为n阶矩阵,且｜A｜=0,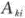
≠0,则AX=0的通解为_______.答案：解析：
-
第4题：
设A是m×n阶矩阵,且非齐次线性方程组AX=b满足r(A)=r(A)=r答案：解析：
第5题：
设A为n阶方阵，且 A =a≠0，则 An 等于（ ）。
A. a B. 1/a C.an-1 D. an答案：C解析：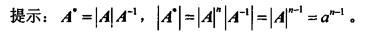
第6题：
填空题设A、B都是4阶方阵且AB＝0，则r（A）＋r（B）____。正确答案： ≤4解析：
由AB＝0，知矩阵B的列向量是方程组AX＝0的解，令r（A）＝r1，r（B）≤4－r1，故r（A）＋r（B）≤4。第7题：
填空题设A、B、C均为n阶方阵，若A＝CTBC，且|B|＜0，则|A|____。正确答案： ≤0解析：
由行列式性质可知|A|＝|CT|·|B|·|C|＝|C|2·|B|≤0。第8题：
问答题设AX=0与BX=0均为n元齐次线性方程组，秩r（A）=r（B），且方程组AX=0的解均为方程组BX=0的解，证明方程组AX=0与BX=0同解.正确答案：
设r(A)=r(B)=r,方程组AX=0的基础解系为①:ζ1,ζ2,…,ζn-r,方程组BX=0的基础解系为②:η1,η2,…,ηn-r.
构造向量组③:ζ1,ζ2,…,ζn-r,η1,η2,…,ηn-r.
由向量组①可由②线性表示,则向量组②和③等价,从而r(③)=n-r,所以ζ1,ζ2,…,ζn-r是向量组③的极大线性无关组,有η1,η2,…,ηn-r可由ζ1,ζ2,…,ζn-r线性表示,即BX=0的任一解都可由ζ1,ζ2,…,ζn-r线性表示,故BX=0的解都是AX=0的解,所以方程组AX=0与BX=0同解.解析： 暂无解析第9题：
单选题设A为n阶方阵，则n元齐次线性方程组AX(→)＝0(→)仅有零解的充要条件是|A|（ ）。A＝0
B≠0
C＝1
D≠1
正确答案： B解析：
依据齐次线性方程组性质可知，系数行列式|A|≠0时，方程组仅有零解。第10题：
单选题设A为3阶方阵，α(→)1，α(→)2，α(→)3是互不相同的3维列向量，且都不是方程组Ax(→)＝0(→)的解，若B＝（α(→)1，α(→)2，α(→)3）满足r（AB）＜r（A），r（AB）＜r（B），则r（AB）等于（ ）。A3
B2
C1
D0
正确答案： C解析：
由于α1，α2，α3不是Ax＝0的解，故AB≠0，所以r（AB）＞0。
又因r（AB）＜r（A），故B不可逆，即r（B）≤2，从而r（AB）＜r（B）≤2，即r（AB）＝1。第11题：
问答题设A为n阶方阵，若对任意n维向量x(→)＝（x1，x2，…，xn）T都有Ax(→)＝0。证明：A＝0。正确答案：
由对任意n维向量x都有Ax=0,知对基本单位向量组ε1,ε2,…,εn,Aεi=0(i=1,2,…,n)成立。
所以有A(ε1,ε2,…,εn)=0,即AE=0,故A=0。解析： 暂无解析第12题：
填空题设n阶矩阵A的各行元素之和均为零，且A的秩为n－1，则线性方程组AX(→)＝0(→)的通解为____。正确答案： X=k(1,1,…,1)T解析：
由r（A）＝n－1，知方程组AX＝0的基础解系只含有n－（n－1）＝1个解向量。又矩阵A的各行元素之和为0，知（1，1，…，1）T，为AX＝0的非零解，则方程组AX＝0的通解为X＝k（1，1，…，1）T。第13题：
若A是m×n矩阵，且m≠n，则当R（A）=n时，非齐次线性方程组AX=b，有唯一解答案：错解析：第14题：
已知3阶矩阵A的第一行是
不全为零，矩阵 
（k为常数），且AB=0, 求线性方程组Ax=0的通解答案：解析：
第15题：
设A为n阶矩阵,A的各行元素之和为0且r(A)=n-1,则方程组AX=0的通解为_______.答案：解析：
第16题：
设A，B是n阶方阵，A≠0且AB=0，则（ ）.
A.|
B.B=0；
C.BA=O：
D.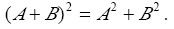
答案：A解析：第17题：
设A为n阶方阵，且|A|=a≠0，则|A*|等于（）。
- A、a
- B、an-1
- C、an
正确答案:C第18题：
填空题设n阶矩阵A的各行元素之和均为零，且A的秩为n-1，则线性方程组AX=O的通解为____.正确答案： X=k(1,1…,1)T解析：
由r（A）＝n-1，知方程组AX=0的基础解系只含有n-（n-1）=1个解向量．又矩阵A的各行元素之和为0，知（1，1，…，1）T，为AX=0的非零解，则方程组AX=0的通解为X＝k（1，1…，1）T．第19题：
单选题线性方程组Ax=0，若是A是n阶方阵，且R（A）（）A有唯一解
B有无穷多解
C无解
DA，B，C皆不对
正确答案： A解析： 暂无解析第20题：
填空题设A为n阶方阵，则n元齐次线性方程组AX(→)＝0(→)仅有零解的充要条件是|A|____。正确答案： ≠0解析：
依据齐次线性方程组性质可知，系数行列式|A|≠0时，方程组仅有零解。第21题：
单选题设A为n阶方阵，则n元齐次线性方程组AX(→)＝0(→)仅有零解的充要条件是|A|（ ）。A＜0
B≠0
C＞0
D＝0
正确答案： A解析：
依据齐次线性方程组性质可知，系数行列式|A|≠0时，方程组仅有零解。第22题：
单选题n元线性方程组AX(→)＝b(→)有唯一解的充要条件为（ ）。AA为方阵且｜A｜≠0
B导出组AX＝0仅有零解
C秩（A）＝n
D系数矩阵A的列向量组线性无关，且常数向量b与A的列向量组线性相关
正确答案： C解析：
A项，系数矩阵A不一定是方阵；B项，导出组只有零解，方程组AX＝b不一定有解；C项，当r（A）＝n时，不一定有r（A）＝r（A）＝n；D项，b可由A的列向量组线性表示，则方程组AX＝b有唯一解。第23题：
问答题设A为n阶方阵，若对任意n维向量X=（x1，x2，…，xn）T都有AX=0.证明：A=0.正确答案：
证明:由对任意n维向量X都有AX=0,知对基本单位向量组ε1,ε2,…,εn,Aεi=0(i=1,2,…,n)成立.
所以有A(ε1,ε2,…,εn)=0,即AE=0,故A=0.解析： 暂无解析