设A是n阶方阵，a是n维列向量，下列运算无意义的是( ).A. B. C.αA D.Aα
题目
设A是n阶方阵，a是n维列向量，下列运算无意义的是( ).
A.
B.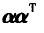
C.αA
D.Aα
B.
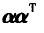
C.αA
D.Aα
相似考题
更多“设A是n阶方阵，a是n维列向量，下列运算无意义的是( ).”相关问题
-
第1题：
设A，B都是n阶方阵，下列等式不正确的是( ).A.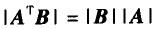
B.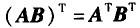
C.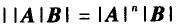
D.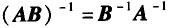
答案：B解析：
-
第2题：
设A，B是n阶方阵，下列等式成立的是( ).A.
B.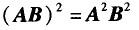
C.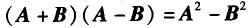
D.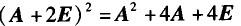
答案：D解析：
-
第3题：
设A、B均为n阶方阵，则下列式子中错误的是（ ）.
答案：D解析：
-
第4题：
设Amxn,Bnxm(m≠n)，则下列运算结果不为n阶方阵的是：
A.BA B.AB C. (BA)T D.ATBT答案：B解析：提示:选项A，Amxn,Bnxm=(BA)nxn，故BA为n阶方阵。
选项B，Amxn,Bnxm= (AB)mxm，故AB为m阶方阵。
选项C，因BA为n阶方阵，故其转置(BA)T也为n阶方阵。
选项D，因ATBT= (BA)T，故ATBT也是n阶方阵。 -
第5题：
设A是nxm矩阵，B是mxn矩阵，E是n阶单位阵，若AB=E，证明B的列向量组线性无关。答案：解析：
-
第6题：
设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵
.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.
答案：解析：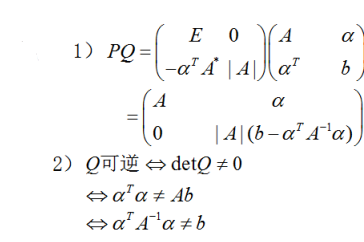
-
第7题：
设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（ ）.
答案：D解析：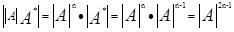
-
第8题：
设A是n阶方阵，α是n维列向量，下列运算无意义的是（）．
- A、αTAα
- B、ααT
- C、αA
- D、Aα
正确答案:C -
第9题：
单选题已知A为奇数阶实矩阵，设阶数为n，且对于任一n维列向量X，均有XTAX＝0，则有（ ）。A｜A｜＞0
B｜A｜＝0
C｜A｜＜0
D以上三种都有可能
正确答案： D解析：
由于对任一n维列向量X均有XTAX＝0，两边转置，有XTATX＝0，从而XT（A＋AT）X＝0。显然有（A＋AT）T＝A＋AT，即A＋AT为对称矩阵。从而对任一n维列向量X均有：XT（A＋AT）X＝0，A＋AT为实对称矩阵，从而有A＋AT＝0。即AT＝－A，从而A为实反对称矩阵，且A为奇数阶，故｜A｜＝0。 -
第10题：
问答题设A＝E－α(→)α(→)T，其中E是n阶单位矩阵，α(→)是n维非零列向量，α(→)T是α(→)的转置。证明： （1）A2＝A的充要条件是α(→)Tα(→)＝1； （2）当α(→)Tα(→)＝1时，A是不可逆矩阵。正确答案：
(1)必要性:由A=E-ααT,可知
A2=(E-ααT)(E-ααT)=E-ααT-ααT +(ααT)(ααT)=E-2ααT+α(αTα)αT=E-ααT +(αTα-1)ααT
若A2=A=E-ααT,则(αTα-1)ααT=0,因为α为非零向量,故ααT≠0,所以有αTα-1=0,即αTα=1。
充分性:若ααT=1,即ααT-1=0,则A2=E-ααT+(αTα-1)ααT=E-ααT=A。
(2)(反证法)
若ααT=1,则有A2=A。如果矩阵A可逆,则有A-1A2=A-1A=E,即A=E,这与A=E-ααT相矛盾(由α是n维非零列向量,故ααT≠0),故矩阵A不可逆。解析： 暂无解析 -
第11题：
问答题设A为n阶方阵，若对任意n维向量X=（x1，x2，…，xn）T都有AX=0.证明：A=0.正确答案：
证明:由对任意n维向量X都有AX=0,知对基本单位向量组ε1,ε2,…,εn,Aεi=0(i=1,2,…,n)成立.
所以有A(ε1,ε2,…,εn)=0,即AE=0,故A=0.解析： 暂无解析 -
第12题：
设A，B是n（n≥2）阶方阵，则必有（ ）.
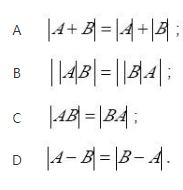答案：C解析： -
第13题：
设Am×n，Bn×m（m≠n），则下列运算结果不为n阶方阵的是:A.BA
B.AB
C.（BA）T
D.ATBT答案：B解析：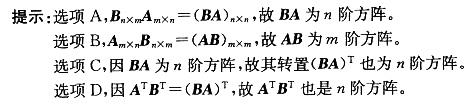
-
第14题：
设A，B均为n 阶方阵，下面结论正确的是( ).
答案：B解析：
-
第15题：
设A为n阶矩阵,证明：r(A)=1的充分必要条件是存在n维非零列向量α,β使得A=αβT.答案：解析：
-
第16题：
设x为n维列向量,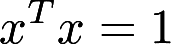
,令,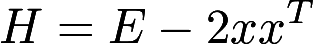
证明H是对称的正交阵.答案：解析：
-
第17题：
设α1,α2,…,αn为n个线性无关的n维列向量,且与向量β正交.证明：向量β为零向量.答案：解析：
-
第18题：
设A是n阶方阵，n≥3．已知|A|=0，则下列命题正确的是（）．
- A、A中某一行元素全为0
- B、A的第n行是前n-1行（作为行向量）的线性组合
- C、A中有两列对应元素成比例
- D、A中某一列是其余n-1列（作为列向量）的线性组合
正确答案:D -
第19题：
单选题设A是n阶方阵，α是n维列向量，下列运算无意义的是（）．AαTAα
BααT
CαA
DAα
正确答案： B解析： （A）有意义，它是1×n阵、n×n阵、n×1阵依次相乘，乘得的结果是1×1阵，即是一个数．（B）有意义，它是n×1阵与1×n阵相乘，乘得的结果是n阶方阵．（D）有意义，它是n×n与n×1阵相乘，乘得的结果是列向量．（C）无意义，因为n×1阵与n×n阵不能相乘，故选（C）. -
第20题：
单选题设A是n阶方阵，n≥3．已知|A|=0，则下列命题正确的是（）．AA中某一行元素全为0
BA的第n行是前n-1行（作为行向量）的线性组合
CA中有两列对应元素成比例
DA中某一列是其余n-1列（作为列向量）的线性组合
正确答案： A解析： 暂无解析 -
第21题：
问答题设A为n阶方阵，若对任意n维向量x(→)＝（x1，x2，…，xn）T都有Ax(→)＝0。证明：A＝0。正确答案：
由对任意n维向量x都有Ax=0,知对基本单位向量组ε1,ε2,…,εn,Aεi=0(i=1,2,…,n)成立。
所以有A(ε1,ε2,…,εn)=0,即AE=0,故A=0。解析： 暂无解析