发报台分别以概率0. 6和0. 4发出信号“ * ”和“一”，由于受到干扰，接受台不能完全准确收到信号，当发报台发出“ * ”时，接受台分別以概率0. 8和0. 2收到“ * ”和“一”；当发报台发出“一”时，接受台分别以概率0. 9和0. 1收到“一”和“ * ”，那么当接受台收到“ *” 时，发报台发出“ *”的概率是： A.13/25 B.12/13 C.12/25 D.24/25
题目
发报台分别以概率0. 6和0. 4发出信号“ * ”和“一”，由于受到干扰，接受台不能完全准确收到信号，当发报台发出“ * ”时，接受台分別以概率0. 8和0. 2收到“ * ”和“一”；当发报台发出“一”时，接受台分别以概率0. 9和0. 1收到“一”和“ * ”，那么当接受台收到“ *” 时，发报台发出“ *”的概率是：
A.13/25
B.12/13
C.12/25
D.24/25
B.12/13
C.12/25
D.24/25
相似考题
参考答案和解析
答案：B
解析：
更多“发报台分别以概率0. 6和0. 4发出信号“ * ”和“一”，由于受到干扰，接受台不能完全准确收到信号，当发报台发出“ * ”时，接受台分別以概率0. 8和0. 2收到“ * ”和“一”；当发报台发出“一”时，接受台分别以概率0. 9和0. 1收到“一”和“ * ”，那么当接受台收到“ *” 时，发报台发出“ *”的概率是： ”相关问题
-
第1题：
一个工人看管3台车床，在1小时内任1台车床不需要人看管的概率为0. 8，3台机床工作相互独立，则1小时内3台车床中至少有1台不需要人看管的概率是：A. 0. 875
B. 0. 925
C. 0. 765
D. 0. 992答案：D解析：提示：设A表示“1小时内3台车床至少有1台不要人看管”，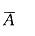
表示“1小时内3台均要人看管”，P(A) = 1-P(
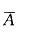)，P(
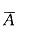)=0.23。或设X为3台车床中不需看管的台数，则X~B (3,0. 8),P(X≥1) =1-P(X=0)。 -
第2题：
确定可以接受的信度水平的一般原则是，当（ ）时，测验因不可靠而不能 使用。
(A) rxx=0. 70 (B) 0. 70≤rxx 0. 85
(C) rxx≥0. 85 (D) rxx = 1. 00答案：A解析： -
第3题：
—台三相交流电机定子绕组，极数2p=6，定子槽数z1 =54槽，线圈节距y1 =9槽，那么此绕组的基波绕组因数Kwl为（）。
A. 0.945
B. 0. 96
C. 0. 94
D. 0. 92答案：B解析：
-
第4题：
两台机床相互独立工作，需要维修的概率分别是0.3与0.2，下列结果中正确的有 ( )。
A.两台机床都不需要维修的概率是0.56
B.至少有一台机床不需要维修的概率是0. 06
C.至多有一台机床需要维修的概率是0. 94
D.两台机床都需要维修的概率是0. 06
E.只有一台机床需要维修的概率是0.14答案：A,D解析：设两台机床需要维修的概率分别为P(A)、P(B)，则P(A)=0.3，P(B)=0.2。
A项，两台机床都不需要维修的概率为：
D项，两台机床都需要维修的概率为：P(AB)=0. 3 x0. 2 =0. 06。
E项，只有一台机床需要维修的概率是：
=0.7x0.2+0.3x0.8=0.38。 -
第5题：
两样本平均数比较作t检验时，分别取以下检验标准，以()所犯第二类错误的概率最小。A.α =0. 01
B.α=0. 05
C.α=0. 001
D.α=0. 10答案：D解析：推断统计；假设检验；假设检验的原理。 犯I类错误的概率为α，这个α是我们自己设的。犯Ⅱ类错误的概率为p。在其他条件不变时，α 越大，β越小。A、B、C、D四个选项里，D是α最大的，所以D的β最小。涉及两类错误的题目，画图有助于理解。 -
第6题：
某系统由A、B两个部分组成，两部分工作相互独立，且两部分均失效才能导致系统失效，若A部分的失效概率为0. 2，B部分的失效概率为0. 1，则系统失效概率为（ ）。
A. 0. 02 B. 0. 08 C. 0. 18 D. 0. 72答案：A解析：已知A、B两部分工作相互独立，故P（系统失效）=P（A部分失效且B部分失效）=P（A部分失效）×P（B部分失效）=0.2×0. 1 =0.02。 -
第7题：
设每台电脑在一年内需要修理的概率为0.02,某单位有50台这种电脑，则在一年内需要修理的电脑不多于两台的概率为（ ）。
A. 0. 186 B. 0. 364 C. 0. 372 D. 0. 922答案：D解析：
-
第8题：
拍发转报时，当收到转报台的收据后，还应向收报台索取收据，在记录该份转报的发出时间时，应以转报台给收据的时间为准。
正确答案:错误 -
第9题：
一个好的抽样检验方案，应该具备（）。
- A、当质量较好时，应该以高概率接受
- B、当质量较好时，以高概率拒收
- C、当质量较差时，以高概率拒收
- D、当质量较差时，以高概率接受
- E、尽量以高概率接受
正确答案:A,C -
第10题：
电源系统中安装了两台EGIU（电源接口组件），它们分别接受哪个系统的信号？（）
- A、两台EGIU分别接受相应GCU1、2的参数信号
- B、两台EGIU分别接收外电源和APU发电机的参数信号
- C、一台EGIU接收外电源和APU发电机的参数信号；另一台接收GCU1、2的参数信号
- D、一台EGIU接收GCU1和外电源的参数信号；另一台EGIU接收GCU2和APU发电机的参数信号
正确答案:D -
第11题：
甲乙两人独立地向同一目标各射击一次，命中率分别为0. 8和0. 6，现已知目标被击中，则它是甲射中的概率为：A. 0. 26
B. 0. 87
C. 0. 52
D. 0. 75答案：B解析：提示：设“甲击中”为A，“乙击中”为B，A、B独立，目标被击中即甲、乙至少一人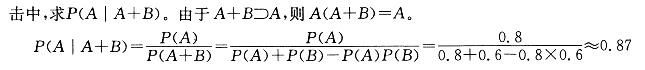
-
第12题：
小王开车上班需经过4个交通路口，假设经过每个路口遇到红灯的概率分别为0. 1，0.2，0.25，Q.4,则他上班经过4个路口至少有一处遇到绿灯的概率是（ ）。A. 0. 899
B. 0.988
C. 0. 989
D. 0. 998答案：D解析：本题属于概率问题。可以采用逆向考虑,至少有一处遇到绿灯的对立面是遇到的全是红灯，所以概率为1 -0.1 x 0.2x0. 25x0. 4 = 0. 998，所以正确答案选择D。 -
第13题：
有一批1000件的产品送检，若采用(20，3)的抽样方案，当p=10%时的接收概率是()。
A. 0. 133 B. 0. 821 C. 0. 867 D. 0. 995答案：C解析：根据题意，N=1000, n=20, Ac=3,则n/N
，代入数据求得：
-
第14题：
甲的投篮命中率为0.8，乙为0.7。二人比赛时约定，乙投一次之后甲再投，若有一人投进而另一人未投进，则投进者胜；若二人都投进或都未投进，则比赛继续。那么乙获胜的概率约为（ ）。A. 0.1—0. 2
B. 0. 3—0. 4
C. 0. 4—0. 5
D. 0. 5—0. 6答案：B解析：假设只进行了一局比赛，此时乙获胜的概率为0.7 X (1－0.8) = 1 X 0.14,甲获胜的概率为0.8X(1－0.7) = 1X0.24；假设进行了两局比赛，此时乙获胜概率为 [0. 7 X 0. 8+ (1 －0. 7) X (1 －0.8) ]X 0. 7 X (1 －0.8) = 0.62 X 0.14，甲获胜的概率为 [0.7X0.8+(1 －0.7) X (1－0.8) ]X 0.8 X (1 －0. 7) = 0.62 X0. 24。由此可见，进行i+1局比赛才决出胜负，面i局比赛都没有决出胜负的概率记为Pi，则乙获胜概率为0.14Pi，甲获胜概率为0. 24Pi。故综合一切可能，乙获胜的概率为
-
第15题：
一自动报警器由雷达和计算机两部分组成，两部分工作相互独立，且任一部分失效将导致报警器失效。若雷达失效概率为0.1，计算机失效概率为0.05，则该报警器失效的概率为（ ）。
A. 0. 005 B. 0. 145 C. 0. 150 D. 0. 205答案：B解析：P（报警器失效）=P（雷达失效且计算机正常）+P（雷达正常且计算机失效）+P （雷达失效且计算机失效）=0. 1 × 0.95 +0.9 ×0.05 +0. 1 ×0.05 =0. 145。 -
第16题：
由4个元件串联组装而成的一台设备，若各元件故障的发生相互独立，每个元件正常工作的概率为0.9，则该设备正常工作的概率为（ ）。
A. 0. 000 1 B. 0. 656 1
C. 0. 818 1 D. 0. 999 9答案：B解析：。设备正常工作的概率为0.94。 -
第17题：
两台机床相互独立工作，需要维修的概率分别是0.3与0.2，两台机床都不需要维修的概率是（）。
A. 0. 56 B. 0. 06
C. 0. 94 D. 0. 14答案：A解析：。设事件A= “甲机床需要维修”，事件B=“乙机床需要维修”，两台机床都不需要维修的概率为 P(AB) = P(A)P(B)=0. 7×0. 8=0. 56。 -
第18题：
通播电台发给网内各属台时，应与（）沟通后再发报。
- A、全部或部分属台
- B、主要属台
- C、约定的属台
- D、第一个属台
正确答案:A -
第19题：
电报发往转报台后，应在附注栏内签名记时，并注明（）代号，但不等于电报的最后发出，还应继续联络收报台，并及时询问转报台转报情况。
- A、发报台
- B、收报台
- C、转报台
- D、发报台和收报台
正确答案:C -
第20题：
问答题27.一大楼装有5台同类型的供水设备，调查表明在任一时刻，每台设备被使用的概率为0.1，问同一时刻， (1)恰有2台设备被使用的概率是多少? (2)至少有3台设备被使用的概率是多少? (3)至多有3台设备被使用的概率是多少? (4)至少有1台设备被使用的概率是多少?正确答案：解析：