化二重积分为极坐标系下的二次积分,则等于下列哪一式?
题目
化二重积分为极坐标系下的二次积分,则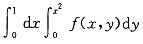 等于下列哪一式?
等于下列哪一式?
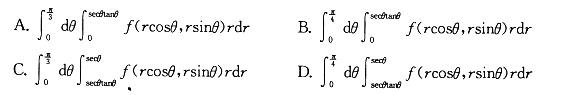
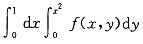 等于下列哪一式?
等于下列哪一式?
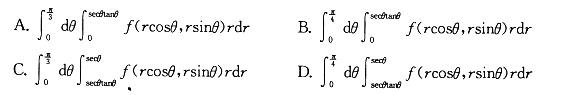
相似考题
更多“化二重积分为极坐标系下的二次积分,则等于下列哪一式? ”相关问题
-
第1题:
 在极坐标系下的二次积分是:
在极坐标系下的二次积分是:
 答案:B解析:
答案:B解析:

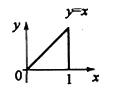
-
第2题:
设二重积分 交换积分次序后,则I等于下列哪式?
交换积分次序后,则I等于下列哪式?
 答案:A解析:提示:画出积分区域D的图形,再写出先x后y的积分表达式。如下:
答案:A解析:提示:画出积分区域D的图形,再写出先x后y的积分表达式。如下:

-
第3题:
下列定积分中,哪一个等于零? . 答案:C解析:提示:逐一计算每一小题验证,首先考虑利用奇函数在对称区间积分为零这一性质。
答案:C解析:提示:逐一计算每一小题验证,首先考虑利用奇函数在对称区间积分为零这一性质。 -
第4题:
 (其中D:x2+y2≤1)化为极坐标系下的二次积分,其形式为下列哪一式?
(其中D:x2+y2≤1)化为极坐标系下的二次积分,其形式为下列哪一式?
 答案:D解析:提示:化为极坐标系下的二次积分,面积元素dσ=rdrdθ,把x=rcosθ,y=rsinθ代入。
答案:D解析:提示:化为极坐标系下的二次积分,面积元素dσ=rdrdθ,把x=rcosθ,y=rsinθ代入。 -
第5题:
已知平面区域 ,计算二重积分
,计算二重积分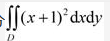 答案:解析:
答案:解析:
-
第6题:
计算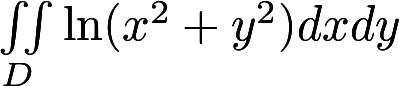 , D:
, D: 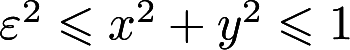 , 并求上述二重积分当
, 并求上述二重积分当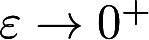 时的极限答案:解析:
时的极限答案:解析: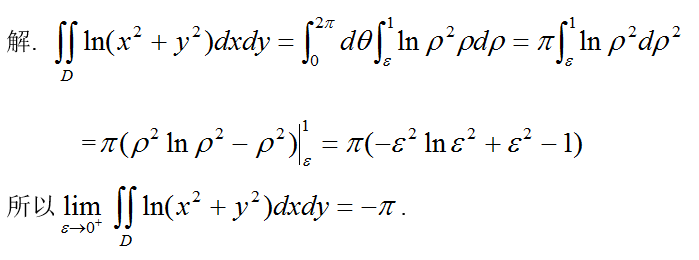
-
第7题:
将二重积分 化为极坐标形式的累次积分, 其中:
化为极坐标形式的累次积分, 其中:  答案:解析:
答案:解析:
-
第8题:
计算二重积分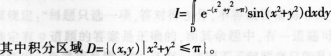 答案:解析:
答案:解析:
-
第9题:
二阶系统是指()
- A、含有二阶微分方程
- B、含有二重积分方程
- C、含有变量的二次方
- D、含有两种不同变量
正确答案:A -
第10题:
当被积函数为常数函数k时,二重积分就是被积区域面积的k倍。
正确答案:正确 -
第11题:
设D={(x,y)|1≤x2+y2≤4},则二重积分的值是().
- A、3π
- B、4π
- C、5π
- D、14/3π
正确答案:D -
第12题:
判断题二重积分化为累次积分后,累次积分的积分上限必须大于积分下限。A对
B错
正确答案: 错解析: 暂无解析 -
第13题:
若D是由x=0,y=0,x2+y2=1所围成在第一象限的区域,则二重积分
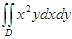
等于( )。
 答案:B解析:采用极坐标法求二重积分,具体计算如下:
答案:B解析:采用极坐标法求二重积分,具体计算如下:
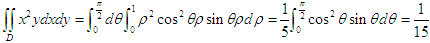
-
第14题:
设D为2≤x2+y2≤2x所确定的区域,则二重积分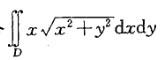 化为极坐标系下的二次积分时等于:
化为极坐标系下的二次积分时等于:
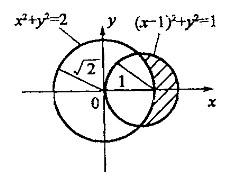
 答案:D解析:提示:画出积分区域D的图形,由x2+y2≥2得知在圆x2+y2=2的外部,由x2+y2≤2x 得知在圆(x-1)2+y2=1的内部,D为它们的公共部分,如图画斜线部分。求交点,解方程组
答案:D解析:提示:画出积分区域D的图形,由x2+y2≥2得知在圆x2+y2=2的外部,由x2+y2≤2x 得知在圆(x-1)2+y2=1的内部,D为它们的公共部分,如图画斜线部分。求交点,解方程组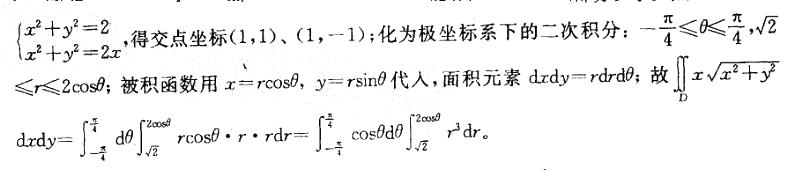
-
第15题:
设二重积分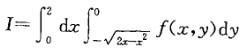 ,交换积分次序后,则I等于:
,交换积分次序后,则I等于:
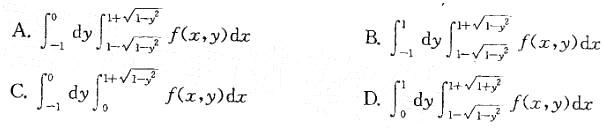 答案:A解析:解:本题考查二重积分交换积分次序方面的知识。解这类题的基本步骤:通过原积分次序画出积分区域的图形,得到积分区域;然后写出先x后y的积分表达式。
答案:A解析:解:本题考查二重积分交换积分次序方面的知识。解这类题的基本步骤:通过原积分次序画出积分区域的图形,得到积分区域;然后写出先x后y的积分表达式。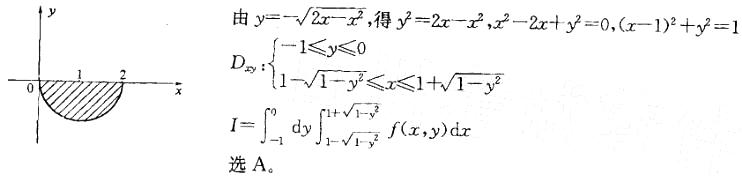
-
第16题:
化二次积分
为极坐标系下的二次积分( )。 答案:D解析:
答案:D解析:
-
第17题:
将二重积分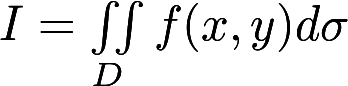 化为极坐标形式的累次积分, 其中: D:
化为极坐标形式的累次积分, 其中: D:  答案:解析:
答案:解析:
-
第18题:
计算二重积分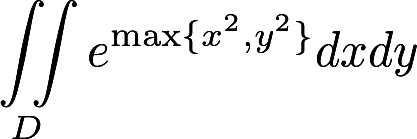 ,其中
,其中 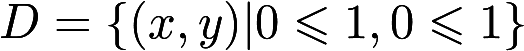 答案:解析:
答案:解析:
-
第19题:
设区域 ,计算二重积分
,计算二重积分 答案:解析:
答案:解析:
-
第20题:
将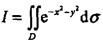 (其中D:x2+y2≤1)化为极坐标系下的二次积分,其形式为( )。
(其中D:x2+y2≤1)化为极坐标系下的二次积分,其形式为( )。
 答案:D解析:提示:
答案:D解析:提示: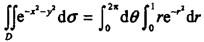 。
。 -
第21题:
二重积分化为累次积分后,累次积分的积分上限必须大于积分下限。
正确答案:正确 -
第22题:
设D={(x,y)||x|≤1,|y|≤1},则二重积分的值是().
- A、2/3
- B、4/3
- C、2
- D、8/3
正确答案:D -
第23题:
若被积区域是若干互不相交的部分区域的和时,则二重积分的值是各个部分区域上重积分的值的()。
- A、积
- B、商
- C、和
- D、差
正确答案:C
