设y＝ln（sinx），则二阶导数y″等于（　　）。

题目
设y＝ln（sinx），则二阶导数y″等于（　　）。

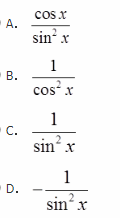
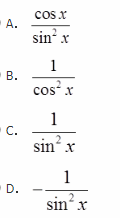
相似考题

1.设y=ln(1＋sinx),求y'。

2.设y=(1+x)1/x，则y‘(1)等于： A. 2 B. e C. 1、2-ln2 D. 1-ln4

3.设函数y=sinx，则y"=_____．

4.若u=xy十y3,则u对y的二阶偏导数为()。

更多“设y＝ln（sinx），则二阶导数y″等于（　　）。”相关问题

  • 第1题：

    设函数y=ln(1+x)，则y"=_____．


    答案：
    解析：

  • 第2题：

    设y=f(x)在(a，6)内有二阶导数，且，f″＞0，则曲线y=f(x)在(a，6)内().

    A.凹
    B.凸
    C.凹凸性不可确定
    D.单调减少

    答案：A
    解析：
    本题考查的知识点为利用二阶导数符号判定曲线的凹凸性.由于在(a，6)区间内f″(x)＞0，可知曲线y=f(x)在(a，6)内为凹的，因此选A.

  • 第3题：

    设f(x)具有二阶导数，y=f(x2),则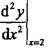的值为()。


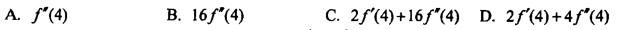    答案：C
    解析：
    正确答案是C。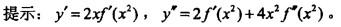

  • 第4题：

    设y=cosx，则y′′=( )

    A.sinx
    B.cosx
    C.-cosx
    D.-sinx

    答案：C
    解析：
    【考情点拨】本题考查了函数的二阶导数的知识点.【应试指导】y=cosx，y'=-sinx，y''=-cosx.

  • 第5题：

    若y=ln2x，则其导数为1/x。


    正确答案:正确

  • 第6题：

    单选题
    设z=f（x2+y2），其中f具有二阶导数，则等于（）．
    A

    2f’（x2+y2）

    B

    4x2f（x2+y2）

    C

    2’（x2+y2）+4x2f（x2+y2）

    D

    2xf（x2+y2）


    正确答案： A
    解析： 暂无解析

  • 第7题：

    单选题
    设函数φ（x）具有二阶连续导数且φ（0）＝0，并且已知yφ（x）dx＋[sinx－φ（x）]dy＝0是一个全微分方程，则φ（x）＝（　　）。
    A

    －e－x/2＋（cosx）/2＋（sinx）/2

    B

    x3－x2/2＋1

    C

    x2ex－2

    D

    （xcosx）/2＋C1cosx＋C2sinx


    正确答案： B
    解析：
    由于yφ（x）dx＋[sinx－φ（x）]dy＝0是一个全微分方程，故∂Q/∂x＝∂P/∂y即cosx－φ′（x）＝φ（x）。即φ′（x）＋φ（x）＝cosx。解此一阶微分方程得φ（x）＝ce－x＋（cosx）/2＋（sinx）/2。又φ（0）＝0，代入上式得c＝－1/2，故φ（x）＝－e－x/2＋（cosx）/2＋（sinx）/2。

  • 第8题：

    填空题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。

    正确答案： 1
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第9题：

    单选题
    设z＝yφ（x/y），其中φ（u）具有二阶连续导数，则∂2z/（∂x∂y）等于（　　）。[2017年真题]
    A

    （1/y）φ″（x/y）

    B

    （－x/y2）φ″（x/y）

    C

    1

    D

    φ′（x/y）－（x/y）φ″（x/y）


    正确答案： B
    解析：
    计算得
    ∂z/∂x＝y·φ′（x/y）·（1/y）＝φ′（x/y）
    ∂2z/∂x∂y＝－（x/y2）φ″（x/y）

  • 第10题：

    单选题
    设y＝ln（cosx），则微分dy等于（　　）。[2012年真题]
    A

    dx/cosx

    B

    cotxdx

    C

    －tanxdx

    D

    －dx/（cosxsinx）


    正确答案： C
    解析：
    等式两边同时微分，得：dy＝f′（x）dx＝（－sinx）dx/cosx＝－tanxdx。

  • 第11题：

    填空题
    设z＝f（x，xy）二阶偏导数连续，则∂2z/∂x∂y＝____。

    正确答案： f2′+xf12″+xyf22″
    解析：
    ∂z/∂x＝f1′＋yf2′，∂2z/（∂x∂y）＝f11″·0＋xf12″＋f2′＋yf22″·x＝xf12″＋f2′＋xyf22″

  • 第12题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    1

    B

    2

    C

    3

    D

    4


    正确答案： C
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第13题：

    设y＝ln（sinx），则二阶导数y″等于（　　）。


    答案：D
    解析：
    函数y＝lnx，则y′＝1/x。因此，y＝ln（sinx）时，根据复合函数求导的链式法则，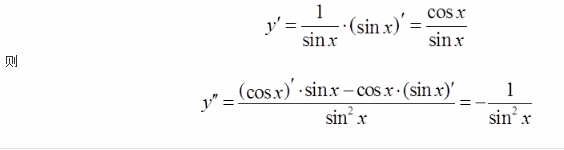

  • 第14题：

    设y=ln（cosx），则微分dy等于：


    答案：C
    解析：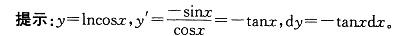

  • 第15题：

    设Y=sinx+COSx，则dy等于()．

    A.(cosx+sinx)dx
    B.(-cosx+sinx)dx
    C.(cosx-sinx)dx
    D.(-cosx-sinx)dx

    答案：C
    解析：
    由微分的基本公式及四则运算法则可得因此选C．

  • 第16题：

    函数y=ax+b的二阶导数等于（）。

    • A、a
    • B、b
    • C、0
    • D、1

    正确答案:C

  • 第17题：

    设z=f（x2+y2），其中f具有二阶导数，则等于（）．

    • A、2f’（x2+y2）
    • B、4x2f"（x2+y2）
    • C、2’（x2+y2）+4x2f"（x2+y2）
    • D、2xf"（x2+y2）

    正确答案:C

  • 第18题：

    单选题
    设函数ψ（x）具有二阶连续导数，且ψ（0）＝ψ′（0）＝0，并已知yψ（x）dx＋[sinx－ψ′（x）]dy＝0是一个全微分方程，则ψ（x）等于（　　）。
    A

    （xsinx）/2

    B

    x3－x2/2

    C

    x2ex

    D

    （xsinx）/2＋C1cosx＋C2sinx


    正确答案： A
    解析：
    由于yψ（x）dx＋[sinx－ψ′（x）]dy＝0是一个全微分方程，则∂Q/∂x＝∂P/∂y，ψ″（x）＋ψ（x）＝cosx。从选项的结构中，可以看出，B、C项无正余弦，一定不是ψ″（x）＋ψ（x）＝cosx的特解，又因为（xsinx）/2＋C1cosx＋C2sinx中含有自由常数，故D项不是特解。将A项代入ψ″（x）＋ψ（x）＝cosx，等式两边相等，故A项是该方程特解。

  • 第19题：

    单选题
    设f有二阶偏导数，z＝f（xy），则∂2z/∂x∂y等于（　　）。
    A

    yf″＋f′

    B

    xy2f″

    C

    xyf′f″

    D

    f′＋xyf″


    正确答案： B
    解析：
    ∂z/∂x＝yf′，∂2z/∂x∂y＝f′＋yf″·x＝f′＋xyf″。

  • 第20题：

    填空题
    设u＝sinx＋φ（sinx＋cosy）（φ为可微函数），且当x＝0时，u＝sin2y，则∂u/∂y＝____。

    正确答案： 2(sinxsiny+cosysiny)
    解析：
    由于x＝0，u＝sin2y，则代入u＝sinx＋φ（sinx＋cosy）中，得sin2y＝φ（cosy）＝1－cos2y，即φ（v）＝1－v2。则φ′（v）＝－2v。故有∂u/∂y＝φ′（sinx＋cosy）（－siny）＝（－2sinx－2cosy）（－siny）＝2（sinxsiny＋cosysiny）。

  • 第21题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    ln1

    B

    0

    C

    sin1

    D

    1


    正确答案： A
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第22题：

    问答题
    设z＝f（x2－y2，exy），其中f具有连续二阶偏导数，求∂z/∂x，∂z/∂y。

    正确答案：
    由复合函数的求导法则,得∂z/∂x=2xf1′+yexyf2′,∂z/∂y=-2yf1′+xexyf2′。
    解析： 暂无解析

  • 第23题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    e


    正确答案： B
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第24题：

    判断题
    若y=ln2x，则其导数为1/x。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

相关内容