平板A以匀速v沿水平直线向右运动；质量为m、半径为r的均质圆轮B，在平板上以匀角速ω以顺时针方向沿水平直线滚而不滑（如图所示）。则圆轮的动能TB的表达式为下列哪一式？

题目
平板A以匀速v沿水平直线向右运动；质量为m、半径为r的均质圆轮B，在平板上以匀角速ω以顺时针方向沿水平直线滚而不滑（如图所示）。则圆轮的动能TB的表达式为下列哪一式？


相似考题

1.质量为m，半径为R的均质圆轮，绕垂直于图面的水平轴O转动，其角速度为w。在图示瞬时，角加速度为0，轮心C在其最低位置，此时将圆轮的惯性力系向O点简化， 其惯性力主矢和惯性力主矩的大小分别为：

2.图示均质圆轮，质量为m，半径为r，在铅垂图面内绕通过圆盘中心O的水平轴转动，角速度为ω，角加速度为ε，此时将圆轮的惯性力系向O点简化，其惯性力主矢和惯性力主矩的大小分别为（　　）。

3.边长为L的均质正方形平板，位于铅垂平面内并置于光滑水平面上，如图所示。若给平板一微小扰动，使其从图示位置开始倾倒，平板在倾倒过程中，其质心C点的运动轨迹是：A.铅垂直线 B.半径为L/2的圆弧 C.抛物线 D.椭圆曲线

4.均质细直杆AB长为l，质量为m，以匀角速度ω绕O轴转动，如图所示，则AB杆的动能为：

更多“平板A以匀速v沿水平直线向右运动；质量为m、半径为r的均质圆轮B，在平板上以匀角速ω以顺时针方向沿水平直线滚而不滑（如图所示）。则圆轮的动能TB的表达式为下列哪一式？ ”相关问题

  • 第1题：

    忽略质量的细杆OC=l，其端部固结匀质圆盘。杆上点C为圆盘圆心。盘质量为m，半径为r。系统以角速度ω绕轴O转动，如图所示。系统的动能是：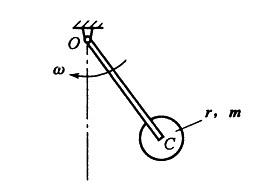



    答案：D
    解析：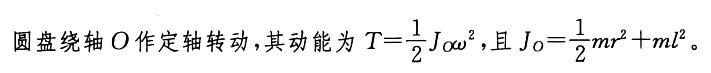

  • 第2题：

    半径为R、质量为m的均质圆轮沿斜面做纯滾动如图所示。已知轮心C的速度为v、加速度为a，则该轮的动能为：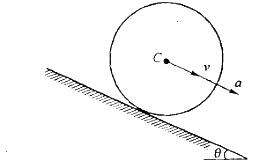



    答案：C
    解析：

  • 第3题：

    图示均质圆轮，质量m，半径R，由挂在绳上的重为W的物块使其绕质心轴O转动。设重物的速度为v，不计绳重，则系统动量、动能的大小是（　　）。




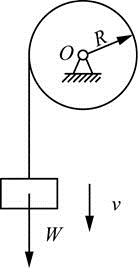
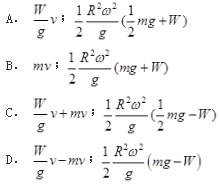    答案：A
    解析：

  • 第4题：

    一半径为r的圆盘以匀角速ω在半径为R的圆形曲面上作纯滚动（如图所示）， 则圆盘边缘上图示M点加速度aM的大小为：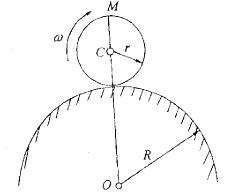



    答案：B
    解析：

  • 第5题：

    如图所示，曲柄OA长R，以匀角速度ω绕O轴转动，均质圆轮B在水平面上做纯滚动，其质量为m，半径为r。在图示瞬时，OA杆铅直。圆轮B对接触点C的动量矩为（　　）mRrω。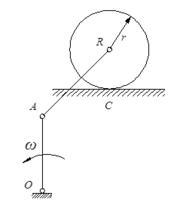

    A．0.5
    B．1.0
    C．1.5
    D．2.0

    答案：B
    解析：
    图示瞬时，点A和点B的速度方向均沿水平方向， AB杆作平动，圆轮B的轮心速度

  • 第6题：

    如图所示，在光滑水平地面上，一质量为M的物体以v0的速度做匀速直线运动，把另一质量为m的物体轻放在M上，由于物体间的摩擦作用，经t秒后两者以共同速度运动。求：
    （1）两物体共同运动速度的大小v；
    （2）在时间t内，m所受摩擦力的大小。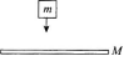


    答案：
    解析：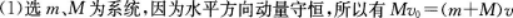


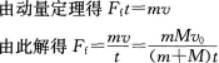
  • 第7题：

    图4-67示均质圆轮，质量为m,半径为r，在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为（ ）。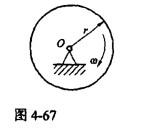



    答案：A
    解析：
    提示：根据动量、动量矩、动能的定义，刚体作定轴转动时，ρ = mvc、LO= JOω, T=1/2JOω2。

  • 第8题：

    阿基米德螺旋线是指一动点沿等速旋转的圆半径方向作（）时该点的运动轨迹。

    • A、匀速直线运动
    • B、匀加速运动
    • C、变速直线运动
    • D、匀减速直线运动

    正确答案:A

  • 第9题：

    圆轮沿直线轨道作纯滚动，只要轮心作匀速运动，则轮缘上任意一点的加速度的方向均指向轮心。


    正确答案:正确

  • 第10题：

    一质量为P的鼓轮，其外圆直径D=200mm，内圆直径d=180mm，放在倾角θ=30°的斜面上，在内圆上绕一绳以大小等于5P的力F平行于斜面向上拉。已知斜面与鼓轮间的静滑动摩擦因数fs=0.5，滚动摩阻系数δ=0.25mm，则此时鼓轮的运动状态为（）

    • A、静止于斜面
    • B、沿斜面又滚又滑
    • C、沿斜面做纯滑动
    • D、沿斜面做纯滚动

    正确答案:B

  • 第11题：

    质量为m的物块A，置于与水平面成θ角的斜面B上，如图所示。A与B间的摩擦系数为f，为保持A与B —起以加速度a水平向右运动，则所需的加速度a至少是：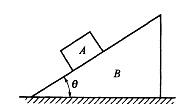



    答案：C
    解析：
    提示：可在A上加一水平向左的惯性力，根据达朗贝尔原理，物块A上作用的重力mg、法向约束力FN、摩擦力F以及大小为ma的惯性力组成平衡力系，沿斜面列平衡方程，当摩擦力F=macosθ+mgsinθ≤FNf(FN = mgcosθ-masinθ)时可保证A与B —起以加速度a水平向右运动。

  • 第12题：

    匀质圆轮重力为W，其半径为r，轮上绕以细绳，绳的一端固定于A点，如图所示。当圆轮下降时，轮心的加速度ac和绳子的拉力T的大小分别为：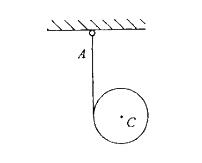



    答案：A
    解析：
    提示：应用平面运动微分方程得:Jcα=Mc(F)；mac=∑F。

  • 第13题：

    如图，半径为R的圆轮以匀角速度作纯滚动，带动AB杆绕B作定轴转动，D是轮与杆的接触点，如图所示。若取轮心C为动点，杆BA为动坐标系，则动点的牵连速度为（　　）。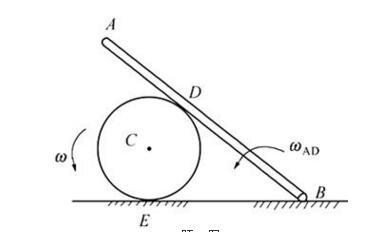


    答案：C
    解析：

  • 第14题：

    小车沿水平方向向右做加速运动，其加速度a0=49.2cm/s2，在小车上有一轮绕O轴转动，转动规律为φ=t2(t以秒计，φ以弧度计)。当t=1s时．轮缘上点A的位置如图所示。如轮的半径r=20cm，求此时点A的绝对加速度aA为( )cm/s2。



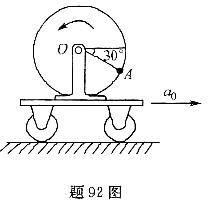
    A．24.7
    B．43.5
    C．68.2
    D．74.6


    答案：D
    解析：
    牵连运动为平动

  • 第15题：

    图示均质圆轮，质量为m，半径为r，在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为：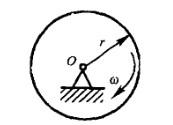



    答案：A
    解析：
    提示：根据动量、动量矩、动能的定义，刚体做定轴转动时p=mvc， LO=JOω，T=1/2JOω2。

  • 第16题：

    半径为R、质量为m的均质圆轮沿斜面作纯滚动如图4-75所示。已知轮心C的速度为V、加速度为a,则该轮的动能为（ ）。

    A. 1/2mv2 B. 3/2mv2 C. 3/4mv2 D. 1/4mv2


    答案：C
    解析：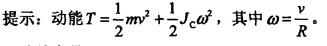

  • 第17题：

    轮圈半径为R，其质量M均匀分布在轮缘上，长为R，质量为m的均质辐条固定在轮心和轮缘间，辐条共有2N根。今若将辐条数减少N根，但保持轮对通过轮心、垂直于轮平而轴的转动惯量保持不变，则轮罔的质量应为（）。



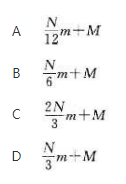    答案：D
    解析：

  • 第18题：

    阿基米德螺旋线是指：动点沿等速旋转的圆半径方向作（）时该点的运动轨迹。

    • A、匀速直线运动
    • B、匀加速运动
    • C、变速直线运动
    • D、匀减速直线运动

    正确答案:A

  • 第19题：

    质量为M的车以速度v0沿光滑水平地面直线前进，车上的人将一质量为m的物体相对于车以速度u竖直上抛，则此时车的速度v＝（）.


    正确答案:V0

相关内容