从均值为μ,方差为σ2(有限)的任意一个总体中抽取样本容量为n的样本,下列说法正确的是( )。A.当n充分大时,样本均值图.png的分布近似服从正态分布B.只有当n C.样本均值图.png的分布与n无关D.无论n多大,样本均值图.png的分布都为非正态分布
题目
B.只有当n <30时,样本均值图.png的分布近似服从正态分布
C.样本均值图.png的分布与n无关
D.无论n多大,样本均值图.png的分布都为非正态分布
相似考题
更多“从均值为μ,方差为σ2(有限)的任意一个总体中抽取样本容量为n的样本,下列说法正确的是( )。 A.当n充分大时,样本均值图.png的分布近似服从正态分布 B.只有当n C.样本均值图.png的分布与n无关 D.无论n多大,样本均值图.png的分布都为非正态分布”相关问题
-
第1题:
下列表述中正确的有( )。A.总体均值的置信区间都是由样本均值加减估计误差得到
B.在小样本情况下,对总体均值的估计都是建立在总体服从正态分布的假定条件下
C.当样本量n充分大时,样本均值的分布近似服从正态分布
D.当总体服从正态分布时,无论样本量大小,样本均值一定服从正态分布
E.对总体均值进行区间估计时,不需要考虑总体方差是否已知答案:A,B,D解析:选项C错误,若总体为未知的非正态总体,当样本量n充分大时,样本均值的分布近似服从正态分布;选项E错误,对总体均值进行区间估计时,需要考虑总体方差是否已知,当总体方差未知时,需要用样本方差来代替总体方差。 -
第2题:
当总体为未知的非正态分布时,只要样本容量n足够大(通常要求n≥30),
样本均值X仍会接近正态分布,其分布的期望值为总体均值,方差为总体方差的1/n。()答案:对解析: -
第3题:
下面几个关于样本均值分布的陈述中,正确的是( )。
Ⅰ.当总体服从正态分布时,样本均值一定服从正态分布
Ⅱ.当总体服从正态分布时,只要样本容量足够大,样本均值就服从正态分布
Ⅲ.当总体不服从正态分布时,无论样本容量多大,样本均值都不会近似服从正态分布
Ⅳ.当总体不服从正态分布时,在小样本情况下,样本均值不服从正态分布
A、Ⅰ.Ⅱ.Ⅲ
B、Ⅰ.Ⅱ
C、Ⅰ.Ⅱ.Ⅳ
D、Ⅰ.Ⅳ答案:D解析:
-
第4题:
下面几个关于样本均值分布的陈述中,正确的是( ) Ⅰ.当总体服从正态分布时,样本均值一定服从正态分布 Ⅱ.当总体服从正态分布时,只要样本容量足够大,样本均值就服从正态分布 Ⅲ.当总体不服从正态分布时,无论样本容量多大,样本均值都不会近似服从正态分布 Ⅳ.当总体不服从正态分布时,在小样本情况下,样本均值不服从正态分布A.Ⅰ.Ⅱ.Ⅲ
B.Ⅰ.Ⅱ
C.Ⅰ.Ⅱ.Ⅳ
D.Ⅰ.Ⅳ答案:D解析:由中心极限定理可知:当总体服从正态分布时,样本均值一定服从正态分布,即时,而若总体为未知的分布时。只要样本容量n足够大(通常要求大于等于30),样本均值仍会接近正其分布的期望值为总体均值,方差为总体方差的1/n.如果总体不是正态分布,当n为小样本时(通常n小于30).样本均值的分布则不服从正态分布。 -
第5题:
中心极限定理表明,若容量为n 的样本来自非正态总体,则样本均值的抽样分布为()
- A、正态分布
- B、只有当n<30时,为正态分布
- C、只有当n≥30时,为正态分布
- D、非正态分布
正确答案:C -
第6题:
如果总体不是正态分布,当n为小样本时(通常n<30),则样本均值的分布服从正态分布。
正确答案:错误 -
第7题:
下列表述中,错误的是()。
- A、总体均值的置信区间都是由样本均值加减估计误差得到
- B、在小样本情况下,对总体均值的估计都是建立在总体服从正态分布的假定条件下
- C、当样本量n充分大时,样本均值的分布近似服从正态分布
- D、当总体服从正态分布时,样本均值不服从正态分布
- E、A总体均值进行区间估计时,不需要考虑总体方差是否已知
正确答案:D,E -
第8题:
关于中心极限定理的描述正确的是:()。
- A、对于n个相互独立同分布的随机变量共同服从正态分布,则样本均值又仍为正态分布
- B、正态样本均值服从分布N(μ,σ2/n)
- C、设X1,X2,„,Xn为n个相互独立共同分布随机变量,其共同分布不为正态分布或未知,但其均值和方差都存在,则在n相当大时,样本均值近似服从正态分布
- D、无论共同分布是什么,只要变量个数n相当大时,均值的分布总近似于正态分布
正确答案:A,B,C,D -
第9题:
单选题关于中心极限定理,下列说法正确的是( )。A多个随机变量的平均值(仍然是一个随机变量)服从或近似服从正态分布
Bn个相互独立同分布随机变量,其共同分布不为正态分布或未知,但其均值μ和方差σ2都存在,则在n相当大的情况下,样本均值X—近似服从正态分布N(μ,σ2/n)
C无论什么分布(离散分布或连续分布,正态分布或非正态分布),其样本均值X—的分布总近似于正态分布
D设n个分布一样的随机变量,假如其共同分布为正态分布N(μ,σ2),则样本均值X—仍为正态分布,其均值不变仍为μ,方差为σ2/n
正确答案: C解析:
AC两项成立的前提条件是多个随机变量必须相互独立且同分布;D项要求这些随机变量相互独立。 -
第10题:
单选题下列由中心极限定理得到的有关结论中,正确的是()。A只有当总体服从正态分布时,样本均值才会趋于正态分布
B只要样本容量n充分大,随机事件出现的频率就等于其概率
C无论样本容量n如何,二项分布概率都可以用正态分布近似计算
D不论总体服从何种分布,只要样本容量n充分大,样本均值趋于正态分布
正确答案: A解析: 暂无解析 -
第11题:
单选题下面几个关于样本均值分布的陈述中,正确的是()。 Ⅰ 当总体服从正态分布时,样本均值一定服从正态分布 Ⅱ 当总体服从正态分布时,只要样本容量足够大,样本均值就服从正态分布 Ⅲ 当总体不服从正态分布时,样本均值一定服从正态分布 Ⅳ 当总体不服从正态分布时,无论样本容量多大,样本均值都不会近似服从正态分布 V 当总体不服从正态分布时,在小样本情况下,样本均值不服从正态分布AI、Ⅳ
BI、V
CⅡ、Ⅲ
DⅡ、V
正确答案: C解析: 由中心极限定理可知:当总体服从正态分布时,样本均值一定服从正态分布,即X~N(μ,σ2)时,X~N(μ,σ2/n)当总体为未知的分布时,只要样本容量n足够大(通常要求n ≥30),样本均值X仍会接近正态分布,其分布的期望值为总体均值,方差为总体方差的1/n;如果总体不是正态分布,当n为小样本时(通常n<30),样本均值的分布则不服从正态分布。 -
第12题:
单选题从均值为μ,方差为σ2的任意一个总体中抽取大小为n的样本,则()A当n充分大时,样本均值的分布近似服从正态分布
B只有当n<30时,样本均值的分布近似服从正态分布
C样本均值的分布与n无关
D无论n多大,样本均值的分布都是非正态分布
正确答案: D解析: 暂无解析 -
第13题:
当总体为未知的非正态分布时,当样本容量n足够大(通常要求n≥30)时,
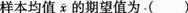 A.总体均值
A.总体均值
B.总体均值的1
C.总体均值的l/√n
D.总体均值的N-n/N-1答案:A解析: -
第14题:
如果总体不是正态分布,当n为小样本时(通常n<30),则样本均值的分布服从正态分布。( )答案:错解析: -
第15题:
下面几个关于样本均值分布的陈述中,正确的是( )。
Ⅰ.当总体服从正态分布时,样本均值一定服从正态分布
Ⅱ.当总体服从正态分布时,只要样本容量足够大,样本均值就服从正态分布
Ⅲ.当总体不服从正态分布时,样本均值一定服从正态分布
Ⅳ.当总体不服从正态分布时,无论样本容量多大,样本均值都不会近似服从正态分布
Ⅴ.当总体不服从正态分布时,在小样本情况下,样本均值不服从正态分布
A、Ⅰ.Ⅴ
B、Ⅰ.Ⅱ.Ⅲ.Ⅳ
C、Ⅰ.Ⅱ.Ⅳ
D、Ⅱ.Ⅲ.Ⅳ答案:A解析:
-
第16题:
下面儿个关于样本均值分布的陈述中,正确的是( )。A: 当总体服从正态分布时,样本均值一定服从正态分布
B: 当总体服从正态分布时,只要样本容量足够人,样本均值就服从止志分布
C: 当总体不服从止志分布时,样本均值一定服从正态分布
D: 当总体不服从正态分布时,无论样本容量多大,样本均值都不会近似服从正态分布
E: 当总体不服从正态分布时,在小样本情况下,样本均值不服从正态分布答案:A,E解析:
-
第17题:
从均值为μ,方差为σ2的任意一个总体中抽取大小为n的样本,则()
- A、当n充分大时,样本均值的分布近似服从正态分布
- B、只有当n<30时,样本均值的分布近似服从正态分布
- C、样本均值的分布与n无关
- D、无论n多大,样本均值的分布都是非正态分布
正确答案:A -
第18题:
当总体为未知的非正态分布时,只要样本容量n足够大(通常要求n≥30),样本均值Untitled-1_clip_image020_0001.gif仍会接近正态分布,其分布的期望值为总体均值,方差为总体方差的1/n。
正确答案:正确 -
第19题:
下列由中心极限定理得到的有关结论中,正确的是()。
- A、只有当总体服从正态分布时,样本均值才会趋于正态分布
- B、只要样本容量n充分大,随机事件出现的频率就等于其概率
- C、无论样本容量n如何,二项分布概率都可以用正态分布近似计算
- D、不论总体服从何种分布,只要样本容量n充分大,样本均值趋于正态分布
正确答案:D -
第20题:
多选题下列说法错误的是()A总体均值的置信区间都是由样本均值加减估计误差得到
B在小样本情况下,对总体均值的估计都是建立在总体服从正态分布的假定条件下
C当样本量n充分大时,样本均值的分布近似服从正态分布
D当总体服从正态分布时,样本均值不服从正态分布
E对总体均值进行区间估计时,不需要考虑总体方差是否已知
正确答案: D,B解析: -
第21题:
多选题关于中心极限定理的描述正确的是:()。A对于n个相互独立同分布的随机变量共同服从正态分布,则样本均值又仍为正态分布
B正态样本均值服从分布N(μ,σ2/n)
C设X1,X2,„,Xn为n个相互独立共同分布随机变量,其共同分布不为正态分布或未知,但其均值和方差都存在,则在n相当大时,样本均值近似服从正态分布
D无论共同分布是什么,只要变量个数n相当大时,均值的分布总近似于正态分布
正确答案: C,D解析: 暂无解析 -
第22题:
多选题下列表述中,错误的是( )。A总体均值的置信区间都是由样本均值加减估计误差得到
B在小样本情况下,对总体均值的估计都是建立在总体服从正态分布的假定条件下
C当样本量n充分大时,样本均值的分布近似服从正态分布
D当总体服从正态分布时,样本均值不服从正态分布
E对总体均值进行区间估计时,不需要考虑总体方差是否已知
正确答案: C,B解析:
当总体服从正态分布时,样本均值也服从正态分布。对总体均值进行区间估计时,需要分两种情况:方差已知和方差未知。 -
第23题:
判断题当总体为未知的非正态分布时,只要样本容量n足够大(通常要求n≥30),样本均值Untitled-1_clip_image020_0001.gif仍会接近正态分布,其分布的期望值为总体均值,方差为总体方差的1/n。A对
B错
正确答案: 错解析: 暂无解析
