经过A(0,1),B(1,2),C(2,3)的插值多项式P(x)=()A、xB、x+1C、2x+1D、x^2+1
题目
经过A(0,1),B(1,2),C(2,3)的插值多项式P(x)=()
A、x
B、x+1
C、2x+1
D、x^2+1
相似考题
参考答案和解析
参考答案:D
更多“经过A(0,1),B(1,2),C(2,3)的插值多项式P(x)=() A、xB、x+1C、2x+1D、x^2+1”相关问题
-
第1题:
依据3个样点(0,1),(1,2)(2,3),其插值多项式p(x)为()
A、x
B、x+1
C、x-1
D、x+2
参考答案:B
-
第2题:
设X,Y相互独立,且X~N(1,2),Y~N(0,1),求2=2X-Y+3的密度函数,答案:解析:【解】因为X,Y相互独立且都服从正态分布,所以X,Y的线性组合仍服从正态分布,即2=2X-Y+3服从正态分布,由E(Z)=2E(X)-E(Y)+3=5,D(Z)=4D(X)+D(Y)=9,则Z的密度函数为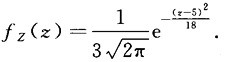
-
第3题:
设服从N(0,1)分布的随机变量X,其分布函数为φ(x),如果φ(1)=0.84,则P|x|≤1的值是( )。
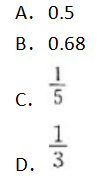 答案:B解析:X~N(0,1),P{|x|≤1)=2Φ(1)-1=0.68
答案:B解析:X~N(0,1),P{|x|≤1)=2Φ(1)-1=0.68 -
第4题:
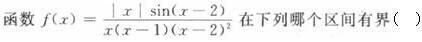 A.(-1,0)
A.(-1,0)
B.(0,1)
C.(1,2)
D.(2,3)答案:A解析: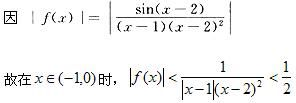
-
第5题:
给定插值点(xi,fi)(i=0,1,...,n)可分别构造Lagrange插值多项式和Newton插值多项式,它们是否相同?为什么?它们各有何优点?
正确答案: 给定插值点后构造的Lagrange多项式为Ln(x)Newton插值多项式为Nn(x)它们形式不同但都满足条件Ln(xi)=fi,Nn(xi)=fi(i=0,1,...,n),于是Ln(xi)-Nn(xi)=0,i=0,1,...,n。它表明n次多项式[Ln(x)-Nn(x)]有n+1个零点,这与n次多项式只有n个零点矛盾,故Ln(x)=Nn(x)即Ln(x)与Nn(x)是相同的。Ln(x)是用基函数表达的,便于研究方法的稳定性和收敛性等理论研究和应用,但不便于计算,而Nn(x)每增加一个插值点就增加一项前面计算都有效,因此较适合于计算。 -
第6题:
设f(0)=0,f(1)=16,f(2)=46,则f[0,1]=(),f[0,1,2]=(),f(x)的二次牛顿插值多项式为()。
正确答案:16;7;0+16(x-0)+7(x-0)(x-1) -
第7题:
在一次试验中,测得(x,y) 的四组值分别是A(1,2),B(2,3),c(3,4),D(4,5) ,则Y与X之间的回归直线方程为()
- A、y=x+1
- B、y=x+2
- C、y=2x+1
- D、y=x-1
正确答案:A -
第8题:
方程x5-3x=1在下列区间内至少有一个实根的区间是().
- A、(0,1)
- B、(1,2)
- C、(2,3)
- D、(3,+∞)
正确答案:B -
第9题:
填空题设f(0)=0,f(1)=16,f(2)=46,则f[0,1]=(),f[0,1,2]=(),f(x)的二次牛顿插值多项式为()。正确答案: 16,7,0+16(x-0)+7(x-0)(x-1)解析: 暂无解析 -
第10题:
单选题经过点A(0,1),B(1,2),C(2,3)的插值多项式P(x)为( )。Ax
Bx+1
C2x十1
D五十1
正确答案: D解析: 暂无解析 -
第11题:
单选题已知两点(2,4)、(4,6),利用插值多项式求点(3,x)中的x为( )。A4.5
B5.0
C4.75
D5.5
正确答案: D解析: 暂无解析 -
第12题:
单选题两个本原多项式g(x)和f(x),令h(x)=g(x)f(x)记作Cs,若h(x)不是本原多项式,则存在p当满足什么条件时使得p|Cs(s=0,1…)成立?()Ap是奇数
Bp是偶数
Cp是合数
Dp是素数
正确答案: C解析: 暂无解析 -
第13题:
设X~N(0,1),则下列各式成立的有( )。
A. P(X>a)=P(X≥a) =1 -Φ(a) B. P(a≤X≤b) =Φ(b) -Φ(a)
C. P( X ≤a) =2Φ(a) -1 D. Φ(-a) = -Φ(a)
E. P(X答案:A,B,C解析:对于标准正态分布有Φ(-a) =1 -Φ(a), P(X -
第14题:
设X1,2X,…,Xn(n>2)相互独立且都服从N(0,1),Yi=Xi-X(i=1,2,…,n).求:
(1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).答案:解析:
-
第15题:
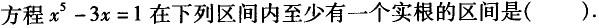 A.(0,1)
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,+∞)答案:B解析:
-
第16题:
两个本原多项式g(x)和f(x),令h(x)=g(x)f(x)记作Cs,若h(x)不是本原多项式,则存在p当满足什么条件时使得p|Cs(s=0,1…)成立?()
- A、p是奇数
- B、p是偶数
- C、p是合数
- D、p是素数
正确答案:D -
第17题:
通过四个互异节点的插值多项式p(x),只要满足(),则p(x)是不超过二次的多项式。
正确答案:满足三阶均差为0 -
第18题:
不属于本原多项式的是()。
- A、x^2-2x
- B、x^2+2x
- C、2x-1
- D、2x-2
正确答案:D -
第19题:
一维数据插值的函数yi=interp1(x,y,xi,’nearest’)表示()。
- A、线性插值
- B、最近点插值
- C、3次多项式插值
- D、3次样条插值
正确答案:B -
第20题:
单选题方程x5-3x=1在下列区间内至少有一个实根的区间是().A(0,1)
B(1,2)
C(2,3)
D(3,+∞)
正确答案: B解析: 暂无解析 -
第21题:
问答题给定插值点(xi,fi)(i=0,1,...,n)可分别构造Lagrange插值多项式和Newton插值多项式,它们是否相同?为什么?它们各有何优点?正确答案: 给定插值点后构造的Lagrange多项式为Ln(x)Newton插值多项式为Nn(x)它们形式不同但都满足条件Ln(xi)=fi,Nn(xi)=fi(i=0,1,...,n),于是Ln(xi)-Nn(xi)=0,i=0,1,...,n。它表明n次多项式[Ln(x)-Nn(x)]有n+1个零点,这与n次多项式只有n个零点矛盾,故Ln(x)=Nn(x)即Ln(x)与Nn(x)是相同的。Ln(x)是用基函数表达的,便于研究方法的稳定性和收敛性等理论研究和应用,但不便于计算,而Nn(x)每增加一个插值点就增加一项前面计算都有效,因此较适合于计算。解析: 暂无解析 -
第22题:
单选题一维数据插值的函数yi=interp1(x,y,xi,’cubic’)表示()。A线性插值
B最近点插值
C3次多项式插值
D3次样条插值
正确答案: A解析: 暂无解析 -
第23题:
填空题通过四个互异节点的插值多项式p(x),只要满足(),则p(x)是不超过二次的多项式。正确答案: 满足三阶均差为0解析: 暂无解析
