将右边的箔片沿虚线折起来，便可做一个正方体。问这个正方体的3号面对面是几号面？( )A.1B.2C.5D.6
题目
将右边的箔片沿虚线折起来，便可做一个正方体。问这个正方体的3号面对面是几号面？( )
A.1
B.2
C.5
D.6
相似考题
更多“将右边的箔片沿虚线折起来,便可做一个正方体。问这个正方体的3号面对面是几号面?( ) A.1 B.2 C ”相关问题
-
第1题：
有一批边长为1厘米的小正方体，其中一面涂红色的有400个，相邻两面涂红色的有30个，相邻三面涂红色的有1个，其余小正方体各面都没有涂颜色。用这一批小正方体组成一个大正方体，要求这个大正方体有三个面是红色，且这三个面两两相邻，其余的三个面没有颜色。假如没有涂颜色的小正方体数量足够多，那么这个正方体的边长最大是（ ）厘米。A.10
B.11
C.12
D.13答案：B解析：第一步，本题考查几何问题，属于几何构造。
第二步，让三面都涂色的小正方体作为一个顶角，然后与其相相连的三个棱均放置相邻两个面涂色的小正方体，每条棱上各10个，此时需要需要单面涂色的小正方体10×10×3＝300（个），可以满足，故边长最长为10＋1＝11（厘米）。 -
第2题：
连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米，问正八面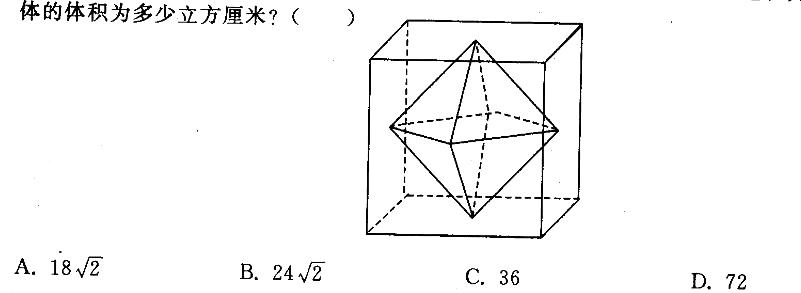
答案：C解析：该正八面体可以看做由两个四棱锥拼成的，每个四棱锥的底面为原正方体四个侧面的中心连线，高分别为上下两个正方体底面中心到四棱锥底面的距离，解得V= 1/3x(62x1/2)X3X2 =36(cm3)。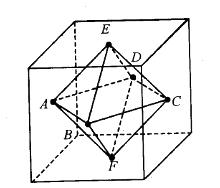
-
第3题：
4、将一个正方体表面涂红，在它的长、宽、高上等距离各切9刀，将得到的1000个小正方体均匀混杂，从这些小正方体中任意取出一个，问取出的小正方体各面都没有红色的概率是_________。（保留四位小数)
解：（1） ；（2） ；（3） 。 本小题主要考查概率等基础知识，考查运算求解能力、应用数学知识分析和解决实际问题的能力．用到的知识点为：概率=所求情况数与总情况数之比，关键是找到相应的具体数目． （1）各个面都没有颜色小正方体是在8个面的中间处，共8个，再根据概率公式解答即可． （2）在大正方体表面且不在棱上及顶点的小正方体只有1个面涂红色， 共24个，因此可知概率值。 （3）三面涂有颜色的小正方体是在8个顶点处，共8个，再根据概率公式解答即可；两面涂有颜色的小正方体是在8条棱的中间处，共24个，再根据概率公式解答即可； 解：（1）在大正方体表面的小正方体没有涂红色共8个 3分 5分 （2）在大正方体表面且不在棱上及顶点的小正方体只有1个面涂红色， 共24个 8分 10分 （3） 13分 -
第4题：
一只蚂蚁从右图的正方体的A顶点沿正方体的表面爬到正方体的C顶点，设正方体边长为a，问该蚂蚁爬过的最短路程为：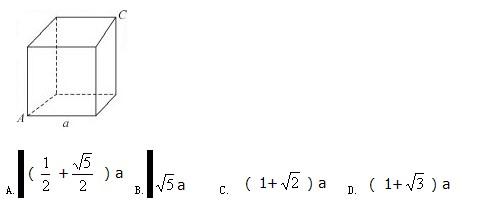
A.A B. B C. C D. D答案：B解析：解题指导： 该最短路程为√[1+﹙22a﹚]=√5a。故答案为B。 -
第5题：
将一个正方体表面涂红，在它的长、宽、高上等距离各切9刀，将得到的1000个小正方体均匀混杂，从这些小正方体中任意取出一个，问取出的小正方体各面都没有红色的概率是_________。（保留四位小数)
解：（1） ；（2） ；（3） 。 本小题主要考查概率等基础知识，考查运算求解能力、应用数学知识分析和解决实际问题的能力．用到的知识点为：概率=所求情况数与总情况数之比，关键是找到相应的具体数目． （1）各个面都没有颜色小正方体是在8个面的中间处，共8个，再根据概率公式解答即可． （2）在大正方体表面且不在棱上及顶点的小正方体只有1个面涂红色， 共24个，因此可知概率值。 （3）三面涂有颜色的小正方体是在8个顶点处，共8个，再根据概率公式解答即可；两面涂有颜色的小正方体是在8条棱的中间处，共24个，再根据概率公式解答即可； 解：（1）在大正方体表面的小正方体没有涂红色共8个 3分 5分 （2）在大正方体表面且不在棱上及顶点的小正方体只有1个面涂红色， 共24个 8分 10分 （3） 13分