在1至100这100个数中，有既不能被5整除也不能被9整除的数，它们的和是( )。A 1 644B．1779C．3406D．3541

题目

在1至100这100个数中，有既不能被5整除也不能被9整除的数，它们的和是( )。

A 1 644

B．1779

C．3406

D．3541

相似考题

1.用0，1，2，3，4这五个数字可以组成（ ）个大于20000且不能被5整除的、没有重复数字的5位数。A．120B．54C．48D．72

2.输出1—100之间不能被12整除的数。

3.1至100中所有不能被9整除的自然数的和是( )。A． 217B．594C．5050D．4456

4.能被2整除的数叫做（ ），不能被2整除的数叫做（ ）。

更多“在1至100这100个数中，有既不能被5整除也不能被9整除的数，它们的和是( )。A 1 644B．1779C．3406D．3541”相关问题

  • 第1题：

    从1，2，3，……，50这五十个数中，取出若干个数，使其中任意两个数的和都不能被7整除，则最多能取多少个数( )。

    A. 21    B. 22C. 23   D. 29


    从0开始，每7个数一组（0——6，7——13，......，42——48，共七组）中，最多可以选4个数（分别是除7余0，1，2，3的数）
    所以，它们之中可以选7*4＝28个数。
    另外：0不包含在其中，要减去1个数；49和50两个数除7的余数分别是0和1，也要计算上，再加2个数。
    故，最多共可取28－1+2＝29个数

  • 第2题：

    现有以下程序： Private Sub Command1 Click（ ） c1=0 c2=0 For i=1 To 100 If i Mod 3=0 Then c1=c1+1 Else If i Mod 7=0 Then c2=c2+1 End If Next i Print c1+c2 End Sub 此程序运行后输出的是在1～100范围内（ ）。

    A.同时能被3和7整除的整数个数

    B.能被3或7整除的整数个数(同时被3和7整除的数只记一次)

    C.能被3整除，而不能被7整除的整数个数

    D.能被7整除，而不能被3整除的整数个数


    正确答案：B
    B。【解析】i是1到100的循环，在程序中，对3和7取模，显然就是3和7的倍数关系。需要注意的是If和else语句分别判断3和7的倍数而同时是21倍数的时候会不计，这有别于传统的计数方法。

  • 第3题：

    在1至100的自然数中，不能被2整除且不能被3整除且不能被5整除的数共有多少个?（ ） A．23个 B．26个 C．27个 D．74个


    正确答案：B

    1至100的自然数中，能被2整除的数有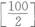=50个，能被3整除的数有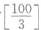=33个，能被5整除的数有=20个，能被2整除且能被3整除的数有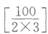＝16个，能被5整除且能被3整除的数有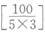＝6个，能被2整除且能被5整除的数有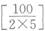＝10个，能被2整除且能被3整除且能被5整除的数有=3个，故由容斥原理，不能被2整除且不能被3整除且不能被5整除的数共有100－[50+33+20－(16+6+10)+3]=26个。故选B。

  • 第4题：

    1、2、3、4、5、6、7、8、9这九个数字各用一次，组成三个能被9整除的三位数，这三个数的和最大是：

    A.2007
    B.2394
    C.2448
    D.2556

    答案：C
    解析：
    第一步，本题考查多位数问题。
    第二步，1—9这九个数字各用一次，先将1—9加和为45，组成三个能被9整除的三位数，可知每个三位数各位数字加和均为9的倍数，则三个三位数各位数字加和分别为9、18、18。
    第三步，要使这三个数的和最大，则每个三位数百位上的数字应尽量大，先考虑和为9的三位数，百位最大为6，这个三位数是621，剩余两个三位数最大分别为954和873，则954＋873＋621＝2448（可用尾数法，尾数为8）。

  • 第5题：

    1-100各数所有不能被9整除的自然数的和是（ ）。

    A. 217
    B. 594
    C. 5050
    D. 4456

    答案：D
    解析：
    在1至100中，被9整除的数的和是：
    9 + 18 + 27+-----+99 = 9X(1+ 2 + 3+----+11) =9 X 66 = 594
    1至100各数之和是： 1+ 2 + 3+----+100 = 5050
    所以在1至100的各数中，所有不能被9整除的数的和是5050-594 = 4456。

  • 第6题：

    从1开始的自然数中，第100个不能被3整除的数是（）。

    A.134
    B.142
    C.149
    D.152

    答案：C
    解析：
    从1开始，每三个数作为一组，每组中前两个数不能被3整除，100÷2=50,因此第100个不能被3整除的数是第50组中的第二个数。3x50=150，第50组数是148、149、150，因此所求是149。

  • 第7题：

    在1至100这100个数中，有既不能被5整除也不能被9整除的数，它们的和是（ ）。
    A. 1644 B. 1779 C. 3406 D. 3541


    答案：D
    解析：
    先求出被5或9整除的数的和。
    1-100中被5整除的数有5，10，15，...，100，和为 5 + 10 + 15+-----+100=(100 + 5) X20 + 2 = 1050。
    1-100中被9整除的数有9，18，…，99，和为 9 + 18 + 27+-----+99= (9 + 99) X 11 + 2 = 594。
    又因为1-100中，45，90这两个数同时被5与9整除，于是所求的和是(1 + 2+-----+100)-(5 +10+-----+100)-(9 + 18+-----+99) +(45 + 90) = 3541。

  • 第8题：

    编写一个Java程序，对于给定的年份，回答“Leap Year”（闰年）或者“Not a Leap Year”（平年）。如果一个年份能被4整除，但是不能被100整除，它是闰年；如果一个年份能被100整除，也能被400整除，它也是闰年。需要定义名为LeapYear的服务提供类

    略

  • 第9题：

    数据结构与算法中，关于素数描述正确的是（）

    • A、素数就是合数
    • B、素数不能被本身整除
    • C、素数又称为质数只能被1和它本身整除
    • D、素数不仅能被1和它本身整除，还能被其它数整除

    正确答案:C

  • 第10题：

    单选题
    数据结构与算法中，关于素数描述正确的是（）
    A

    素数就是合数

    B

    素数不能被本身整除

    C

    素数又称为质数只能被1和它本身整除

    D

    素数不仅能被1和它本身整除，还能被其它数整除


    正确答案： B
    解析： 暂无解析

  • 第11题：

    1~100各数所有不能被整除的自然数的和是( )

    A.594 B.3854 C.4456 D.5050


    正确答案：C
    C. 解析：1-100的总和为100（1+100）/2=5050，9的倍数为9× 1，9 × 2，…，一直到9 × 11，和为9×11（1+11）/2=594，故答案为 5050-594=4456

  • 第12题：

    1～100各数中所有不能被9整除的自然数的和是()。

    A. 217 B. 594 C. 5050 D. 4456


    正确答案：D

    在1至100中，被9整除的数的和是：

    　　9+18+27+…+99

    　　=9×(1+2+3+…+11)

    　　=9×66

    　　=594

    　　1至100各数之和是：

    　　1+2+3+…+100=[100(1+100)]/2=5050

    　　所以在1至100的各数中，所有不能被9整除的数的和是：

    　　5050-594=4456。

    　　因此，本题正确答案为D。

     

  • 第13题：

    六位数442738，能被72整除，且这六个数之和能被9整除，A与B的值为（ ）。

    A．6，5

    B．5，6

    C．7，0

    D．6，2


    正确答案：B
    72—8×9，因此六位数A42738能被8与9整除，所以后三位738能被8整除，故B=6。又由于A+4+2+7+3+B能被9整除，结合选项所以A=5。

  • 第14题：

    1至1000中所有不能被5，6，8整除的自然数有多少个？（）

    A. 491
    B. 107
    C. 400
    D. 600

    答案：D
    解析：
    只要求出1-1000内5的倍数、6的倍数或8的倍数或5X6，5X8，24，120的倍数， 再根据容斥原理就可求得。
    5的倍数有5、10…1000共200个；
    6的倍数有6、12…996共166个；
    8的倍数有8、16…共125个；
    24的倍数有24、48...984共41个；
    30的倍数有30、60…990共33个；
    40的倍数有40、80…1000共25个；
    120的倍数有120、240…960共8个。
    根据容斥原理可知，5或6或8的倍数有：
    (200 + 166 + 125)-(33 + 25+41)+8 = 400（个）。
    不能被5或6或8中任一个整除的有1000-400 = 600（个）。
    故本题选D。

  • 第15题：

    从1到100的整数中任取一个数，则该数能被5或7整除的概率为（ ）

    A.0.02
    B.0.14
    C.0.2
    D.0.32
    E.0.34

    答案：D
    解析：

  • 第16题：

    1～100，这100个自然数中，最多可以选出多少个数，才能保证任意两个数之和都不能被3整除？（）

    A.33
    B.34
    C.35
    D.36

    答案：C
    解析：
    这100个数可以分成三类：①能被3整除的数，共有33个；②被3除余数是1的数，共有34个；③被3除余数是2的数，共有33个。显然，把第②组的数全选出，再从第①组任选一个数，保证任两个数字之和不能被3整除，即最多可以选出34＋1＝35个，故本题选C。

  • 第17题：

    以下程序的功能是：随机生成10～100之间的整数，并统计在1000个这样的整数中，能被5整除的数的个数。
    Int(Rnd*91+10)；C+1
    略

  • 第18题：

    在1和2015之间（包括1和2015在内）不能被4、5、6三个数任意一个数整除的数有（）个。


    正确答案:1075

  • 第19题：

    将条件“y能被4整除但不能被100整除，或y能被400整除”写成逻辑表达式（）。


    正确答案:y%4==0&&y%100!=0||y%400==0

  • 第20题：

    填空题
    在1和2015之间（包括1和2015在内）不能被4、5、6三个数任意一个数整除的数有（）个。

    正确答案： 1075
    解析： 暂无解析

相关内容