从一张1952mm×568mm的长方形纸片上，剪下一个边长尽可能大的正方形，如果剩下的部分不是正方形，那么在剩下的纸片上再剪下一个边长尽可能大的正方形。按照上面的过程不断地重复，最后一共可剪得正方形多少个?（ ） A．8 B．10 C．12 D．14

题目

从一张1952mm×568mm的长方形纸片上，剪下一个边长尽可能大的正方形，如果剩下的部分不是正方形，那么在剩下的纸片上再剪下一个边长尽可能大的正方形。按照上面的过程不断地重复，最后一共可剪得正方形多少个?（ ） A．8 B．10 C．12 D．14

相似考题

1.把一个正方形的一边减少2cm，另一边增加20%，得到一个长方形，它与原来的正方形面积相等，那么，正方形的边长是( )。m。A．13B．10C．12D．15

2.从一块正方形木板上锯下宽5cm的一个木条后，剩下的长方形面积是750cm2,锯下的木条面积是多少平方厘米？ A. 25 B. 150 C. 152 D. 168

3.劳动技能课上老师给出一道手工题：一张正方形纸片，在一对对角处各减去一个边长为1厘米的小正方形（如右图所示），想办法把这个缺角的正方形恰好剪成一些长2厘米、宽1厘米的小矩形，问初始的大正方形边长要多大时，任务才有可能完成 A.8厘米 B.15厘米 C.32厘米 D.以上答案都不对

4.从一块正方形木板上锯下宽5cm的一个木条后，剩下的长方形面积是750cm2,锯下的木条面积是多少平方厘米？A．25B．150C．152D．168

参考答案和解析
正确答案：D
从长1952mm、宽568mm的长方形纸片上首先可剪下边长为568mm的
正方形，这样的正方形的个数恰好是1952除以568所得的商，而余数恰好是剩下的长方形的宽，于是有：1952÷568=3…248，568÷248=2…72，248÷72=3…32，72÷32=2…8，32÷8=4，因此一共可得到正方形3+2+3+2+4=14(个)，故正确答案为D。
更多“从一张1952mm×568mm的长方形纸片上,剪下一个边长尽可能大的正方形,如果剩下的部分不是正方形,那 ”相关问题

  • 第1题：

    如下图所示，一张边长8厘米的正方形纸片先进行对折，再沿着两边的中点连线减掉一个角后，则剩下部分展开面积是多少平方厘米？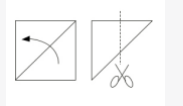

    A.16
    B.32
    C.36
    D.48

    答案：D
    解析：

  • 第2题：

    如图，将正方形边长三等分后可得9个边长相等的小正方形，把中间的小正方形去掉，对剩下的8个小正方形，均按上面方法操作。问：对一个边长为2的正方形如此操作三次后所剩白色区域的面积是多少？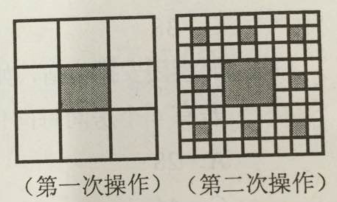

    A.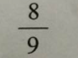
    B.
    C.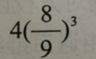
    D.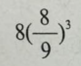

    答案：C
    解析：

  • 第3题：

    3、在一个边长为20cm的正方形纸片上剪下一个最大的圆后，这张正方形纸片还剩下多少平方厘米？


    米；50分游标卡

  • 第4题：

    从一块正方形木板上锯下宽5cm的一个木条后。剩下的长方形面积是750cmz．锯下的木条面积是多少平方厘米?（）
    A.25
    B.150
    C.152
    D.168


    答案：B
    解析：
    根据题意画出下图：

    设正方形的边长为xcm，那么最后剩下的长方形的宽为(x-5)cm，则x(x-5)=750，解得x=30cm，因此锯掉的木条面积为30×5=150c㎡。
    另解，可以直接观察选项，与750的和为完全平方数的即为答案，只有B项满足。

  • 第5题：

    劳动技能课上老师给出一道手工题：一张正方形纸片，在一对对角处各减去一个边长为1厘米的小正方形（如右图所示），想办法把这个缺角的正方形恰好剪成一些长2厘米、宽1厘米的小矩形，问初始的大正方形边长要多大时，任务才有可能完成？

    A.8
    B.15
    C.32
    D.以上答案都不对

    答案：D
    解析：
    将大正方形拆分为若干个边长 1 厘米的小正方形，根据大正方形边长的奇偶性分类讨论如下：
    ①若大正方形的边长为奇数，则小正方形的个数也为奇数，剪去 2 个小正方形后，剩下的小正方形个数依
    然为奇数；而每个小矩形需要占用 2 个小正方形，则剩下的奇数个小正方形不可能全部拆成小矩形，矛盾。故 边长为奇数必然不满足题意，排除 B 项；
    ②若大正方形的边长为偶数，如下图所示：将其拆分为若干个小正方形之后，黑色和白色方块的总数相等， 且拿掉的对角的两个小正方形一定都是黑色或白色，那么剩下的黑色与白色方块数必然不等，此为结论 1。
    观察图形，要取出 2×1 的小矩形，必须由一黑一白组成。那么，要让剩下的图形恰好能分成若干个 2×1 的小矩形，则剩下图形的黑色与白色方块个数必须相等，此为结论 2。
    结论 2 与结论 1 明显矛盾，故边长为偶数也必须不满足题意，排除 A、C 项。 故正确答案为 D。

相关内容