77个连续自然数的和是7546,则其中第45个自然数是()。A. 91B. 100C. 104D. 105
题目
77个连续自然数的和是7546,则其中第45个自然数是()。
A. 91
B. 100
C. 104
D. 105
相似考题
更多“77个连续自然数的和是7546,则其中第45个自然数是()。A. 91 B. 100 C. 104 D. 105 ”相关问题
-
第1题:
100个连续自然数的和是10950,取出其中所有的奇数个数(第1个,第3个,……,第99个),将它们相加,则和为( )。
A.5500
B.5425
C.5525
D.5450
正确答案:D
D[解析]连续自然数相邻两数之差是1,所以第2个数比第1个数大1,第4个数比第3个数大1,……,第100个数比第99个数大1,取出的50个奇数比没取出的50个偶数总共少50,因此所有的奇数之和是:(10950–50)÷2=5450。故本题选D。 -
第2题:
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。【说明】如果一个自然数N恰好等于它所有不同的真因子(即N的约数以及1,但不包括N)之和S,则称该数为“完美数”。例如6=1+2+3,28=1+2+4+7+14,所以6和28都是完美数。显然,6是第1个(即最小的)完美数。下面流程图的功能是求500以内所有的完美数。【流程图】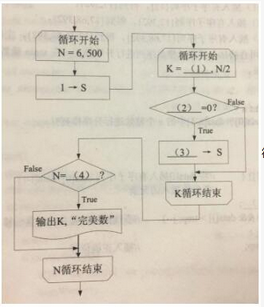
循环开始框中要注明:循环变量=初始值,终值[,步长],步长为1时可以缺省。如果某自然数小于其所有真因子之和(例如24<1+2+3+4+6+8+12),则称该自然数为亏数;如果某自然数大于其所有真因子之和(例如8>1+2+4),则称该自然数为贏数;如果某自然数等于从1开始的若干个连续自然数之和(例如10=1+2+3+4)则称该自然数为三角形数。据此定义,自然数496是( )。供选择答案:A.亏数 B.赢数 C.完美数,非三角形数 D.完美数和三角形数答案:解析:(1)2(2)N%K(3)S+K(4)S(5)D
【解析】
流程图的功能是求500以内所有的完美数,N的值范围是6~500,因此N是需要判断是否为完美数,首先需要求出N的所有真因子,然后再判断N和真因子之和是否相等,从流程图可以看出S是保存真因子和的变量,K是保存真因子的变量,因此K的初始值是2,终值是N/2,因此第(1)空处填写:2;判断K是否为N的真因子,即判断N%K(N除以K取余)是否为0,第(2)空填写:N%K;当K为N的真因子时,需要计算所有K的和,即S=S+K,第(3)空填写:S+K;最后判断N和S是否相等,第(4)空填写:S。496的真因子有:1、2、4、8、16、31、62、124、248,1+2+4+8+16+31+62+124+248=496;因此496是完美数,同时496=(1+2+3+4+……+30+31),因此496是完美数和三角形数。 -
第3题:
以下程序段的功能是()。 int i,s=0; for(i=1;i<10;i+=2) s+=i+1; printf("%dn",s);
A.自然数1~9的累加和
B.自然数1~10的累加和
C.自然数1~9中的奇数之和
D.自然数1~10中的偶数之和
1+2+……+11 -
第4题:
77个连续自然数的和是7546,则其中第45个自然数是( )。
A.91
B.100
C.104
D. 105
正确答案:C
[(2a1+76)×77]/2=7546
a1=60∴a45=60+44=104。
故本题正确答案为C。 -
第5题:
77个连续自然数的和是7546,则其中第45个自然数是()。
. 91 B. 100 C. 104 D. 105答案:C解析:[(2a1+76)×77]/2=7546。a1=60∴a45=60+44=104。故答案为C。
