100以内的正整数中，同时能被3和4整除的数有几个?（ ）A．4个B．8个C．16个D．24个

题目

100以内的正整数中，同时能被3和4整除的数有几个?（ ）

A．4个

B．8个

C．16个

D．24个

相似考题

1.在全部为全速率话音信道情况下，每个载频的话音信道数为()。A.4个B.8个C.16个

2.在帧中继的帧结构中，地址字段最小占( )A．4比特B．8比特C．16比特D．24比特

3.Pentium微处理器的每个突发式总线周期传送多少数据？A．4个字节B．8个字节C．16个字节D．32个字节

4.BSC协议中的控制行DEL占( )A．1个比特B．8个比特C．16个比特D．24个比特

更多“100以内的正整数中,同时能被3和4整除的数有几个?( ) A.4个B.8个C.16个D.24个 ”相关问题

  • 第1题：

    羔羊的饲养月龄一般平均为______。

    A.4～8个月龄

    B.8～12个月龄

    C.12～24个月龄

    D.24～32个月龄


    参考答案：B

  • 第2题：

    从1，2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为（ ）。

    A．134

    B．267

    C．316

    D．133


    正确答案：A
    取出的N个不同的数，任意三个的和都能被15整除，分两种情况：
    (1)这N个数都能被15整除
    在1—2007中，能被15整除的数为15×1，15×2，…，15×133，共有133个。
    (2)这N个数除以15的余数都为5
    在1—2007中，能被15除余5的数为15×0＋5，15×1＋5，…，15×133＋5，共有134个。故N最大为134。

  • 第3题：

    Penfium微处理器的每个突发式总线周期传送( )数据。

    A．4个字节

    B．8个字节

    C．16个字节

    D．32个字节


    正确答案：D

  • 第4题：

    n为 100 以内的自然数，那么能令2n-1被7 整除的n有多少个？

    A.32

    B.33

    C.34

    D.35


    正确答案：B
    7.B.［解析］ 当 n 是3 的倍数的时候，2n-1是 7 的倍数。也就是求 100 以内3 的倍数，从 3到 99，共有33 个。故选 B。

  • 第5题：

    使用两个8259A进行级联，最大可以获得的有效硬件中断源的个数为( )。

    A．4个

    B．8个

    C．16个

    D．15个


    正确答案：D
    解析：使用两个8259A进行级联，最大可以获得的有效硬件中断源的个数为15个(其中有一个引脚用做级联了)。

  • 第6题：

    1、2、3、4、5、8这七个数字能够组成多少个能被125整除且无重复数字的五位数? A．9 B．12 C．21 D．24


    正确答案：C
    能被125整除，则符合题意的五位数的后三位应该是125或者250。如果后三位数是125，则有3x3=9个数；如果后三位数是250，则有4x3=12个数。故一共可以组成9+12=21个能被125整除的五位数。

  • 第7题：

    对于16×16的BANYAN网络,每一级需要的交换单元为()。

    A.4个

    B.8个

    C.16个

    D.32个


    参考答案：B

  • 第8题：

    n为100以内的自然数，那么能令2n +1被7整除的n有多少个？

    A.32
    B. 33
    C.34
    D.35

    答案：B
    解析：
    .［解析］ 当n是3的倍数的时候， 是7的倍数。也就是求100以内3的倍数，从3到99，共有33个。故选B。

  • 第9题：

    从1，2，3，……，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除。问最多可取几个数？（）

    A.14个
    B.15个
    C.16个
    D.17个

    答案：C
    解析：
    任意两个数之积不能被4整除，即两个数分别不能被4整除,那么所取数中最多只能有一个偶数，且该偶数不能为4的倍数;共有15个奇数，所以最多可以取15+1=16个数。故正确答案为C。

  • 第10题：

    n为100以内的自然数，那么能令2的n次方-1被7整除的n有多少个？



    A.32
    B.33
    C.34
    D.35

    答案：C
    解析：
    .［解析］ 当n是3的倍数的时候，2的n次方-1是7的倍数。也就是求100以内3的倍数，从0到99，共有34个。故选C。

  • 第11题：

    充分条件指的是对于两个命题X和Y，当X成立时，则Y成立，那么X是Y的充分条件；必要要条件指的是对于两个命题X和Y，当X不成立时，则Y不成立，那么X是Y的必要条件。
    根据上述定义，下列哪项中X是Y的必要条件？

    A.X：该数能被6整除；Y：该数能被2整除
    B.X：该数能被6整除；Y：该数能被4整除
    C.X：该数能被3整除；Y：该数能被6整除
    D.X：该数能被4整除；Y：该数能被3整除

    答案：C
    解析：
    本题考查“必要条件”的定义。
    其关键信息为：当X不成立时，则Y不成立。
    A项，当一个数不能被6整除时，无法得到该数不能被2整除，比如“4”，不符合定义，故A项错误，排除。
    B项，当一个数不能被6整除时，无法得到该数不能被4整除，比如“4”，不符合定义，故B项错误，排除。
    C项，因为6可以被分解为2×3，所以不能被3整除，就一定就不能被6整除，符合定义，故C项正确，当选。
    D项，当一个数不能被4整除时，无法得到该数不能被3整除，比如“6”，不符合定义，故D项错误，排除。
    故本题的正确答案为C项。

  • 第12题：

    单选题
    在1，2，3，…，40中，至少要取出几个数，才能保证取出的数中一定有一个数能被4整除？（）
    A

    3

    B

    4

    C

    21

    D

    31


    正确答案： D
    解析： 1，2，3，…，40中，能被4整除的有10个，因此最少要取出40-10+1=31个才能满足题干要求，选D。

  • 第13题：

    应急小车上PTP58500的无线以太网桥可提供()个E1电路。

    A.4个

    B.8个

    C.16个


    参考答案：A

  • 第14题：

    在1至100这100个数中，有既不能被5整除也不能被9整除的数，它们的和是( )。

    A 1 644

    B．1779

    C．3406

    D．3541


    正确答案：D
    64．D[解析]先求出被5或9整除的数的和。
    1至100中被5整除的数有5，10，15，?，100，和为：5+10+15+?+100=(100+5)X 20÷2=1050
    1至100中被9整除的数有9，18，?，99，和为：9+18+27+?+99=(9+99)×ll÷2=594
    又因为1— 100中， 45、90这两个数同时被5与9整除， 于是所求的和是(1+2+?+
    100)一(5+10+?+100)一(9+18+?+99)+(45+90)=3541。
    因此，本题正确答案为D。

  • 第15题：

    在410，108，870和315四个数中，能同时被2、3、5整除的数是（ ）。

    A．410

    B．108

    C．870

    D．315


    正确答案：C
    同时被2，3，5整除的数是870，即870÷30=29。

  • 第16题：

    HDLC的帧格式中，帧校验序列字段占( )

    A．1个比特

    B．8个比特

    C．16个比特

    D．24个比特


    正确答案：C

  • 第17题：

    从1.2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为()。

    A．134

    B．267

    C．316

    D．133


    正确答案：A

  • 第18题：

    在1至100的自然数中，不能被2整除且不能被3整除且不能被5整除的数共有多少个?（ ） A．23个 B．26个 C．27个 D．74个


    正确答案：B

    1至100的自然数中，能被2整除的数有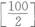=50个，能被3整除的数有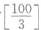=33个，能被5整除的数有=20个，能被2整除且能被3整除的数有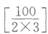＝16个，能被5整除且能被3整除的数有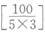＝6个，能被2整除且能被5整除的数有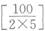＝10个，能被2整除且能被3整除且能被5整除的数有=3个，故由容斥原理，不能被2整除且不能被3整除且不能被5整除的数共有100－[50+33+20－(16+6+10)+3]=26个。故选B。

  • 第19题：

    RBS200里每块RTT板能带多少个TRX?()

    A.4个

    B.8个

    C.16个

    D.2个


    参考答案：A

  • 第20题：

    1～200这200个自然数中，能被4或能被6整除的数有多少个？( )


    A. 65
    B. 66
    C. 67
    D. 68

    答案：C
    解析：
    能被4整除的有[200/4]＝50个能被6整除的有[200/6]＝33个注：[]表示取整而两者却重复计算了同时能被4和6整除的数，所以需要减去能被4，6共同整除的有[200/12]＝16个于是能被4或能被6整除的数50+33-16＝67个

  • 第21题：

    从1、2、3、4、5中随机抽取3个数，问这3个数之和至少能被其中一个数整除的概率是多少？

    A. 10%
    B. 30%
    C. 60%
    D. 90%

    答案：D
    解析：
    三个数中只要含有1就能满足，共C4,2=6种，三个数中含有2的话，三个数的和必须是偶数，共C3,2-1=2种，不含1和2只有3、4、5能被3整除，因此共有9种满足的情况，总数为c5,3=10，概率为9/10=90%。

  • 第22题：

    如果用一个圆来表示词语所指称的对象的集合，那么以下哪项中三个词语之间的关系符合下图？

    A.①能被23整除的正整数，②6的因子，③10以内的正整数
    B.①20的因子，②40以内的正整数，③能被43整除的正整数
    C.①50以内的正整数，②能被41整除的正整数，③49的因子
    D.①100以内的正整数，②87的因子，③能被73整除的正整数

    答案：A
    解析：
    本题属于外延关系题目。
    根据图示确定①、②、③这三者之间的关系：①与②、③是全异关系，③包含②。
    辨析选项：
    A项，①能被23整除的正整数，例如：23、46、69……，②6的因子是1、2、3、6（因子就是所有可以整除这个数的数），所以①和②是全异关系，③10以内的正整数包括②，与题干图示的关系一致，符合；
    B项，①20的因子1、2、4、5、10、20，与②40以内的正整数是包含关系，与题干图示的关系不一致，排除；
    C项，①50以内的正整数和②能被41整除的正整数（41、82…..）是交叉关系，与题干图示逻辑关系不一致，排除；
    D项，①100以内的正整数和②87的因子是交叉关系，与题干图示逻辑关系不一致，排除。
    因此，选择A选项。

  • 第23题：

    编写一个Java程序，对于给定的年份，回答“Leap Year”（闰年）或者“Not a Leap Year”（平年）。如果一个年份能被4整除，但是不能被100整除，它是闰年；如果一个年份能被100整除，也能被400整除，它也是闰年。需要定义名为LeapYear的服务提供类

    略

相关内容