有5个不同的自然数，它们当中任意3个的和是3的倍数，任意4个的和是4的倍数，那么满足以上条件的5个数的和最小是（ ）。A．96B．108C．116D．125

题目

有5个不同的自然数，它们当中任意3个的和是3的倍数，任意4个的和是4的倍数，那么满足以上条件的5个数的和最小是（ ）。

A．96

B．108

C．116

D．125

相似考题

1.一个小于60的自然数与3的和是5的倍数，与3的差是6的倍数，这个数最大是多少?（ ）A．47B．51C．52D．57

2.任意5个整数中,其中有3个整数的和为3的倍数。()此题为判断题(对，错)。

3.关于任意5个不相同的自然数,下列哪个叙述是正确的?()A、其中最少有两个数的差是4的倍数B、其中最少有两个数的差是5的倍数C、其中最少有两个数的差是6的倍数D、其中最少有两个数的差是7的倍数

4.如果a=3b(a、b都是不为0的自然数)，那么a和b的最大公约数是（ ），最小公倍数是 （ ）。

更多“有5个不同的自然数,它们当中任意3个的和是3的倍数,任意4个的和是4的倍数,那么满足以上 ”相关问题

  • 第1题：

    有四个不同的正整数，其中任意两个数之和是2的倍数，任意三个数的和是3的倍数，满足条件的最小的四个正整数之和是：

    A．51

    B．38

    C．40

    D．42


    正确答案：C
    首先这4个数必须同奇偶，其次这4个数必须对于3同余则4个数必须对6同余；又要最小则4个数中最小的是1，所以1、7、13、19是满足条件的最小的四个正整数，和为40。

  • 第2题：

    有4个不同的自然数，它们当中任意两数的和是2的倍数；任意3个数的和是3的倍数，为了使得这4个数的和尽可能小，则这四个数的和为（ ）。

    A. 40
    B. 42
    C. 46
    D. 51

    答案：A
    解析：
    任意两个数的和是2的倍数，所以这些数的奇偶性相同。任意三个数的和是3的倍数，所以这些数除以3，所得余数必定相同（否则在三个数的和中换一个数，和将不是3的倍数）。于是， 这些数除以6所得余数相同，故这最小的四个数为1，7，13，19。所以这四个数的和为1 + 7 + 13 + 19 = 40。

  • 第3题：

    有4个不同的自然数，它们当中任意两数的和是2的倍数；任意3个数的和是3的倍数，为了使得这4个数的和尽可能小，则这四个数的和为（　　）。
    A.40
    B.42
    C.46
    D.51


    答案：A
    解析：
    任意两个数的和是2的倍数，所以这些数的奇偶性相同；任意三个数的和是3的倍数，所以这些数除以3，所得余数必定相同(否则在三个数的和中换一个数，和将不是3的倍数)。于是这些数除以6所得余数相同，故这最小的四个数为1、7、13、19。所以这四个数的和为1+7+13+19=40。

  • 第4题：

    从任意的自然数中，至少选取（）个数，才能保证一定有两个数的差是5的倍数？

    • A、2
    • B、6
    • C、8
    • D、12

    正确答案:B

  • 第5题：

    单选题
    如果a和b都是非零自然数，且a＝8b，那么a和b的最小公倍数是（）。
    A

    1

    B

    a

    C

    b


    正确答案： A
    解析： 暂无解析

  • 第6题：

    单选题
    有4个不同的自然数，他们当中任意两数的和是2的倍数，任意3个数的和是3的倍数，为了使这4个数的和尽可能小，则这4个数的和为（）
    A

    40

    B

    42

    C

    46

    D

    51


    正确答案： D
    解析： 暂无解析

  • 第7题：

    在1,2,3…100这100个自然数中，取两个不同的数，使得它们的和是7的倍数，共有 ( )种不同的取法。

    A．700

    B．707

    C．697

    D．705


    正确答案：B
    [答案] B。解析：100÷7=14……2。在1～100中，按被7除的余数分为了类：余1与余2的各15个，余3、余4、余5、余6、整除的各14个。取两个不同的数，要使它们的和是7的倍数，必须是：一个余1一个余6，或一个余2一个余5，或一个余3一个余4，或两个都是整除。所以，不同的取法共有15×14+15×14+14×14+14×13÷2=707。

  • 第8题：

    盒中有8个球，上面分别写着2，3，4，5，7，8，10，12八个数，甲乙两人玩摸球游戏，下面规则中对双方都公平的是()。

    A.任意摸一球，是质数甲胜，是合数乙胜
    B.任意摸一球，是2的倍数甲胜，是3的倍数乙胜
    C.任意摸一球，小于5甲胜，大于5乙胜’
    D.任意摸一球，是奇数甲胜，是偶数乙胜

    答案：A
    解析：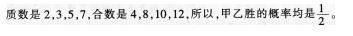

  • 第9题：

    某自然数a是3的倍数，a-1是4的倍数，a-2是5的倍数，则a最小为（__）？

    A. 57
    B. 37
    C. 117
    D. 27

    答案：A
    解析：
    本题考查余数同余问题。代入验证，57,117符合题意，但是要找的是最小的，应选择57

  • 第10题：

    如果a和b都是非零自然数，且a＝8b，那么a和b的最小公倍数是（）。

    • A、1
    • B、a
    • C、b

    正确答案:B

  • 第11题：

    单选题
    有两个自然数，它们的和等于297，它们的最大公约数与最小公倍数之和等于693。这两个自然数的差等于多少？（　　）
    A

    33

    B

    27

    C

    11

    D

    9


    正确答案： C
    解析：
    设这两个数是AM、BM，M是这两个数的最大公约数，其中A、B、M均为整数。AM＋BM＝（A＋B）×M＝297，M＋A×B×M＝（1＋A×B）×M＝693，所以M是297和693的公约数。297和693的最大公约数为99。99＝32×11，把M＝1，3，9，11，33，99分别代入两个式子试算。①（A＋B）×1＝297，（1＋A×B）×1＝693，无解；②（A＋B）×3＝297，（1＋A×B）×3＝693，无解；③（A＋B）×9＝297，（1＋A×B）×9＝693，无解；④（A＋B）×11＝297，（1＋A×B）×11＝693，无解；⑤（A＋B）×33＝297，（1＋A×B）×33＝693，此时A、B一个是4，一个是5；⑥（A＋B）×99＝297，（1＋A×B）×99＝693，无解。所以⑤符合题意，当M＝33时，一个数是4×33＝132，一个数是5×33＝165，即这两个自然数的差为165－132＝33。

  • 第12题：

    单选题
    脉冲转换增压适用的最佳缸数是（）。
    A

    三的整倍数

    B

    四的整倍数

    C

    五的整倍数

    D

    任意缸数


    正确答案： C
    解析： 暂无解析

相关内容