【问题2】(7分)考虑表4-1的实例,假设有3个物品,背包容量为22。图4-1中是根据上述算法构造的搜索树,其中结点的编号表示了搜索树生成的顺序,边上的数字1/0分别表示选择/不选择对应物品。除了根结点之外,每个左孩子结点旁边的上下两个数字分别表示当前背包的重量和已获得的价值,右孩子结点旁边的数字表示扩展了该结点后最多可能获得的价值。为获得最优解,应该选择物品 (5) ,获得的价值为 (6) 。对于表4-1的实例,若采用穷举法搜索整个解空间,则搜索树的结点数为 (7) ,而用了上述回溯法,搜索树的结点数为
题目
【问题2】(7分)
考虑表4-1的实例,假设有3个物品,背包容量为22。图4-1中是根据上述算法构造的搜索树,其中结点的编号表示了搜索树生成的顺序,边上的数字1/0分别表示选择/不选择对应物品。除了根结点之外,每个左孩子结点旁边的上下两个数字分别表示当前背包的重量和已获得的价值,右孩子结点旁边的数字表示扩展了该结点后最多可能获得的价值。为获得最优解,应该选择物品 (5) ,获得的价值为 (6) 。

对于表4-1的实例,若采用穷举法搜索整个解空间,则搜索树的结点数为 (7) ,而用了上述回溯法,搜索树的结点数为 (8) 。
相似考题
更多“ 【问题2】(7分)考虑表4-1的实例,假设有3个物品,背包容量为22。图4-1中是根据上述算法构造的搜索树,其中结点的编号表示了搜索树生成的顺序,边上的数字1/0分别表示选择/不选择对应物品。除了根结点之外,每个”相关问题
-
第1题:
最优二叉树(哈夫曼树)、最优查找树均为平均查找路径长度Σwl最小的树,其中对于最优二叉树,n表示(42);对于最优查找树,n表示(43);构造这两种树均(44)。
A.结点数
B.叶结点数
C.非叶结点数
D.度为二的结点数
正确答案:B
-
第2题:
阅读以下说明和C函数,将应填入(n)处的字句写在对应栏内。
【说明】
已知某二叉树的非叶子结点都有两个孩子结点,现将该二叉树存储在结构数组Ht中。结点结构及数组Ht的定义如下:
define MAXLEAFNUM 30
struct node{
char ch; /*当前结点表示的字符,对于非叶子结点,此域不用*/
char *pstr; /*当前结点的编码指针,非叶子结点不用*/
int parent; /*当前结点的父结点,为0时表示无父结点*/
int lchild,rchild;
/*当前结点的左、右孩子结点,为0时表示无对应的孩子结点*/
};
struct node Ht[2*MAXLEAFNUM]; /*数组元素Ht[0]不用*/
该二叉树的n个叶子结点存储在下标为1~n的Ht数组元素中。例如,某二叉树如果其存储结构如下图所示,其中,与叶子结点a对应的数组元素下标为1,a的父结点存储在Ht[5],表示为Ht[1].parent=5。Ht[7].parent=0表示7号结点是树根,Ht[7].child=3、Ht[7].rchild=6分别表示7号结点的左孩子是3号结点、右孩子是6号结点。

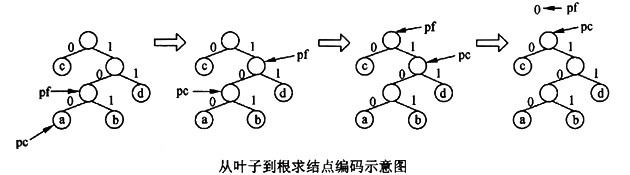
如果用0或1分别标识二叉树的左分支和右分支(如上图所示),从根结点开始到叶子结点为止,按所经过分支的次序将相应标识依次排列,可得到一个0、1序列,称之为对应叶子结点的编码。例如,上图中a,b,c,d的编码分别是100,101,0,11。
函数LeafCode(Ht[],n)的功能是:求解存储在Ht中的二叉树中所有叶子结点(n个)的编码,叶子结点存储在Ht[1]~Ht[n]中,求出的编码存储区由对应的数组元素pstr域指示。
函数LeafCode从叶子到根逆向求叶子结点的编码。例如,对上图中叶子结点a求编码的过程如下图所示。
typedef enum Status {ERROR,OK} Status;
【C函数】
Status LeafCode(struct node Ht[], int n)
{
int pc, pf; /*pc用于指出树中的结点,pf则指出pc所对应结点的父结点*/
int i,start;
char tstr[31] = {'\0'}; /*临时存储给定叶子结点的编码,从高下标开始存入*/
for(i = 1;(1); i++){ /*对所有叶子结点求编码,i表示叶结点在HT数组中的下标*/
start = 29;
pc = i; pf = Ht[i].parent;
while (pf !=(2)) { /*没有到达树根时,继续求编码*/
if ((3).lchild == pc ) /*pc所表示的结点是其父结点的左孩子*/
tstr[--start] = '0';
else
tstr[--start] = '1';
pc =(4); pf = Ht[pf].parent; /*pc和pf分别向根方向回退一层*/
}/* end of while */
Ht[i].pstr = (char *) malloc(31-start);
if (!Ht[i].pstr) return ERROR;
strcpy(Ht[i].pstr,(5));
}/* end of for */
return OK;
}/* and of LeafCode */
正确答案:(1) i=n或其等价表示 (2) 0 (3) Ht[pf]或(*(Ht+pf)) (4) pf (5) &tstr[start]或tstr+start
(1) i=n,或其等价表示 (2) 0 (3) Ht[pf],或(*(Ht+pf)) (4) pf (5) &tstr[start],或tstr+start 解析:本题考查C语言的基本控制结构、数组以及参数传递基础知识。
哈夫曼算法构造最优二叉树的过程如下。
(1)根据给定的n个权值{W1,W2,…,Wn}构成n棵二叉树的集合F={T1,T2,…, Tn},其中每棵二叉树Ti中只有一个带权为Wi的根结点,其左、右子树均空。
(2)在F中选取两棵根结点权值最小的树作为左、右子树构造一棵新的二叉树,且置新二叉树的根结点的权值为其左、右子树根结点的权值之和。
(3)在F中删除这两棵二叉树,同时将新得到的二叉树加入F中。
(4)重复(2)和(3),直到F只含一棵树为止。这棵树便是最优二叉树。
最优二叉树是从叶子到根构造起来的,每次都是先确定一棵二叉树的左、右子树,然后再构造出树根结点,因此,最优二叉树中只有叶子结点和分支数为2的内部结点。若已知叶子的数目为n,则内部结点数比叶子少1,因此,整棵树所需的存储空间规模是确定的,可以采用数组空间来存储最优二叉树。
题目中已经指出该二叉树的n个叶子结点存储在下标为1~n的Ht数组元素中,同时举例说明父结点编号为0的结点式树根结点。因此,空(1)处应填入“i=n”。同时,除了根结点之外,每个结点都有唯一的父结点,因此到达树根的标志为结点的父结点编号为0,因此,空(2)处应填入“0”。
根据代码中pc和pf的作用:pc用于指出树中的结点,pf则指出pc所对应结点的父结点,则空(3)处应填入“Ht[pf]”,空(4)处填入“pf”使得pc回退至其父结点位置。
空(5)考查了标准函数的调用,对于函数strcpy(),其原型为char* strcpy (char*,const char*)。两个参数都是字符指针,根据代码中tstr的作用,应将tstr+start(tstr[start]~tstr[29]存放编码)作为实参调用strcpy,因此空(5)处应填入“tstr+start”或“&tstr[start]”。 -
第3题:
对二叉树中的结点如下编号:树根结点编号为1,根的左孩子结点编号为2、右孩子结点编号为3,依此类推,对于编号为i的结点,其左孩子编号为2i、右孩子编号为2i+1。例如,下图所示二叉树中有6个结点,结点a、b、c、d、e、f的编号分别为1、2、3、5、7、11。那么,当结点数为n(n>0)的( )时,其最后一个结点编号为2i-1

A.二叉树为满二叉树(即每层的结点数达到最大值)B.二叉树中每个内部结点都有两个孩子C.二叉树中每个内部结点都只有左孩子D.二叉树中每个内部结点都只有右孩子
正确答案:C
-
第4题:
考虑一个背包问题,共有n=5个物品,背包容量为W=10,物品的重量和价值分别为:w={2,2,6,5,4},v={6,3,5,4,6},求背包问题的最大装包价值。若此为0-1背包问题,分析该问题具有最优子结构,定义递归式为

其中c(i,j)表示i个物品、容量为j的0-1背包问题的最大装包价值,最终要求解c(n,W)。 采用自底向上的动态规划方法求解,得到最大装包价值为(62),算法的时间复杂度为(63)。 若此为部分背包问题,首先采用归并排序算法,根据物品的单位重量价值从大到小排序,然后依次将物品放入背包直至所有物品放入背包中或者背包再无容量,则得到的最大装包价值为(64),算法的时间复杂度为(65)。
A.11
B.14
C.15
D.16.67
正确答案:C
-
第5题:
最佳二叉搜索树是______。
A.关键码个数最少的二叉搜索树
B.搜索时平均比较次数最少的二叉搜索树
C.所有结点的左子树都为空的二叉搜索树
D.所有结点的右子树都为空的二叉搜索树
正确答案:B
解析:最佳二叉搜索树是搜索时平均比较次数最少的二叉搜索树。 -
第6题:
根据权值集合{0.30,0.25,0.25,0.12,0.08}构造的哈夫曼树中,每个权值对应哈夫曼树中的一个叶结点()A.根结点到所有叶结点的路径长度相同
B.根结点到权值0.30和0.25所表示的叶结点路径长度相同
C.根结点到权值0.30所表示的叶结点路径最长
D.根结点到权值0.25所表示的两个叶结点路径长度不同答案:B解析:根据哈夫曼树构造原则,画出哈夫曼树如下: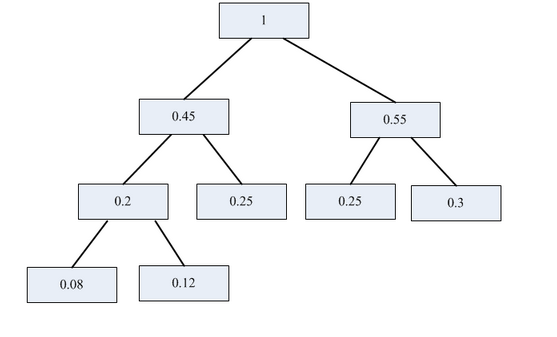
-
第7题:
对下图所示的二叉树进行顺序存储(根结点编号为1,对于编号为i的结点,其左孩子结点为2i,右孩子结点为2i+1)并用一维数组BT来表示,已知结点X、E和D在数组BT中的下标分别为1、2、3,可推出结点G、K和H在数组BT中的下分别为( )。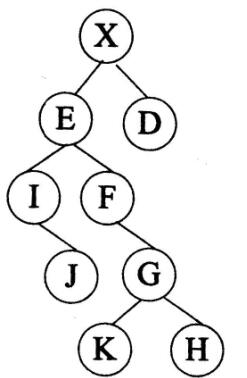 A.10、11、12
A.10、11、12
B.12、24、25
C.11、12、13
D.11、22、23答案:D解析:元素G为F的右子树,其下标为2F+1 ; F为元素E的右子树,其下标为2E+1, E的下标为2,因此G=2* (2*2+1) +1=11 ; K=2G=22 ; H=2G+1=23 ; -
第8题:
设有序表为(13,19,25,36,48,51,63,84,91,116,135,200),元素的下标依次为1,2,……,12。画出对上述有序表进行折半查找所对应的判定树(树结点用下标表示)。

略 -
第9题:
有0-1背包问题如下: n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大。 P=(15,8,6,4,3,1),W=(2,3,4,5,8,10),单位重量物品价值(7.5,2.67,1.5,0.8,0.375,0.1)
正确答案: 可知随着物品的重量增加,物品的价值减少;因此可以用贪心算法来求解。以选取单位重量物品价值高为贪心策略。
1.先把重量为2的物品放进背包,此时剩余载重量为17,P为15。
2.把重量为3的物品放进背包,此时剩余载重量为14,P为23;
3.把重量为4的物品放进背包,此时剩余载重量为10,P为29;
4.把重量为5的物品放进背包,此时剩余载重量为5,P为33;
由于8>5,所以不能再放进背包。
结果是把重量为2,3,4,5的物品装进背包,总价值最大为33。 -
第10题:
假定一棵二叉树顺序存储在一维数组a中,但让编号为1的结点存入a[0]元素中,让编号为2的结点存入a[1]元素中,其余类推,则编号为i结点的左孩子结点对应的存储位置为(),若编号为i结点的存储位置用j表示,则其左孩子结点对应的存储位置为()。
正确答案:2i-1;2j+1 -
第11题:
填空题假定一棵二叉树顺序存储在一维数组a中,但让编号为1的结点存入a[0]元素中,让编号为2的结点存入a[1]元素中,其余类推,则编号为i结点的左孩子结点对应的存储位置为(),若编号为i结点的存储位置用j表示,则其左孩子结点对应的存储位置为()。正确答案: 2i-1,2j+1解析: 暂无解析 -
第12题:
单选题下面关于哈夫曼树的说法,不正确的是()A对应于一组权值构造出的哈夫曼树一般不是唯一的
B哈夫曼树具有最小带权路径长度
C哈夫曼树中没有度为1的结点
D哈夫曼树中除了度为1的结点外,还有度为2的结点和叶结点
正确答案: D解析: 暂无解析 -
第13题:
阅读下列说明,回答问题1至问题2,将解答填入答题纸的对应栏内。
【说明】
0—1背包问题可以描述为:有n个物品,对i=l,2,…,n,第i个物品价值为vi,重量为wi(vi和wi为非负数),背包容量为w(W为非负数),选择其中一些物品装入背包,使装入背包物品的总价值最大,即
 ,且总重量不超过背包容量,即
,且总重量不超过背包容量,即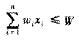 ,其中,xi∈{O,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品放入背包。
,其中,xi∈{O,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品放入背包。用回溯法求解此0—1背包问题,请填充下面伪代码中(1)~(4)处空缺。
回溯法是一种系统的搜索方法。在确定解空间后,回溯法从根结点开始,按照深度优先策略遍历解空间树,搜索满足约束条件的解。对每一个当前结点,若扩展该结点已经不满足约束条件,则不再继续扩展。为了进一步提高算法的搜索效率,往往需要设计一个限界函数,判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOuND(v,w,k,W)函数,其中v、w、k和w分别表示当前已经获得的价值、当前背包的重量、已经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点,该函数值表示确定了部分物品是否选择之后,对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值,若该价值小于等于当前已经得到的最优解,则该结点无需再扩展。下面给出0—1背包问题的回溯算法伪代码。
函数参数说明如下:w:背包容量;n:物品个数;w:重量数组;v:价值数组;fw:获得最大价值时背包的重量;fp:背包获得的最大价值;X:问题的最优解。
变量说明如下:
cw:当前的背包重量;cp:当前获得的价值;k:当前考虑的物品编号;Y:当前已获得的部分解。
BKNAP(W,n,w,v,fw,fp,X)
1 cw←cp0
2 (1)
3 fp←l
4 while true
5 while k≤n and cw+w[k]≤w d。
6 (2)
7 cp←cp+v[k]
8 Y[k]←l
9 k←k+1
10 if k>n then
11 if fp<cp then
12 fp←cp
13 fw←cw
14 k←n
15 X←Y
16 else Y (k)←O
17 while BOUND(cp,cw,k,W) ≤fp do
18 while k≠O and Y(k)≠l d0
19 (3)
20 if k=0 then return
2l Y[k]←0
22 cw←cw-w[k]
23 cp←cp-v[k]
24 (4)
正确答案:(1)k←1(2)cw←cw+w[k](3)k←k-1(4)k←k+l
(1)k←1(2)cw←cw+w[k](3)k←k-1(4)k←k+l -
第14题:
0-1背包问题可以描述为:有n个物品,对i=1,2,…,n,第i个物品价值为vi ,重量为wi(vi,和wi为非负数),背包容量为W(W为非负数),选择其中一些物品装入背包,使装入背包物品的总价值最大,
 ,且总重量不超过背包容量,即
,且总重量不超过背包容量,即 ,其中,xi∈{0,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品 放入背包。
,其中,xi∈{0,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品 放入背包。【问题1】(8分)
用回溯法求解此0-1背包问题,请填充下面伪代码中(1)~(4)处空缺。
回溯法是一种系统的搜索方法。在确定解空间后,回溯法从根结点开始,按照深度优先策略遍历解空间树,搜索满足约束条件的解。对每一个当前结点,若扩展该结点己经不满足约束条件,则不再继续扩展。为了进一步提高算法的搜索效率,往往需要设计一个限界函数,判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOUND(v,w,k,W)函数,其中v, w, k和W分别表示当前已经获得的价值、当前背包的重量、己经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点,该函数值表示确定了部分物品是否选择之后,对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值,若该价值小于等于当前已经得到的最优解,则该结点无需再扩展。
下面给出0-1背包问题的回溯算法伪代码。
函数参数说明如下:
W:背包容量;n:物品个数;w:重量数组;v:价值数组;fw:获得最大价值时背包的重量;fp:背包获得的最大价值;X:问题的最优解。
变量说明如下:
cw:当前的背包重量;cp:当前获得的价值;k:当前考虑的物品编号;Y:当前已获得的部分解。
BKNAP(W,n,w,v,fw,fp,X)
1 cw ← cp ← 0
2 (1)
3 fp ← -1
4 while true
5 while k≤n and cw+w[k]≤W do
6 (2)
7 cp ← cp+v[k]
8 Y[k]← 1
9 k ← k+1
10 if k>n then
11 if fp<cp then
12 fp ← cp
13 fw ← ew
14 k ← n
15 X ← Y
16 else Y(k)← 0
17 while BOUND(cp,cw,k,W) ≤fp do
18 while k≠0 and Y(k)≠1 do
19 (3)
20 if k=0 then return
21 Y[k]←0
22 cw ← cw ← w[k]
23 cp ← cp ← v[k]
24 (4)
正确答案:本题考查的是用回溯法求解0-1背包问题。回溯法有两类算法框架:非递归形式和递归形式,本题采用非递归形式表示。理解回溯法的基本思想和这两类算法框架是正确解答本题的根本要求·回溯法从第一项物品开始考虑是否应该装入背包中,因此当前考虑的物品编号k从1开始,即k←1。然后逐项往后检查,若能全部放入背包则将该项放入背包,此时背包的重量应该是当前的重量加上当前考虑物品的重量,即cw←cw+w[k],当然背包中物品的价值也为当前的价值加上当前考虑物品的价值。若己经考虑完了所有的物品,则得到一个解,判断该解是否为当前最优,若为最优,则将该解的信息放入变量fp、fw和X中。若还没有考虑完所有的物品,意味着有些物品不能放入背包,此时先判断若不将当前的物品放入背包中,则其余物品放入背包是否可能得到比当前最优解更优的解,若得不到则回溯;否则继续考虑其余的物品。
【问题1】(共8分,各2分)
(1)k ← 1 或其等价形式
(2)cw ← cw + w[k] 或其等价形式
(3)k ← k – 1 或其等价形式
(4)k ← k + l 或其等价形式
-
第15题:
阅读以下说明和C代码,填补代码中的空缺,将解答填入答题纸的对应栏内。 【说明】 二叉查找树又称为二叉排序树,它或者是一棵空树,或者是具有如下性质的二叉树。 (1)若它的左子树非空,则左子树上所有结点的值均小于根结点的值。 (2)若它的右子树非空,则右子树上所有结点的值均大于根结点的值。 (3)左、右子树本身就是两棵二叉查找树。 二叉查找树是通过依次输入数据元素并把它们插入到二叉树的适当位置上构造起来的,具体的过程是:每读入一个元素,建立一个新结点,若二叉查找树非空,则将新结点的值与根结点的值相比较,如果小于根结点的值,则插入到左子树中,否则插入到右子树中;若二叉查找树为空,则新结点作为二叉查找树的根结点。 根据关键码序列{46,25,54,13,29,91}构造一个二叉查找树的过程如图4-1所示。
 设二叉查找树采用二叉链表存储,结点类型定义如下: typedef int KeyType; typedef struct BSTNode{ KeyType key; struct BSTNode *left,*right; }BSTNode,*BSTree; 图4-1(g)所示二叉查找树的二叉链表表示如图4-2所示。
设二叉查找树采用二叉链表存储,结点类型定义如下: typedef int KeyType; typedef struct BSTNode{ KeyType key; struct BSTNode *left,*right; }BSTNode,*BSTree; 图4-1(g)所示二叉查找树的二叉链表表示如图4-2所示。 图4-2 函数int InsertBST(BSTree *rootptr,KeyType kword)功能是将关键码kword插入到由rootptr指示出根结点的二叉查找树中,若插入成功,函数返回1,否则返回0。
图4-2 函数int InsertBST(BSTree *rootptr,KeyType kword)功能是将关键码kword插入到由rootptr指示出根结点的二叉查找树中,若插入成功,函数返回1,否则返回0。【C代码】 int lnsertBST(BSTree*rootptr,KeyType kword) /*在二叉查找树中插入一个键值为kword的结点,若插入成功返回1,否则返回0; *rootptr为二叉查找树根结点的指针 */ { BSTree p,father; (1) ; /*将father初始化为空指针*/ p=*rootptr; /*p指示二叉查找树的根节点*/ while(p&& (2) ){ /*在二叉查找树中查找键值kword的结点*/ father=p; if(kword<p->key) p=p->left; else p=p->right; } if( (3) )return 0; /*二叉查找树中已包含键值kword,插入失败*/ p=(BSTree)malloc( (4) ); /*创建新结点用来保存键值kword*/ If(!p)return 0; /*创建新结点失败*/ p->key=kword; p->left=NULL; p->right=NULL; If(!father) (5) =p; /*二叉查找树为空树时新结点作为树根插入*/ else if(kword<father->key) (6) ; /*作为左孩子结点插入*/ else (7) ; /*作右孩子结点插入*/ return 1; }/*InsertBST*/
正确答案:father=(void*)0
keyword!=p->key
p
sizeof(BSTNode)
*rootptr
father->left=p
father->right=p
-
第16题:
【问题 1】(8 分)
用回溯法求解此 0-1 背包问题,请填充下面伪代码中(1)~(4)处空缺。
回溯法是一种系统的搜索方法。在确定解空间后,回溯法从根结点开始,按照深度优先策略遍历解空间树,搜索满足约束条件的解。对每一个当前结点,若扩展该结点已经不满足约束条件,则不再继续扩展。为了进一步提高算法的搜索效率,往往需要设计一个限界函数,判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOUND( v,w,k,W )函数,其中 v、w、k 和 W分别表示当前已经获得的价值、当前背包的重量、已经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点,该函数值表示确定了部分物品是否选择之后,对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值,若该价值小于等于当前已经得到的最优解,则该结点无需再扩展。
下面给出 0-1背包问题的回溯算法伪代码。
函数参数说明如下:
W:背包容量;n:物品个数;w:重量数组;v:价值数组;fw:获得最大价值时背包的重量;fp:背包获得的最大价值;X:问题的最优解。
变量说明如下:
cw:当前的背包重量;cp:当前获得的价值;k:当前考虑的物品编号;Y:当前已获得的部分解。
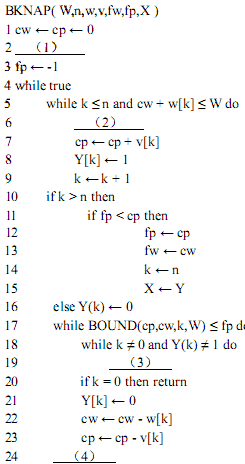 正确答案:
正确答案:
(1)k←1或其等价形式(2)cw←cw+w[k]或其等价形式(3)k←k–1或其等价形式(4)k←k+l或其等价形式 -
第17题:
阅读以下说明和C代码,填补代码中的空缺,将解答填入答题纸的对应栏内。【说明】二叉查找树又称为二叉排序树,它或者是一棵空树,或者是具有如下性质的二叉树。(1)若它的左子树非空,则左子树上所有结点的值均小于根结点的值。(2)若它的右子树非空,则右子树上所有结点的值均大于根结点的值。(3)左、右子树本身就是两棵二叉查找树。二叉查找树是通过依次输入数据元素并把它们插入到二叉树的适当位置上构造起来的,具体的过程是:每读入一个元素,建立一个新结点,若二叉查找树非空,则将新结点的值与根结点的值相比较,如果小于根结点的值,则插入到左子树中,否则插入到右子树中;若二叉查找树为空,则新结点作为二叉查找树的根结点。根据关键码序列{46,25,54,13,29,91}构造一个二叉查找树的过程如图4-1所示。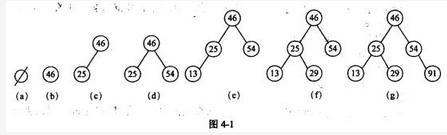
设二叉查找树采用二叉链表存储,结点类型定义如下:
typedef int KeyType;typedef struct BSTNode{KeyType key;struct BSTNode *left,*right;}BSTNode,*BSTree;
图4-1(g)所示二叉查找树的二叉链表表示如图4-2所示。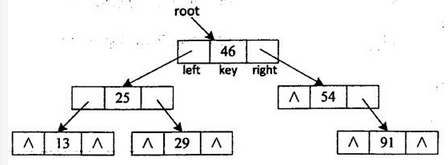
函数int InsertBST(BSTree *rootptr,KeyType kword)功能是将关键码kword插入到由rootptr指示出根结点的二叉查找树中,若插入成功,函数返回1,否则返回0。【C代码】
int lnsertBST(BSTree*rootptr,KeyType kword)/*在二叉查找树中插入一个键值为kword的结点,若插入成功返回1,否则返回0;*rootptr为二叉查找树根结点的指针*/{BSTree p,father;(1) /*将father初始化为空指针*/p=*rootptr; /*p指示二叉查找树的根节点*/while(p&&(2)){ /*在二叉查找树中查找键值kword的结点*/father=p;if(kword<p->key)p=p->left;elsep=p->right;}if((3))return 0; /*二叉查找树中已包含键值kword,插入失败*/ p=(BSTree)malloc((4)); /*创建新结点用来保存键值kword*/If(!p)return 0; /*创建新结点失败*/p->key=kword;p->left=NULL;p->right=NULL; If(!father)(5) =p; /*二叉查找树为空树时新结点作为树根插入*/elseif(kword<father->key)(6);/*作为左孩子结点插入*/else(7);/*作右孩子结点插入*/return 1;}/*InsertBST*/答案:解析:father=(void*)0keyword!=p-keypsizeof(BSTNode)*rootptrfather-left=pfather-right=p -
第18题:
对下图所示的二叉树进行顺序存储(根结点编号为1,对于编号为i的结点,其左孩子结点为2i,右孩子结点为2i+1)并用一维数组BT来表示。已知结点X、E和D在数组BT中的下标为分别为1、2、3,可推出结点G、K和H在数组BT中的下标分别为( )。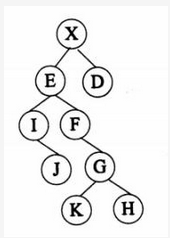 A.10、11、12
A.10、11、12
B.12、24、25
C.11、12、13
D.11、22、23答案:D解析:按照“左孩子结点为2i,右孩子结点为2i+1”,且E=2的原则带入图中元素计算。 -
第19题:
一棵二叉树顺序编号为6的结点(树中各结点的编号与等深度的完全二叉树中对应位置上结点的编号相同),若它存在右孩子,则右孩子的编号为()。
13
略 -
第20题:
下面关于哈夫曼树的说法,不正确的是()
- A、对应于一组权值构造出的哈夫曼树一般不是唯一的
- B、哈夫曼树具有最小带权路径长度
- C、哈夫曼树中没有度为1的结点
- D、哈夫曼树中除了度为1的结点外,还有度为2的结点和叶结点
正确答案:D -
第21题:
简述顺序表示的二叉树中各结点的编号规则。
正确答案:顺序表示的二叉树中各结点的编号与相同深度的完全二叉树中对应结点的编号相同。 -
第22题:
有这样一类特殊0-1背包问题:可选物品重量越轻的物品价值越高。 n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大,能获得的最大总价值多少?
正确答案: 因为该0-1背包问题比较特殊,恰好重量越轻的物品价值越高,所以优先取重量轻的物品放进背包。最终可以把重量分别为2,3,4,5的三个物品放进背包,得到的价值和为15+8+6+4=33,为最大值。 -
第23题:
问答题简述顺序表示的二叉树中各结点的编号规则。正确答案: 顺序表示的二叉树中各结点的编号与相同深度的完全二叉树中对应结点的编号相同。解析: 暂无解析

