表1-2中,第1行依次列出了0.00,0.01,0.02,0.03,…,0.99,共100个数据;对第1行的每个数据采用方法1(通常的四舍五入法)处理后形成第2行数据:对第1行的每个数据采用方法2(修改后的四舍五入法)处理后形成第3行数据。通过对表1-2三行数据分别求算术平均值,可以看出:在处理表1-2的数据时,方法1与方法2相比,(65)。A.方法1产生偏低结果,方法2不会产生统计偏差B.方法1产生偏高结果,方法2产生偏低结果C.方法1产生偏高结果,方法2不会产生统计偏差D.方法1不会产生统计偏差,方法
题目
表1-2中,第1行依次列出了0.00,0.01,0.02,0.03,…,0.99,共100个数据;对第1行的每个数据采用方法1(通常的四舍五入法)处理后形成第2行数据:对第1行的每个数据采用方法2(修改后的四舍五入法)处理后形成第3行数据。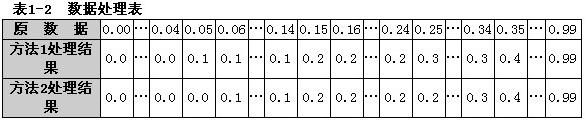
通过对表1-2三行数据分别求算术平均值,可以看出:在处理表1-2的数据时,方法1与方法2相比,(65)。
A.方法1产生偏低结果,方法2不会产生统计偏差
B.方法1产生偏高结果,方法2产生偏低结果
C.方法1产生偏高结果,方法2不会产生统计偏差
D.方法1不会产生统计偏差,方法2产生偏低结果
相似考题
更多“ 表1-2中,第1行依次列出了0.00,0.01,0.02,0.03,…,0.99,共100个数据;对第1行的每个数据采用方法1(通常的四舍五入法)处理后形成第2行数据:对第1行的每个数据采用方法2(修改后的四舍五”相关问题
-
第1题:
下表中,第一行依次列出了0.00,0.01,0.02,0.03,…,0.99,共100个数据;对第一行的每个数据采用方法1处理后形成第二行数据;对第一行的每个数据采用方法2处理后形成第三行数据。

方法1是对末位数字采用4舍5入处理,即末位数字是4或4以下时舍去,若末位数字是5或5以上,则进1。 方法2对4舍5入法做了如下修改:如果末位数字是5,则并不总是入,而需要根据前一位数字的奇偶性再决定舍入:如果前一位数字是偶数,则将5舍去;如果前一位数字是奇数,则进1。例如,0.05将舍入成0.0;0.15将舍入成0.2。 通过对这三行数据分别求算术平均值,可以看出:在处理一批正数时,方法1(通常的4舍5入法)与方法2(修改后的4舍5入法)相比,(65)。
A.方法1与方法2都不会产生统计偏差(舍与入平均相抵)
B.方法1不会产生统计偏差,方法2产生偏高结果
C.方法1产生偏低结果,方法2不会产生统计偏差
D.方法1产生偏高结果,方法2改进了方法1
正确答案:D
解析:单纯解答本题并不难。第一行100个数据都是正数,均匀地列出了2位小数的各种可能,其平均值为49.50。经方法1处理后的100个数据的平均值为50.00,可以看出,方法1产生了偏高结果;经方法2处理后的100个数据的平均值为49.50,可以看出,方法2改进了方法1。
本题的意义是:对处理大批正数而言,4舍5入方法比较简单实用,但也比较粗略,会产生略微偏高的结果。在需要更精确要求的应用领域,采用方法2更好些。
实际工作中采集的数据大多是正数,而且大多是近似值,小数点后太多的位数没有实际意义。为了使计算结果精确到小数点后某一位,原始数据就应在小数点后多取1位。计算完成后,常需要对小数点后最末一位数字进行舍入处理。
人们通常使用4舍5入法对最末位数字进行舍入处理。4以下的数字则舍去,5以上的数字则需要进1。这种做法确实简单实用,但从下表可以看出,平均而言,舍的量略低于入的量。
其中,0.4舍的量与0.6入的量可以相抵,0.3舍的量与0.7入的量可以相抵……。正数4舍5入的偏差来自尾数为5的量都要进位,从而产生偏高结果。为平衡起见,应将尾数为5的情况分裂成两种情况:有一半的可能需要舍,有一半的可能需要入。方法 2规定,经舍入后应保持新的尾数为偶数,这有—半的可能。当然,如果规定新的尾数应成为奇数,也是可以的。但在同一个问题的计算过程中,总是要有统一的规定。保持偶数比保持奇数对进一步计算(例如再分半)会更有利些,所以人们选用方法2来改进方法1。
在银行利息计算中,采用粗略的方法还是采用更精细的方法可能会有较大一笔钱的出入。
对于正负数对称分布的情况,则4舍5入法不会产生偏差。因为正数的舍(引起减少)与负数的舍(引起增加)相抵,正数的入(引起增加)与负数的入(引起减少)相抵。
从本题也可以看出,在信息处理领域人们不但要学会使用数据处理的软件,更需要研究数据处理领域本身的技术。 -
第2题:
head(data[, 1:3])显示数据库的()。
A.第1列,第3列数据
B.第1行和第3行数据
C.第1至3列数据
D.第1至3行数据
第1至3列数据 -
第3题:
1. 创建并访问DataFrame对象。 1) 创建3×3DataFrame数据对象:数据内容为1-9;行索引为字符a,b,c;列索引为字符串‘one’,‘two’,‘three’; 2) 查询列索引为‘two’和‘three’两列数据; 3) 查询第0行、第2行、第0列、第2列数据; 4) 筛选第1列中值大于2的所有行数据,另存为data1对象; 5) 为data1添加一列数据,列索引为‘four’,值都为10; 6) 将data1所有值大于9的数据修改为8; 7) 删除data1中第0行和第1行数据。
t;>>data=[[4,5,6], [4,5,6], [4,5,6]];t;>>df=pd.DataFrame(data,columns=list(‘ABC’));以将df中值为5的数据修改为10的语句是:};df[df.values==5]=10 -
第4题:
有一个3行3列的数据框xx,对xx的两列数据进行排序,xx[order(xx[ , 2], -xx[ , 3]) ,] 的结果为:
A.第2列升序,第3列降序
B.第2列升序,第3列升序
C.第2列降序,第3列升序
D.第2列降序,第3列降序
第 2 列升序,第 3 列降序 -
第5题:
下列选项中属于对线性表进行插入操作的是()
A.将第i+1到第size-1索引位置上数据元素(共size-1-i个数据元素)依次前移。#B.清除最后一个数据元素的值,使顺序表的表长度size减1。#C.将索引位置为i~size-1存储位置上的元素(共size-i个数据元素)依次后移后,将新的数据元素置于i位置上#D.以上都是将索引位置为i~size-1 存储位置上的元素(共 size-i 个数据元素)依次后移后,将新的数据元素置于 i 位置上
