阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。【说明】对于大于1的正整数n,(x+1)n可展开为下面流程图的作用是计算(x+1)n展开后的各项系数(i=0,1,....,n)并依次存放在数组A[0...n]中。方法是依次计算k=2,3,..,n时(x+1)k的展开系数并存入数组A,在此过程中,对任一确定的k,利用关系式,按照i递减的顺序逐步计算并将结果存储在数组A中。其中,和都为1,因此可直接设置A[0]、A[k]的值为1。 例如,计算(x+1)3的过程如下:先计算(x+1)2(即
题目
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。
【说明】对于大于1的正整数n,(x+1)n可展开为下面流程图的作用是计算(x+1)n展开后的各项系数(i=0,1,....,n)并依次存放在数组A[0...n]中。方法是依次计算k=2,3,..,n时(x+1)k的展开系数并存入数组A,在此过程中,对任一确定的k,利用关系式,按照i递减的顺序逐步计算并将结果存储在数组A中。其中,和都为1,因此可直接设置A[0]、A[k]的值为1。 例如,计算(x+1)3的过程如下:先计算(x+1)2(即k=2)的各项系数,然后计算(x+1)3(即k=3)的各项系数。K=2时,需要计算,和,并存入A[0],A[1]和A[2],其中A[0]和A[1]的值已有,因此将(即A[1])和即(A[0])相加得到的值并存入A[1]。k=3时,需要计算,和和,先计算出(由)得到并存入A[2],再计算(由得到)并存入A[1]。
相似考题
更多“阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。【说明】对于大于1的正整数 ”相关问题
-
第1题:
阅读以下说明和Java程序,填补代码中的空缺(1)~(6),将解答填入答题纸的
对应栏内。
【说明】
很多依托扑克牌进行的游戏都要先洗牌。下面的Java代码运行时先生成一副扑克
牌,洗牌后再按顺序打印每张牌的点数和花色。
【Java代码】

 正确答案:
正确答案:
本题考查Java语言程序设计的能力,涉及类、对象、方法的定义和相关操作。要求考生根据给出的案例和代码说明,认真阅读,理清程序思路,然后完成题目。先考查题目说明。本题目中涉及到扑克牌、牌桌、玩家等类以及洗牌和按点数排序等操作。根据说明进行设计。Card类内定义了两个static枚举类型,Face枚举扑克牌点数,Suit枚举扑克牌花色。Card类有两个枚举类型的属性,face和suit,而且值不再变化,故用final修饰。在使用构造方法publicCard(Faceface,Suitsuit)新建一个Car:d的对象时,所传入的参数指定face和suit这两个属性值。因为参数名称和属性名称相同,所以用this前缀区分出当前对象。在类Card中包含方法getFace()和getSuit(),分别返回当前对象的face和suit属性值。getCard()方法返回string来表示一张牌,包括扑克牌点数和花色。牌桌类Deckofcands包含持有Card类型元素的List类型对象的声明List,用以存储牌。List是Java中的一种集合接口,是Collection的子接口。构造方法中用Card对象填充牌桌并进行洗牌。先用Card对象填充牌桌,即创建52个Card对象加入deck数组,表示牌桌上一副牌(52张)。然后洗牌,即将数组中的Card对象根据花色和点数随机排列,使用集合工具类Collechons中的shuffle方法,对以List类型表示的deck数组进行随机排列。Collectians是Java集合框架中两个主要工具类之一,用以进行集合有关的操作。printCards()方法将所有Card对象打印出来,按4列显示52张牌。每张拍的打印用list.get(i)获得list表示的deck中的第i个Card对象,然后进一步调用此对象的getCard()方法,得到String表示的当前一张牌。玩家类中包括启动发牌洗牌等操作,主入口方法main中实现创建牌桌对象,并调用按4列显示52张牌。在main()中,先初始化Deckofcards类的对象player,即生成一个牌桌:Deckofcardsplayer=newDeckofcards()并发牌,即调用player的printCards()方法,实现按4列显示52张牌打印一副扑克牌中每张牌的点数和花色。在pnntCards()方法体内部,用list调用每个数组元素,井为每个数组元素调用getCard()返回当前对象所表示一张牌的花色和点数。用格式化方法进行打印,即:因此,主(1)和(2)需要表示当前对象的this.;空(3)需要牌桌上纸牌对象,并将数组元素下标加1,即数组元素deck[count++];空(4)也需要用list对象获得纸牌对象的字符串表示,即list后的get(1)getCard();空(5)处为创建DeckOf℃ards类的对象指针player的newDeckOfCards();空(6)需要用对象player调用打印所有纸牌的printCards()函数,即player.。试题六参考答案(l)this(2)this.(3)deck[count++]或等价表示(4)get(i)getCard()(5)newDeckOfCards()(6)player. -
第2题:
阅读说明和流程图,填补流程图中的空缺(1)?(5),将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1,a2=1,…,an=an-1+an-2!n=3,4,…}的前n项(n>=2) 之和S。例如,菲波那契数列前6项之和为20。计算过程中,当前项之前的两项分别动态地保存在变量A和B中。【流程图】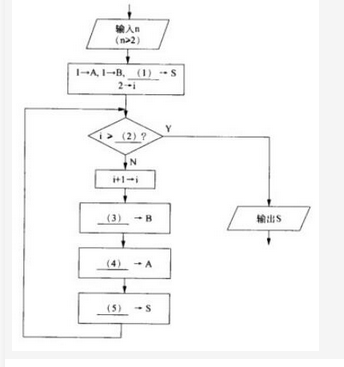 答案:解析:(1)2或A+B(2)n(3)A+B(4)B-A(5)S+B
答案:解析:(1)2或A+B(2)n(3)A+B(4)B-A(5)S+B
【解析】
菲波那契数列的特点是首2项都是1,从第3项开始,每一项都是前两项之和。该数列的前几项为1,1,2, 3,5,8,…。在流程图中,送初始值1—A,2—B后,显然前2项的和S应等于2,所以(1)处应填2 (或A+B)。此时2→i (i表示动态的项编号),说明已经计算出前2项之和。接着判断循环的结束条件。显然当i=n时表示已经计算出前n项之和,循环可以结束了。因此(2)处填n。判断框中用“>”或“≥”的效果是一样的,因为随着i的逐步增1,只要有i=n结束条件就不会遇到i>n的情况。不过编程的习惯使循环结束条件扩大些,以防止逻辑出错时继续循环。接下来i+1→i表示数列当前项的编号增1,继续往下计算。原来的前两项值(分别在变量A和B中)将变更成新的前两项再放到变量A和B中。
首先可以用A+B—B实现(原A) + (原B)—(新B),因此(3)处填A+B。为了填新A值(原来的B值),不能用B—A,因为变量B的内容已经改变为(原A) + (原B),而B-A正是((原A) + (原B))-(原A)=(原B),因此可以用B-A—A来实现新A的赋值。这样,(4)处填B-A。最后应是前n项和值的累加(比原来的S值增加了新B值),所以(5)处应填S+B。填完各个空后,最好再用具体的数值来模拟流程图走几个循环检查所填的结果(这是防止逻辑上出错的好办法)。 -
第3题:
阅读下列说明,补充(1)-(9),将解答填入答题纸的对应栏内。 答案:解析:
答案:解析:
-
第4题:
阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。
[说明]
本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾依次分离出各个关键词{A(i)|i=1,…,n}(n>1)},其中包含了很多重复项,经下面的流程处理后,从中挑选出所有不同的关键词共m个{K(j)|j=1,…,m},而每个关键词K(j)出现的次数为NK(j),j=1,…,m。
[流程图]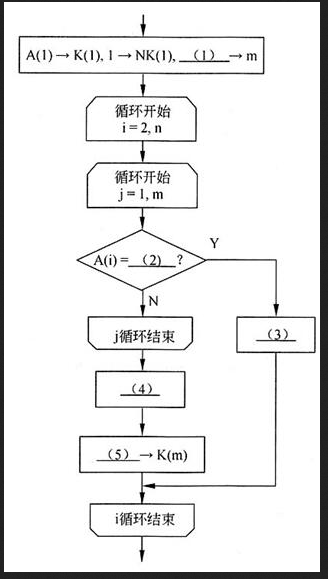 答案:解析:1
答案:解析:1
K(j)
NK(j)+1→NK(i) 或NK(j)++ 或等价表示
m+1→m或m++ 或等价表示
A(i)
【解析】
流程图中的第1框显然是初始化。A(1)→K(1)意味着将本书的第1个关键词作为选出的第1个关键词。1→NK(1)意味着此时该关键词的个数置为1。m是动态选出的关键词数目,此时应该为1,因此(1)处应填1。
本题的算法是对每个关键词与已选出的关键词进行逐个比较。凡是遇到相同的,相应的计数就增加1;如果始终没有遇到相同关键词的,则作为新选出的关键词。
流程图第2框开始对i=2,n循环,就是对书中其他关键词逐个进行处理。流程图第3框开始j=1,m循环,就是按己选出的关键词依次进行处理。
接着就是将关键词A(i)与选出的关键词K(j)进行比较。因此(2)处应填K(j)。
如果A(i)=K(i),则需要对计数器NK(j)增1,即执行NK(j)+1→NK(j)。因此(3)处应填NK(j)+1→NK(j)。执行后,需要跳出j循环,继续进行i循环,即根据书中的下一个关键词进行处理。
如果A(i)不等于NK(j),则需要继续与下个NK(j)进行比较,即继续执行j循环。如果直到j循环结束仍没有找到匹配的关键词,则要将该A(i)作为新的已选出的关键词。因此,应执行A(i)→K(m+1)以及m+1→m。更优的做法是先将计数器m增1,再执行A(i)→K(m)。因此(4)处应填m+1→m,(5)处应填A(i)。 -
第5题:
第一题 阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。
【说明】
对于大于1的正整数n,(x+1)n可展开为
问题:1.1 【流程图】
注:循环开始框内应给出循环控制变量的初值和终值,默认递增值为1。
格式为:循环控制变量=初值,终值,递增值。答案:解析:(1)2,n,1
(2)A[k]
(3)k-1,1,-1
(4)A[i]+A[i-1]
(5)A[i]
【解析】
(1)(3)空为填写循环初值终值和递增值,题目中给出的格式为循环控制变量=初值,终值,递增值。按照题意,实质为求杨辉三角。如下图: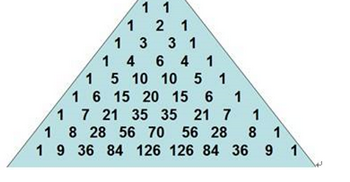

-
第6题:
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。【说明】设[a1b1],[a2b2],...[anbn]是数轴上从左到右排列的n个互不重叠的区间(a1 答案:解析:1.A2.ai3.bi4.A 、B5.B
答案:解析:1.A2.ai3.bi4.A 、B5.B
【解析】
若A≤ai则输出A,反之输出ai。若A≤bi不满足则输出bi,依次类推。
