某二叉树如图所示，若进行顺序存储（即用一维数组元素存储该二叉树中的结点且通过下标反映结点间的关系，例如，对于下标为i的结点，其左孩子的下标为2i、右孩子的下标为2i+1），则该数组的大小至少为（请作答此空）；若采用三叉链表存储该二叉树（各个结点包括结点的数据、父结点指针、左孩子指针、右孩子指针），则该链表的所有结点中空指针的数目为（ ）。 A.6 B.10 C.12 D.15
题目
B.10
C.12
D.15
相似考题
参考答案和解析
可见，空指针的数目为8。
更多“某二叉树如图所示，若进行顺序存储（即用一维数组元素存储该二叉树中的结点且通过下标反映结点间的关系，例如，对于下标为i的结点，其左孩子的下标为2i、右孩子的下标为2i+1），则该数组的大小至少为（请作答此空）；若采用三叉链表存储该二叉树（各个结点包括结点的数据、父结点指针、左孩子指针、右孩子指针），则该链表的所有结点中空指针的数目为（ ）。 A.6 B.10 C.12 D.15”相关问题
-
第1题：
二叉树如右图所示,若进行顺序存储（即用一维数组元素存储该二叉树中的结点且通过下标反映结点间的关系，例如，对于下标为i的结点，其左孩子的下标为2i、右孩子的下标为2i+1），则该数组的大小至少为（ ）；若釆用三叉链表存储该二叉树（各个结 点包括结点的数据、父结点指针、左孩子指针、右孩子指针），则该链表的所有结点中空指针的数目为（ ）。
A.6 B.10 C.12 D.15 A.6 B.8 C.12 D.14
正确答案：D,B
-
第2题：
某二叉树如图所示，若进行顺序存储（即用一维数组元素存储该二叉树中的节点且通过下标反映节点间的关系，例如，对于下标为i的节点，其左孩子的下标为2i、右孩子的下标为2i+1），则该数组的大小至少为 （请作答此空） ；若采用三叉链表存储该二叉树（各个节点包括节点的数据、父节点指针、左孩子指针、右孩子指针），则该链表的所有节点中空指针的数目为 （ ） 。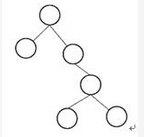
A.6
B.10
C.12
D.15答案：D解析：采用顺序存储结构存储二叉树时，一般的二叉树也必须按照完全二叉树的形式存储，需要填上一些不存在的"虚节点"。题中二叉树的高度为4，需要的存储空间为24-1=15，如下：
可见，空指针的数目为8。 -
第3题：
在二叉树的顺序存储中，每个结点的存储位置与其父结点、左右子树结点的位置都存在一个简单的映射关系，因此可与三叉链表对应。若某二叉树共有n个结点，采用三叉链表存储时，每个结点的数据域需要d个字节，每个指针域占用4个字节，若采用顺序存储，则最后一个结点下标为k(起始下标为1)，采用顺序存储更节省空间的情况是()。A.d＜12n/(k-n)
B.d＞12n/(k-n)
C.d＜12n/(k+n)
D.d＞12n/(k+n)答案：A解析：
-
第4题：
对下图所示的二叉树进行顺序存储（根结点编号为1,对于编号为i的结点,其左孩子结点为2i,右孩子结点为2i+1）并用一维数组BT来表示,已知结点X、E和D在数组BT中的下标分别为1、2、3,可推出结点G、K和H在数组BT中的下分别为（ ）。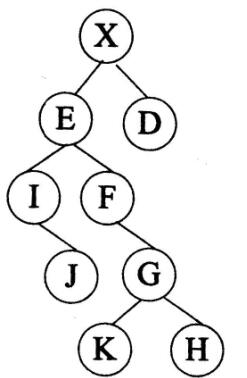
A.10、11、12
B.12、24、25
C.11、12、13
D.11、22、23答案：D解析：元素G为F的右子树,其下标为2F+1 ; F为元素E的右子树,其下标为2E+1, E的下标为2，因此G=2* (2*2+1) +1=11 ; K=2G=22 ; H=2G+1=23 ; -
第5题：
若用链表存储一棵二叉树时，每个结点除数据域外，还有指向左孩子和右孩子的两个指针。在这种存储结构中有（）个指针是空指针。
正确答案:n+1 -
第6题：
若对一棵二叉树从0开始进行结点编号，并按此编号把它顺序存储到一维数组a中，即编号为0的结点存储到a[0]中，其余类推，则a[i]元素的左孩子元素为（），右孩子元素为（），双亲元素（i>0）为（）。
正确答案:A[2*i+1]；a[2*i+2]；a[i/2] -
第7题：
在对二叉树进行顺序存储时，若下标为6的结点P既有双亲结点，又有左孩子结点和右孩子结点，则P的双亲结点的下标为（），左孩子结点的下标为（），右孩子结点的下标为（）
正确答案:3；12；13 -
第8题：
在完全二叉树中，若一个结点是叶结点，则它没有（）。
- A、左孩子结点
- B、右孩子结点
- C、左孩子和右孩子结点
- D、左孩子结点，右孩子结点和兄弟结点
正确答案:C -
第9题：
填空题假定一棵二叉树顺序存储在一维数组a中，但让编号为1的结点存入a[0]元素中，让编号为2的结点存入a[1]元素中，其余类推，则编号为i结点的左孩子结点对应的存储位置为（），若编号为i结点的存储位置用j表示，则其左孩子结点对应的存储位置为（）正确答案： 2i-1,2j+1解析： 暂无解析 -
第10题：
填空题若用链表存储一棵二叉树时，每个结点除数据域外，还有指向左孩子和右孩子的两个指针。在这种存储结构中有（）个指针是空指针。正确答案： n+1解析： 暂无解析 -
第11题：
填空题若用链表存储一棵二叉树时，每个结点除数据域外，还有指向左孩子和右孩子的两个指针。在这种存储结构中，n个结点的二叉树共有（）个指针域。正确答案： 2n解析： 暂无解析 -
第12题：
填空题若对一棵二叉树从0开始进行结点编号，并按此编号把它顺序存储到一维数组a中，即编号为0的结点存储到a[0]中，其余类推，则a[i]元素的左孩子元素为（），右孩子元素为（），双亲元素（i>0）为（）。正确答案： A[2*i+1],a[2*i+2],a[i/2]解析： 暂无解析 -
第13题：
当有7个结点的二叉树采用二叉链表链存储时，空指针的个数为（请作答此空），采用三叉链表存储空指针的个数为（ ）。A.6
B7
C8
D9答案：C解析：结果如图所示，空指针个数分别为结点数加1，与结点数加2。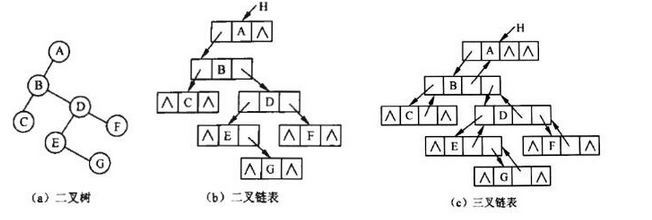
-
第14题：
对下图所示的二叉树进行顺序存储(根结点编号为1,对于编号为i的结点，其左孩子结点为2i,右孩子结点为2i+1)并用一维数组BT来表示。已知结点X、E和D在数组BT中的下标为分别为1、2、3,可推出结点G、K和H在数组BT中的下标分别为（ ）。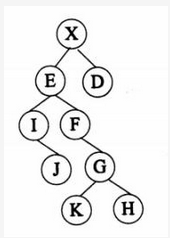
A.10、11、12
B.12、24、25
C.11、12、13
D.11、22、23答案：D解析：按照“左孩子结点为2i,右孩子结点为2i+1”，且E=2的原则带入图中元素计算。 -
第15题：
某二叉树如图所示，若进行顺序存储(即用一维数组元素存储该二叉树中的结点且通过下标反映结点间的关系，例如，对于下标为i的结点，其左孩子的下标为2i、右孩子的下标为2i+1)，则该数组的大小至少为（58）；若采用三叉链表存储该二叉树(各个结点包括结点的数据、父结点指针、左孩子指针、右孩子指针)，则该链表的所有结点中空指针的数目为（59）。A.6
B.8
C.12
D.14答案：B解析：采用顺序存储结构存储二叉树时，一般的二叉树也必须按照完全二叉树的形式存储，需要填上一些不存在的“虚结点”。题中二叉树的高度为4，需要的存储空间为24-1=15，如下：可见，空指针的数目为8。 -
第16题：
若用链表存储一棵二叉树时，每个结点除数据域外，还有指向左孩子和右孩子的两个指针。在这种存储结构中，n个结点的二叉树共有（）个指针域。
正确答案:2n -
第17题：
若用链表存储一棵二叉树时，每个结点除数据域外，还有指向左孩子和右孩子的两个指针。在这种存储结构中，有（）个指针域是存放了地址。
正确答案:n-1 -
第18题：
假定一棵二叉树顺序存储在一维数组a中，但让编号为1的结点存入a[0]元素中，让编号为2的结点存入a[1]元素中，其余类推，则编号为i结点的左孩子结点对应的存储位置为（），若编号为i结点的存储位置用j表示，则其左孩子结点对应的存储位置为（）。
正确答案:2i-1；2j+1 -
第19题：
线索链表中的rtag域值为（）时，表示该结点无右孩子，此时（）域为指向该结点后继线索的指针。
正确答案:1；RChild -
第20题：
对于一棵具有n个结点的二叉树，采用二叉链表存储时，链表中指针域的总数为（）个，其中（）个用于链接孩子结点，（）个空闲着。
正确答案:2n；n-1；n+1 -
第21题：
填空题在对二叉树进行顺序存储时，若下标为6的结点P既有双亲结点，又有左孩子结点和右孩子结点，则P的双亲结点的下标为（），左孩子结点的下标为（），右孩子结点的下标为（）正确答案： 3,12,13解析： 由二叉树的性质⑤可知，若对任一完全二叉树上的所有结点按层从左向右编号，则结点编号之间的数值关系可以准确地反映结点之间的逻辑关系。因此，对于完全二叉树的顺序存储来说，采用的是“以编号为地址”的策略将结点存入作为顺序存储结构的一维数组，即将编号为i的结点存入一维数组的第i个单元。利用二叉树的性质⑤可求出结果 -
第22题：
单选题将森林F转换为对应的二叉树T，F中叶结点的个数等于（）AT中叶结点的个数
BT中度为1的结点个数
CT中左孩子指针为空的结点个数
DT中右孩子指针为空的结点个数
正确答案： B解析： -
第23题：
填空题对于一棵具有n个结点的二叉树，采用二叉链表存储时，链表中指针域的总数为（）个，其中（）个用于链接孩子结点，（）个空闲着。正确答案： 2n,n-1,n+1解析： 暂无解析