阅读以下说明和C函数,将应填入(n)处的字句写在对应栏内。【说明】已知某二叉树的非叶子结点都有两个孩子结点,现将该二叉树存储在结构数组Ht中。结点结构及数组Ht的定义如下:define MAXLEAFNUM 30struct node{char ch; /*当前结点表示的字符,对于非叶子结点,此域不用*/char *pstr; /*当前结点的编码指针,非叶子结点不用*/int parent; /*当前结点的父结点,为0时表示无父结点*/int lchild,rchild;/*当前结点的左、右孩子结点,为0
题目
阅读以下说明和C函数,将应填入(n)处的字句写在对应栏内。
【说明】
已知某二叉树的非叶子结点都有两个孩子结点,现将该二叉树存储在结构数组Ht中。结点结构及数组Ht的定义如下:
define MAXLEAFNUM 30
struct node{
char ch; /*当前结点表示的字符,对于非叶子结点,此域不用*/
char *pstr; /*当前结点的编码指针,非叶子结点不用*/
int parent; /*当前结点的父结点,为0时表示无父结点*/
int lchild,rchild;
/*当前结点的左、右孩子结点,为0时表示无对应的孩子结点*/
};
struct node Ht[2*MAXLEAFNUM]; /*数组元素Ht[0]不用*/
该二叉树的n个叶子结点存储在下标为1~n的Ht数组元素中。例如,某二叉树如果其存储结构如下图所示,其中,与叶子结点a对应的数组元素下标为1,a的父结点存储在Ht[5],表示为Ht[1].parent=5。Ht[7].parent=0表示7号结点是树根,Ht[7].child=3、Ht[7].rchild=6分别表示7号结点的左孩子是3号结点、右孩子是6号结点。
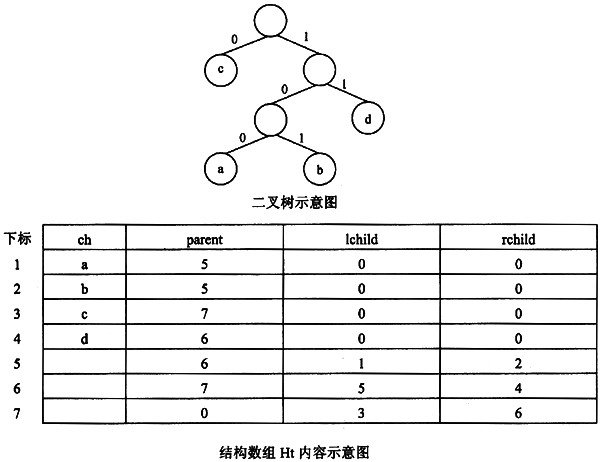
如果用0或1分别标识二叉树的左分支和右分支(如上图所示),从根结点开始到叶子结点为止,按所经过分支的次序将相应标识依次排列,可得到一个0、1序列,称之为对应叶子结点的编码。例如,上图中a,b,c,d的编码分别是100,101,0,11。
函数LeafCode(Ht[],n)的功能是:求解存储在Ht中的二叉树中所有叶子结点(n个)的编码,叶子结点存储在Ht[1]~Ht[n]中,求出的编码存储区由对应的数组元素pstr域指示。
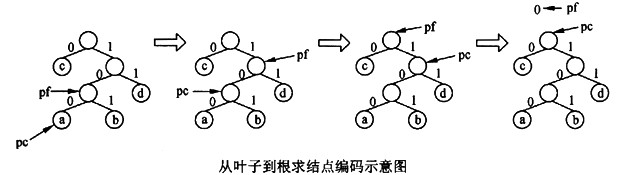
函数LeafCode从叶子到根逆向求叶子结点的编码。例如,对上图中叶子结点a求编码的过程如下图所示。
typedef enum Status {ERROR,OK} Status;
【C函数】
Status LeafCode(struct node Ht[], int n)
{
int pc, pf; /*pc用于指出树中的结点,pf则指出pc所对应结点的父结点*/
int i,start;
char tstr[31] = {'\0'}; /*临时存储给定叶子结点的编码,从高下标开始存入*/
for(i = 1;(1); i++){ /*对所有叶子结点求编码,i表示叶结点在HT数组中的下标*/
start = 29;
pc = i; pf = Ht[i].parent;
while (pf !=(2)) { /*没有到达树根时,继续求编码*/
if ((3).lchild == pc ) /*pc所表示的结点是其父结点的左孩子*/
tstr[--start] = '0';
else
tstr[--start] = '1';
pc =(4); pf = Ht[pf].parent; /*pc和pf分别向根方向回退一层*/
}/* end of while */
Ht[i].pstr = (char *) malloc(31-start);
if (!Ht[i].pstr) return ERROR;
strcpy(Ht[i].pstr,(5));
}/* end of for */
return OK;
}/* and of LeafCode */
相似考题
更多“ 阅读以下说明和C函数,将应填入(n)处的字句写在对应栏内。【说明】已知某二叉树的非叶子结点都有两个孩子结点,现将该二叉树存储在结构数组Ht中。结点结构及数组Ht的定义如下:define MAXLEAFNUM 30”相关问题
-
第1题:
阅读以下预备知识、函数说明和C代码,将应填入(n)处的字句写在对应栏内。
[预备知识]
①对给定的字符集合及相应的权值,采用哈夫曼算法构造最优二叉树,并用结构数组存储最优二叉树。例如,给定字符集合{a,b,c,d}及其权值2、7、4、5,可构造如图3所示的最优二叉树和相应的结构数组Ht(数组元素Ht[0]不用)(见表5)。

结构数组HT的类型定义如下:
define MAXLEAFNUM 20
struct node {
char ch; / * 当前结点表示的字符,对于非叶子结点,此域不用*/
int weight; / * 当前结点的权值*/
int parent; / * 当前结点的父结点的下标,为0时表示无父结点*/
int Ichild, rchild
/ *当前结点的左、右孩子结点的下标,为0时表示无对应的孩子结点* /
} Ht[2 * MAXLEAFNUM];
②用'0'或'1'标识最优二叉树中分支的规则是:从一个结点进入其左(右)孩子结点,就用'0'('1')标识该分支(示例如图3所示)。
③若用上述规则标识最优二叉树的每条分支后,从根结点开始到叶子结点为止,按经过分支的次序,将相应标识依次排列,可得到由'0'、'1'组成的一个序列,称此序列为该叶子结点的前缀编码。如图3所示的叶子结点a、b、c、d的前缀编码分别是110、0、111、10。
【函数5.1说明】
函数void LeafCode (int root, int n)的功能是:采用非递归方法,遍历最优二叉树的全部叶子结点,为所有的叶子结点构造前缀编码。其中形参root为最优二叉树的根结点下标;形参 n为叶子结点个数。
在构造过程中,将Ht[p]. weight域用作被遍历结点的遍历状态标志。
【函数5.1】
char * * Hc;
void LeafCode (int root, int n)
{/*为最优二叉树中的n个叶子结点构造前缀编码,root是树的根结点下标* /
int i,p = root,cdlen =0;char code[20];
Hc=(char* * )malloc(.(n +]) *sizeof(char* )); /* 申请字符指针数组* /
for(i=1;i< =p;++i)
Ht[ i]. weight =0;/* 遍历最优二叉树时用作被遍历结点的状态标志*/
while(p) {/*以非递归方法遍历最优二叉树,求树中每个叶子结点的编码*/
if(Ht[p], weight ==0) { /*向左*/
Ht[ p]. weight =1
if (Ht[p],lchild !=0) { p=Ht[P].lchild; code[cdlen++] ='0';]
else if (Ht[p]. rchild ==0) {/* 若是叶子结点,则保存其前缀编码*/
Hc[p] = ( char * ) malloc( (cdlen + 1 ) * sizeof (char) );
(1); strcpy(He[ p] ,code);
}
}
else if (Ht[ pi, weight == 1) { /*向右*/
Ht[p]. weight =2;
if(Ht[p].rchild !=0) {p=Ht[p].rchild; code[cdlen++] ='1';}
}
else{/* Ht[p]. weight ==2,回退*/
Ht[p]. weight =0;
p=(2);(3); /*退回父结点*/
}
}/* while结束* /
}
【函数5.2说明】
函数void Decode(char*buff, int root)的功能是:将前缀编码序列翻译成叶子结点的字符序列并输出。其中形参root为最优二叉树的根结点下标;形参buff指向前缀编码序列。
【函数5.2】
void Decode( char * buff, int root)
Iint pre =root,p;
while ( * buff! = '\0') {
p = root;
while (p!=0){/*存在下标为p的结点*/
pre=p;
if((4))p=Ht[p].lchild; /*进入左子树*/
else p = Ht[p]. rchild; / *进入右子树*./
buff ++; / * 指向前缀编码序列的下一个字符* /
}
(5);
printf("%c", Ht [ pre]. ch);
}
}
正确答案:(1)code[cdlen]='\0'或code[cdlen]=0(2)Ht[p].par- ent (3)--cdlen或等价形式(4)*buff=='0'或等价形式 (5)buff--或等价形式
(1)code[cdlen]='\0'或code[cdlen]=0(2)Ht[p].par- ent (3)--cdlen或等价形式(4)*buff=='0'或等价形式 (5)buff--或等价形式 解析:(1)根据注释的提示,可知此小段代码的作用是把code字符串保存起来,结合下一句,可知应给code字符串添加一个结束符'0'。(2)将指针指向当前结点的父结点。(3)将code指针前移一位。(4)如果前缀编码为,'0'进入左子树。(5)注意下一个语句,Prinf(“%c”,Ht[pre].ch);其参数是pre,内层循环中有pre=p,这样做的目的是当Ht[p].lchild或 Ht[p]. rchild等于0时,不把这—层链人结果。 -
第2题:
阅读以下说明和C语言函数,将应填入(n)处的字句写在对应栏内。
【说明】
下面的程序构造一棵以二叉链表为存储结构的二叉树算法。
【函数】
BTCHINALR *createbt ( BTCHINALR *bt )
{
BTCHINALR *q;
struct node1 *s [30];
int j,i;
char x;
printf ( "i,x =" ); scanf ( "%d,%c",&i,&x );
while (i!=0 && x!='$')
{ q = ( BTCHINALR* malloc ( sizeof ( BTCHINALR )); //生成一个结点
(1);
q->1child = NULL;
q->rchild = NULL;
(2);
if((3);)
{j=i/2 //j为i的双亲结点
if(i%2==0
(4) //i为j的左孩子
else
(5) //i为j的右孩子
}
printf ( "i,x =" ); scanf ( "%d,%c",&i,&x ); }
return s[1]
}
正确答案:(1)q->data=x (2) s[i]=q (3) i!=1 (4) s[j]->1child=q (5) s[j]->rchild=q
(1)q->data=x (2) s[i]=q (3) i!=1 (4) s[j]->1child=q (5) s[j]->rchild=q -
第3题:
试题三(共 15 分)
阅读以下说明和 C 程序,将应填入 (n) 处的字句写在答题纸的对应栏内。
 正确答案:
正确答案:
-
第4题:
阅读以下说明、C函数和问题,将解答填入答题纸的对应栏内。
【说明】
二叉查找树又称为二叉排序树,它或者是一棵空树,或者是具有如下性质的二叉树:
●若它的左子树非空,则其左子树上所有结点的键值均小于根结点的键值;
●若它的右子树非空,则其右子树上所有结点的键值均大于根结点的键值;
●左、右子树本身就是二叉查找树。
设二叉查找树采用二叉链表存储结构,链表结点类型定义如下:
typedefstructBiTnode{
intkey_value;/*结点的键值,为非负整数*/
structBiTnode*left,*right;/*结点的左、右子树指针*/
}*BSTree;
函数find_key(root,key)的功能是用递归方式在给定的二叉查找树(root指向根结点)中查找键值为key的结点并返回结点的指针;若找不到,则返回空指针。
【函数】
BSTreefind_key(BSTreeroot,intkey)
{
if((1))
returnNULL;
else
if(key==root->key_value)
return(2);
elseif(keykey_value)
return(3);
else
return(4);
}
【问题1】
请将函数find_key中应填入(1)~(4)处的字句写在答题纸的对应栏内。
【问题2】
若某二叉查找树中有n个结点,则查找一个给定关键字时,需要比较的结点个数取决于(5).
答案:
(1)!root,或root=0,或root==NULL
(2)root
(3)find_key(root→left,key)
(4)find_key(root→right,key)
(5)该关键字对应结点在该二叉查找树所在层次(数)或位置,或者该二叉树中从根结点到该关键字对应结点的路径长度
解析:
本题考查数据结构的应用、指针和递归程序设计。
根据二叉查找树的定义,在一棵二叉查找树上进行查找时,首先用给定的关键字与树根结点的关键字比较,若相等,则查找成功;若给定的关键字小于树根结点的关键字,则接下来到左子树上进行查找,否则接下来到右子树上进行查找。如果在给定的二叉查找树上不存在与给定关键字相同的结点,则必然进入某结点的空的子树时结束查找。因此,空(1)处填入"!root"表明进入了空树;空(2)处填入"root"表明返回结点的指针;空(3)处填入"find_key(root→left,key)"表明下一步到左子树上继续查找;空(4)处填入"find_key(root→right,key)"表明下一步到右子树上继续查找。
显然,在二叉排序树上进行查找时,若成功,则查找过程是走了一条从根结点到达所找结点的路径。例如,在下图所示的二叉排序树中查找62,则依次与46、54、101和62作了比较。因此,在树中查找一个关键字时,需要比较的结点个数取决于该关键字对应结点在该二叉查找树所在层次(数)或位置。
-
第5题:
●试题五
阅读以下预备知识、函数说明和C代码,将应填入(n)处的字句写在答题纸的对应栏内。
【预备知识】
①对给定的字符集合及相应的权值,采用哈夫曼算法构造最优二叉树,并用结构数组存储最优二叉树。例如,给定字符集合{a,b,c,d}及其权值2、7、4、5,可构造如图3所示的最优二叉树和相应的结构数组Ht(数组元素Ht[0]不用)(见表5)。

图3最优二叉树
表5 结构数组Ht

结构数组Ht的类型定义如下:
define MAXLEAFNUM 20
struct node{
char ch;/*当前结点表示的字符,对于非叶子结点,此域不用*/
int weight;/*当前结点的权值*/
int parent;/*当前结点的父结点的下标,为0时表示无父结点*/
int lchild,rchild;
/*当前结点的左、右孩子结点的下标,为0时表示无对应的孩子结点*/
}Ht[2*MAXLEAFNUM];
②用′0′或′1′标识最优二叉树中分支的规则是:从一个结点进入其左(右)孩子结点,就用′0′(′1′)标识该分支(示例如图3所示)。
③若用上述规则标识最优二叉树的每条分支后,从根结点开始到叶子结点为止,按经过分支的次序,将相应标识依次排列,可得到由′0′、′1′组成的一个序列,称此序列为该叶子结点的前缀编码。例如图3所示的叶子结点a、b、c、d的前缀编码分别是110、0、111、10。
【函数5.1说明】
函数void LeafCode(int root,int n)的功能是:采用非递归方法,遍历最优二叉树的全部叶子结点,为所有的叶子结点构造前缀编码。其中形参root为最优二叉树的根结点下标;形参n为叶子结点个数。
在构造过程中 ,将Ht[p].weight域用作被遍历结点的遍历状态标志。
【函数5.1】
char**Hc;
void LeafCode(int root,int n)
{/*为最优二叉树中的n个叶子结点构造前缀编码,root是树的根结点下标*/
int i,p=root,cdlen=0;char code[20];
Hc=(char**)malloc((n+1)*sizeof(char*));/*申请字符指针数组*/
for(i=1;i<=p;++i)
Ht[i].weight=0;/*遍历最优二叉树时用作被遍历结点的状态标志*/
while(p){/*以非递归方法遍历最优二叉树,求树中每个叶子结点的编码*/
if(Ht[p].weight==0){/*向左*/
Ht[p].weight=1;
if (Ht[p].lchild !=0) { p=Ht[p].lchild; code[cdlen++]=′0′;}
else if (Ht[p].rchild==0) {/*若是叶子结 点,则保存其前缀编码*/
Hc[p]=(char*)malloc((cdlen+1)*sizeof(char));
(1) ;strcpy(He[p],code);
}
}
else if (Ht[p].weight==1){/*向右*/
Ht[p].weight=2;
if(Ht[p].rchild !=0){p=Ht[p].rchild;code[cdlen++]=′1′;}
}
else{/*Ht[p].weight==2,回退*/
Ht[p].weight=0;
p= (2) ; (3) ;/*退回父结点*/
}
}/*while结束*/
}
【函数5.2说明】
函数void Decode(char*buff,int root)的功能是:将前缀编码序列翻译成叶子结点的字符序列并输出。其中形参root为最优二叉树的根结点下标;形参buff指向前缀编码序列。
【函数5.2】
void Decode(char*buff,int root)
{ int pre=root,p;
while(*buff!=′\0′){
p=root;
while(p!=0){/*存在下标为p的结点*/
pre=p;
if( (4) )p=Ht[p].lchild;/*进入左子树*/
else p=Ht[p].rchild;/*进入右子树*/
buff++;/*指向前缀编码序列的下一个字符*/
}
(5) ;
printf(″%c″,Ht[pre].ch);
}
}
正确答案:
●试题五【答案】(1)code[cdlen]=\0或code[cdlen]=0(2)Ht[p].parent(3)--cdlen或等价形式(4)*buff==0或等价形式(5)buff--或等价形式【解析】(1)根据注释的提示,可知此小段代码的作用是把code字符串保存起来,结合下一句,可知应给code字符串添加一个结束符/0。(2)将指针指向当前结点的父结点。(3)将code指针前移一位。(4)如果前缀编码为0进入左子树。(5)注意下一个语句,Prinf("%c",Ht[pre].ch);其参数是pre,内层循环中有pre=p,这样做的目的是当Ht[p].lchild或Ht[p].rchild等于0时,不把这一层链入结果。
