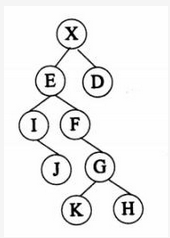
对下图所示的二叉树进行顺序存储(根结点编号为1,对于编号为i的结点，其左孩子结点为2i,右孩子结点为2i+1)并用一维数组BT来表示。已知结点X、E和D在数组BT中的下标为分别为1、2、3,可推出结点G、K和H在数组BT中的下标分别为（　）。 A.10、11、12 B.12、24、25 C.11、12、13 D.11、22、23

题目
对下图所示的二叉树进行顺序存储(根结点编号为1,对于编号为i的结点，其左孩子结点为2i,右孩子结点为2i+1)并用一维数组BT来表示。已知结点X、E和D在数组BT中的下标为分别为1、2、3,可推出结点G、K和H在数组BT中的下标分别为（　）。

A.10、11、12
B.12、24、25
C.11、12、13
D.11、22、23
相似考题

1.用数组A[1···n]顺序存储完全二叉树的各结点，则当i>0，且i<=___________时，结点A[i]的右子女是结点A[ 2i+1]，否则结点A[i]没有右子女。

2.假设一棵完全二叉树按层次遍历的顺序依次存放在数组BT[m]中,其中根结点存放在BT[0],若BT[i]中的结点有左孩子,则左孩子存放在()A.BT[i/2]B.BT[2*i-1]C.BT[2*i]D.BT[2*i+1]

3.阅读以下说明和C函数，将应填入(n)处的字句写在对应栏内。【说明】已知某二叉树的非叶子结点都有两个孩子结点，现将该二叉树存储在结构数组Ht中。结点结构及数组Ht的定义如下：define MAXLEAFNUM 30struct node{char ch; /*当前结点表示的字符，对于非叶子结点，此域不用*/char *pstr; /*当前结点的编码指针，非叶子结点不用*/int parent; /*当前结点的父结点，为0时表示无父结点*/int lchild,rchild;/*当前结点的左、右孩子结点，为0时表示无对应的孩子结点*/};struct node Ht[2*MAXLEAFNUM]; /*数组元素Ht[0]不用*/该二叉树的n个叶子结点存储在下标为1～n的Ht数组元素中。例如，某二叉树如果其存储结构如下图所示，其中，与叶子结点a对应的数组元素下标为1，a的父结点存储在Ht[5]，表示为Ht[1].parent=5。Ht[7].parent=0表示7号结点是树根，Ht[7].child=3、Ht[7].rchild=6分别表示7号结点的左孩子是3号结点、右孩子是6号结点。如果用0或1分别标识二叉树的左分支和右分支(如上图所示)，从根结点开始到叶子结点为止，按所经过分支的次序将相应标识依次排列，可得到一个0、1序列，称之为对应叶子结点的编码。例如，上图中a，b，c，d的编码分别是100，101，0，11。函数LeafCode(Ht[],n)的功能是：求解存储在Ht中的二叉树中所有叶子结点(n个)的编码，叶子结点存储在Ht[1]～Ht[n]中，求出的编码存储区由对应的数组元素pstr域指示。函数LeafCode从叶子到根逆向求叶子结点的编码。例如，对上图中叶子结点a求编码的过程如下图所示。typedef enum Status {ERROR,OK} Status;【C函数】Status LeafCode(struct node Ht[], int n){int pc, pf; /*pc用于指出树中的结点，pf则指出pc所对应结点的父结点*/int i,start;char tstr[31] = {'\0'}; /*临时存储给定叶子结点的编码，从高下标开始存入*/for(i = 1;(1); i++){ /*对所有叶子结点求编码，i表示叶结点在HT数组中的下标*/start = 29;pc = i; pf = Ht[i].parent;while (pf !=(2)) { /*没有到达树根时，继续求编码*/if ((3).lchild == pc ) /*pc所表示的结点是其父结点的左孩子*/tstr[--start] = '0';elsetstr[--start] = '1';pc =(4); pf = Ht[pf].parent; /*pc和pf分别向根方向回退一层*/}/* end of while */Ht[i].pstr = (char *) malloc(31-start);if (!Ht[i].pstr) return ERROR;strcpy(Ht[i].pstr,(5));}/* end of for */return OK;}/* and of LeafCode */

4.用顺序存储方法将完全二叉树中所有结点存放在数组R[N]中,如果结点R[i]有右子树,则该右子树的根结点为()A、R[2i+1]B、R[2i]C、R[i/2]D、R[2i+2]

参考答案和解析
答案：D
解析：
按照“左孩子结点为2i,右孩子结点为2i+1”，且E=2的原则带入图中元素计算。
更多“ 对下图所示的二叉树进行顺序存储(根结点编号为1,对于编号为i的结点，其左孩子结点为2i,右孩子结点为2i+1)并用一维数组BT来表示。已知结点X、E和D在数组BT中的下标为分别为1、2、3,可推出结点G、K和H在数组BT中的下标分别为（　）。 ”相关问题

  • 第1题：

    用数组A[l..n]顺序存储完全二叉树的各结点,则当i>0,且i<=【 】时,结点A[i]的右子女是结点A[2i+1],否则结点A[i]没有右子女。


    正确答案：[(n-1)/2]
    [(n-1)/2] 解析：根据完全二叉树的定义及顺序存储结构的特点,可知答案为[(n-1)/2]。

  • 第2题：

    二叉树如右图所示,若进行顺序存储（即用一维数组元素存储该二叉树中的结点且通过下标反映结点间的关系，例如，对于下标为i的结点，其左孩子的下标为2i、右孩子的下标为2i+1），则该数组的大小至少为（ ）；若釆用三叉链表存储该二叉树（各个结 点包括结点的数据、父结点指针、左孩子指针、右孩子指针），则该链表的所有结点中空指针的数目为（ ）。

    A.6 B.10 C.12 D.15 A.6 B.8 C.12 D.14


    正确答案：D,B

  • 第3题：

    用数组A[1…n]顺序存储完全二叉树的各结点，则当i>0，且i<=__________时，结点A[i]的右子女是结点A[2i 1]，否则结点A[i]没有右子女。


    正确答案：
    (n-1)/2【解析】完全二叉树中除最下面一层外，各层都被结点充满了，每一层结点个数恰是上一层结点个数的2倍。因此，从一个结点的编号就可以推知它的双亲及左、右子女结点的编号。当i<=n/2时，结点i的左子女是结点2i，否则结点i没有左子女；当i<=(n-1)/2时，结点i的右子女是结点2i 1，否则结点i没有右子女；当i≠l时，结点i的双亲是结点[i/2]。

  • 第4题：

    某二叉树如图所示，若进行顺序存储（即用一维数组元素存储该二叉树中的结点且通过下标反映结点间的关系，例如，对于下标为i的结点，其左孩子的下标为2i、右孩子的下标为2i+1），则该数组的大小至少为（请作答此空）；若采用三叉链表存储该二叉树（各个结点包括结点的数据、父结点指针、左孩子指针、右孩子指针），则该链表的所有结点中空指针的数目为（ ）。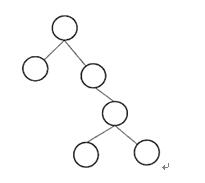

    A.6
    B.10
    C.12
    D.15

    答案：D
    解析：
    采用顺序存储结构存储二叉树时，一般的二叉树也必须按照完全二叉树的形式存储，需要填上一些不存在的"虚结点"。题中二叉树的高度为4，需要的存储空间为24-1=15，如下：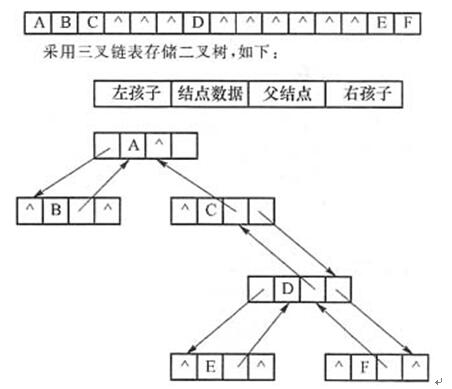

    可见，空指针的数目为8。

  • 第5题：

    对下图所示的二叉树进行顺序存储（根结点编号为1,对于编号为i的结点,其左孩子结点为2i,右孩子结点为2i+1）并用一维数组BT来表示,已知结点X、E和D在数组BT中的下标分别为1、2、3,可推出结点G、K和H在数组BT中的下分别为（ ）。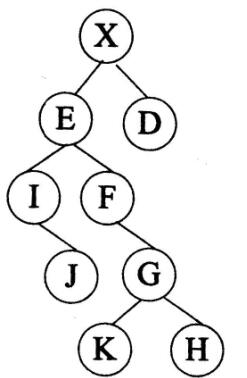

    A.10、11、12
    B.12、24、25
    C.11、12、13
    D.11、22、23

    答案：D
    解析：
    元素G为F的右子树,其下标为2F+1 ; F为元素E的右子树,其下标为2E+1, E的下标为2，因此G=2* (2*2+1) +1=11 ; K=2G=22 ; H=2G+1=23 ;

  • 第6题：

    按层次从上至下，每一层从左至右的顺序将二叉树的结点信息依次存放在数组元素BT[1]~BT[n]中，结点BT[i]如果存在右孩子，则该右孩子是（）


    正确答案:BT[2i+1]

  • 第7题：

    假定一棵二叉树顺序存储在一维数组a中，但让编号为1的结点存入a[0]元素中，让编号为2的结点存入a[1]元素中，其余类推，则编号为i结点的左孩子结点对应的存储位置为（），若编号为i结点的存储位置用j表示，则其左孩子结点对应的存储位置为（）。


    正确答案:2i-1；2j+1

  • 第8题：

    用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组A[1]~A[n]中，结点A[i]若有左子树，则左子树的根结点是（）。

    • A、A[2i-1]
    • B、A[2i+1]
    • C、A[i/2]
    • D、A[2i]

    正确答案:D

  • 第9题：

    用顺序存储的方法，将完全二叉树中所有结点按层逐个从左到右的顺序存放在一维数组R[1..N]中，若结点R[i]有右孩子，则其右孩子是（）。

    • A、R[2i-1]
    • B、R[2i+1]
    • C、R[2i]
    • D、R[2/i]

    正确答案:B

  • 第10题：

    填空题
    假定一棵二叉树顺序存储在一维数组a中，但让编号为1的结点存入a[0]元素中，让编号为2的结点存入a[1]元素中，其余类推，则编号为i结点的左孩子结点对应的存储位置为（），若编号为i结点的存储位置用j表示，则其左孩子结点对应的存储位置为（）。

    正确答案： 2i-1,2j+1
    解析： 暂无解析

  • 第11题：

    单选题
    用顺序存储的方法，将完全二叉树中所有结点按层逐个从左到右的顺序存放在一维数组R[1..N]中，若结点R[i]有右孩子，则其右孩子是（）。
    A

    R[2i-1]

    B

    R[2i+1]

    C

    R[2i]

    D

    R[2/i]


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组中R[1..n]，结点R[i]若有左孩子，其左孩子的编号为结点（）。
    A

     R[2i+1]

    B

     R[2i]

    C

     R[i/2]

    D

     R[2i-1]


    正确答案： C
    解析： 暂无解析

  • 第13题：

    若对一棵有n个结点的完全二叉树的结点按层自上而下、自左至右编号，则对任意结点i(1≤i≤n)，有( )。

    Ⅰ．若2i＞n，则结点i无左孩子

    Ⅱ若2i+1＞n，则结点无右孩子

    Ⅲ．若结点i有左孩子，则其左孩子编号为2i

    Ⅳ.若i＞1，则其双亲结点编号为{i/2}

    A．Ⅱ和Ⅲ

    B．Ⅰ和Ⅱ

    C．Ⅲ和Ⅳ

    D．全都是


    正确答案：D
    解析：通过二叉树的基本性质可以得到以上结论。

  • 第14题：

    对二叉树中的结点如下编号：树根结点编号为1，根的左孩子结点编号为2、右孩子结点编号为3，依此类推，对于编号为i的结点，其左孩子编号为2i、右孩子编号为2i+1。例如，下图所示二叉树中有6个结点，结点a、b、c、d、e、f的编号分别为1、2、3、5、7、11。那么，当结点数为n（n>0）的（ ）时，其最后一个结点编号为2i-1

    A.二叉树为满二叉树（即每层的结点数达到最大值）B.二叉树中每个内部结点都有两个孩子C.二叉树中每个内部结点都只有左孩子D.二叉树中每个内部结点都只有右孩子


    正确答案：C

  • 第15题：

    用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组A[1]～A[n]中，结点A[i]若有左子树，则左子树的根结点是()。

    A.A[i/2]
    B.A[2i]
    C.A[2i-1]
    D.A[2i+1]

    答案：B
    解析：
    据二叉树的性质5，对完全二叉树从上到下、从左至右给结点编号，若编号为2i的结点存在，则i的左子树一定是A[2i]。

  • 第16题：

    某二叉树如图所示，若进行顺序存储(即用一维数组元素存储该二叉树中的结点且通过下标反映结点间的关系，例如，对于下标为i的结点，其左孩子的下标为2i、右孩子的下标为2i+1)，则该数组的大小至少为（58）；若采用三叉链表存储该二叉树(各个结点包括结点的数据、父结点指针、左孩子指针、右孩子指针)，则该链表的所有结点中空指针的数目为（59）。

    A.6
    B.8
    C.12
    D.14

    答案：B
    解析：
    采用顺序存储结构存储二叉树时，一般的二叉树也必须按照完全二叉树的形式存储，需要填上一些不存在的“虚结点”。题中二叉树的高度为4，需要的存储空间为24-1=15，如下：可见，空指针的数目为8。

  • 第17题：

    对下面的二叉树进行顺序存储（用数组 MEM 表示）,已知结点 A、B、C 在 MEM 中对应元素的 下标分别为 1、2、3,那么结点 D、E、F 对应的数组元素下标为（ ）。


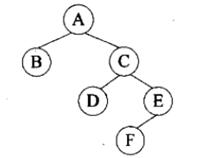    A.4、5、6
    B.4、7、10
    C.6、7、8
    D.6、7、14

    答案：D
    解析：
    以下列二叉树的顺序存储如下图：

  • 第18题：

    若对一棵二叉树从0开始进行结点编号，并按此编号把它顺序存储到一维数组a中，即编号为0的结点存储到a[0]中，其余类推，则a[i]元素的左孩子元素为（），右孩子元素为（），双亲元素（i>0）为（）。


    正确答案:A[2*i+1]；a[2*i+2]；a[i/2]

  • 第19题：

    在对二叉树进行顺序存储时，若下标为6的结点P既有双亲结点，又有左孩子结点和右孩子结点，则P的双亲结点的下标为（），左孩子结点的下标为（），右孩子结点的下标为（）


    正确答案:3；12；13

  • 第20题：

    一棵有n个结点的二叉树，按层次从上到下，同一层从左到右的顺序存储在一维数组A[n]中，则二叉树中第I个结点（I从1开始用上述方法编号）的右孩子在数组A中的位置是（）

    • A、A[2I]  （2I≤n）
    • B、A[2I+1]  （2I+1≤n）
    • C、A[i/2]
    • D、条件不充分，无法确定

    正确答案:D

  • 第21题：

    用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组中R[1..n]，结点R[i]若有左孩子，其左孩子的编号为结点（）。

    • A、 R[2i+1]
    • B、 R[2i]
    • C、 R[i/2]
    • D、 R[2i-1]

    正确答案:B

  • 第22题：

    填空题
    在对二叉树进行顺序存储时，若下标为6的结点P既有双亲结点，又有左孩子结点和右孩子结点，则P的双亲结点的下标为（），左孩子结点的下标为（），右孩子结点的下标为（）

    正确答案： 3,12,13
    解析： 由二叉树的性质⑤可知，若对任一完全二叉树上的所有结点按层从左向右编号，则结点编号之间的数值关系可以准确地反映结点之间的逻辑关系。因此，对于完全二叉树的顺序存储来说，采用的是“以编号为地址”的策略将结点存入作为顺序存储结构的一维数组，即将编号为i的结点存入一维数组的第i个单元。利用二叉树的性质⑤可求出结果

  • 第23题：

    填空题
    按层次从上至下，每一层从左至右的顺序将二叉树的结点信息依次存放在数组元素BT[1]~BT[n]中，结点BT[i]如果存在右孩子，则该右孩子是（）

    正确答案： BT[2i+1]
    解析： 暂无解析

相关内容