若用最小二乘法以净佣金率为因变量拟合得到的回归方程为Y=-0.852+0.O02X,说明( )。A.X与Y之间存在着负相关关系B.每人每月销售额X增加一元,则净佣金率Y就会提高0.002%C.每人每月销售额X增加一元,则净佣金率Y就会平均提高0.002%D.X与Y之间存在着显著的线性相关关系
题目
若用最小二乘法以净佣金率为因变量拟合得到的回归方程为Y=-0.852+0.O02X,说明( )。
A.X与Y之间存在着负相关关系
B.每人每月销售额X增加一元,则净佣金率Y就会提高0.002%
C.每人每月销售额X增加一元,则净佣金率Y就会平均提高0.002%
D.X与Y之间存在着显著的线性相关关系
相似考题
更多“若用最小二乘法以净佣金率为因变量拟合得到的回归方程为Y=-0.852+0.O02X,说明( )。 A.X与Y之间存 ”相关问题
-
第1题:
若用最小二乘法以利润率为因变量拟合得到的回归方程为Y=-0.852+0.002X,说明( )。
A.X与Y之间存在着负相关关系
B.每人每月销售额X增加一元,则利润率Y就会提高0.002%
C.每人每月销售额X增加一元,则利润率Y就会平均提高0.002%
D.X与Y之间存在着显著的线性相关关系
正确答案:C
解析:A项,在一元线性回归方程中,回归系数与相关系数r的符号一致,故X与Y之间存在着正相关关系;C项,回归系数表示自变量每变动一个单位量时,因变量的平均变化量,故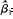 =0.002表示每人每月销售额X增加一元,则利润率Y就会平均提高0.002%;D项,F检验统计值未知,故无法判断X与Y之间是否存在着显著的线性相关关系。
=0.002表示每人每月销售额X增加一元,则利润率Y就会平均提高0.002%;D项,F检验统计值未知,故无法判断X与Y之间是否存在着显著的线性相关关系。
-
第2题:
现有八家百货公司,每个公司人均月销售额和利润率资料如表5—3所示。

用最小二乘法以利润率为因变量拟合直线回归方程,其最小二乘法的原理是使()。
 答案:B解析:
答案:B解析: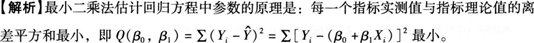
-
第3题:
下列关于多项式拟合函数a=polyfit(x,y,3)正确的是
A.x,y为长度相同的向量
B.其数学基础是最小二乘法曲线拟合原理
C.输出a为三维数组
D.拟合的三次多项式为a(1)*x.^3+a(2)*x.^2+a(3)*x
其数学基础是最小二乘法曲线拟合原理;x,y 为长度相同的向量 -
第4题:
现有八家百货公司,每个公司人均月销售额和利润率资料如表5—3所示。
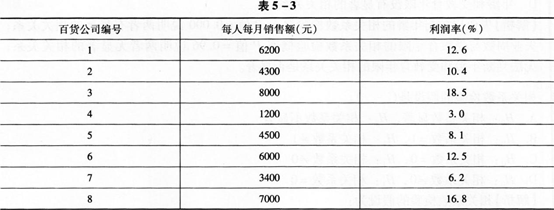
若用最小二乘法以利润率为因变量拟合得到的回归方程为Y=-0.852+0.002X,说明()。A.X与Y之间存在着负相关关系
B.每人每月销售额X增加一元,则利润Y就会提高0.002%
C.每人每月销售额X增加一元,则利润率y就会平均提高0.002%
D.X与Y之间存在着显著的线性相关关系答案:C解析:
-
第5题:
现有八家百货公司,每个公司人均月销售额和利润率资料如表5 -3所示。
表5 -3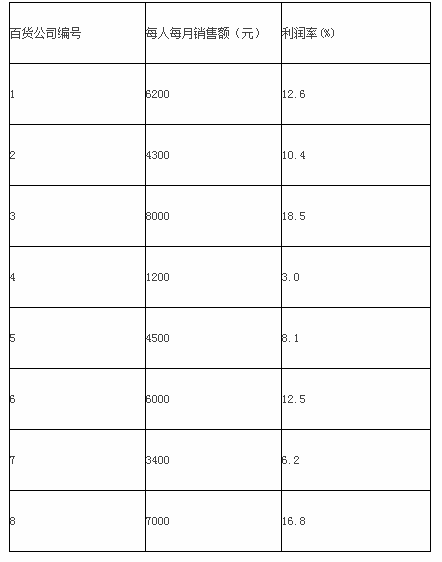
请根据上述资料进行计算和判断,从下列各题的备选答案中选出正确答案。
若用最小二乘法以利润率为因变量拟合得到的回归方程为Y=-0.852 +0. 002X,说明()。
A.X与Y之间存在着负相关关系
B.每人每月销售额X增加一元,则利润率Y就会提高0. 002%
C.每人每月销售额X增加一元,则利润率Y就会平均提高0. 002%
D.X与Y之间存在着显著的线性相关关系答案:C解析:A项,在一元线性回归方程中,回归系数β1与相关系数r的符号一致,故X与Y之间存在着正相关关系;c项,回归系数β1表示自变量每变动一个单位量时,因变量的平均变化量,故β1=0.002表示每人每月销售额X增加一元,则利润率Y就会平均提高0. 002%;D项,F检验统计值未知,故无法判断X与Y之间是否存在着显著的线性相关关系。
