甲乙两人独立进行射击,甲射中的概率为3/4,乙射中的概率为5/6,两个人是否命中相互没有影响,则至少有一人射中的概率为()。A:23/24 B:15/24 C:1/3 D:1/5
题目
甲乙两人独立进行射击,甲射中的概率为3/4,乙射中的概率为5/6,两个人是否命中相互没有影响,则至少有一人射中的概率为()。
A:23/24
B:15/24
C:1/3
D:1/5
B:15/24
C:1/3
D:1/5
相似考题
参考答案和解析
答案:A
解析:
此题较难,考查的是非互不相容事件概率的加法。首先可能出现两个人都射中的情况,即甲乙两人命中目标这两个事件属于非互不相容事件,设事件A表示甲命中目标,事件B表示乙命中目标,则至少有一人命中目标的概率为P(A+B)=P(A)+P(B)-P(AB)。其中P(A)=3/4,P(B)=5/6,又因为甲乙两人是否命中目标之间相互没有影响,即相互独立,所以P(AB)=P(A)*P(B)=3/4*5/6=15/24,因此P(A+B)=3/4+5/6-15/24=23/24。
更多“甲乙两人独立进行射击,甲射中的概率为3/4,乙射中的概率为5/6,两个人是否命中相互没有影响,则至少有一人射中的概率为()。”相关问题
-
第1题:
某人打靶击中的概率为3/4,如果直到射中靶为止,则射击次数为5的概率为()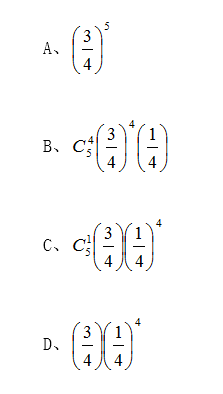 参考答案:D
参考答案:D
-
第2题:
某人连续向一目标独立射击(每次命中率都是3/4),一旦命中,则射击停止,设X 为射击的次数,那么射击3次停止射击的概率是: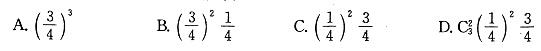 答案:C解析:
答案:C解析: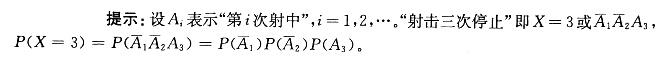
-
第3题:
甲乙两人独立地向同一目标各射击一次,命中率分别为0.8和0.6,现已知目标被击中,则它是甲射中的概率为:A.0.26
B.0.87
C.0.52
D.0.75答案:B解析:参考解析:提示:设“甲击中”为A,“乙击中”为B,A、B独立,目标被击中即甲、乙至少一人击中,求P(A│A+B)。

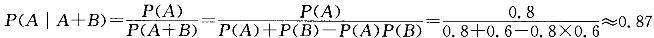
-
第4题:
甲、乙两人各自独立射击1次,甲射中目标的概率为0.8,乙射中目标的概率为0.9,则至少有一人射中目标的概率为()A.0.98
B.0.9
C.0.8
D.0.72答案:A解析:【考情点拨】本题考查了概率的知识点.
-
第5题:
甲、乙两人独立对同一目标进行射击,命中目标概率分别为60%和50%.
(1)甲、乙两人同时向目标射击,求目标被命中的概率;
(2)甲、乙两人任选一人,由此入射击,目标被击中,求是甲击中的概率.答案:解析:【解】(1)设A={甲击中目标},B={乙击中目标},C={击中目标},则C=A+B,
P(C)=P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)P(B)
=0.6+0.5-0.6×0.5=0.8.
(2)设A1={选中甲},A2={选中乙},B={目标被击中},则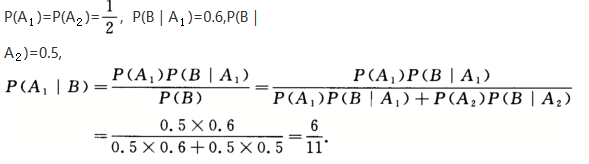
-
第6题:
甲、乙两人独立的对同一目标各射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率等于()。
- A、3/4
- B、3/5
- C、1/2
- D、3/7
- E、3/8
正确答案:A -
第7题:
在三次独立重复射击中,若至少有一次击中目标的概率为37/64,则每次射击击中目标的概率为()。
正确答案:1/4 -
第8题:
一射手对同一目标独立地进行4次射击,假设每次射击命中率相同,若至少命中1次的概率为80/81,则该射手的命中率p=()。
正确答案:2/3 -
第9题:
已知甲、乙两人击中目标的概率分别为0.9、0.8(两人互不影响),两人均射击一次,则两人中只有一人击中目标的概率为()。
- A、0.8
- B、0.18
- C、0.74
- D、0.26
正确答案:D -
第10题:
单选题甲乙两人独立地向同一目标各射击一次,命中率分别为0.8和0.6,现已知目标被击中,则它是甲射中的概率为:()A0.26
B0.87
C0.52
D0.75
正确答案: B解析: 暂无解析 -
第11题:
单选题每次射击时,甲击中目标的概率为0.8,乙击中目标的概率为0.6.甲、乙各自独立地向目标射击一次,则恰有一人击中的概率为( ).A0.44
B0.6
C0.8
D1
正确答案: A解析:
甲、乙各自独立地向目标射击一次,恰有一人击中,即甲击中或者乙击中,则有0.8×0.4+0.2×0.6=0.44. -
第12题:
问答题22.甲、乙两人独立地各向同一目标射击一次,其命中率分别为0.6和O.7,求目标被命中的概率.若已知目标被命中,求它是甲射中的概率.正确答案:解析: -
第13题:
甲和乙两个人进行射箭比赛,各射2支箭。已知甲每次射中的概率是60%,乙每次射中的概率是40%,若射中得1分,不中得0分,则两人得分相同的概率( )。A.小于10%
B.在20%到30%之间
C.在30%到40%之间
D.在50%到60%之间答案:C解析:得分相同,可能都是0分,都得1分,都得2分。
(1)都是 0 分的概率为:P0=(1-0.6)2 X (1-0. 4)2 =0. 0576。
(2)都得 1 分的概率为:P1=2X0. 6X(1-0. 6)X2X0. 4X(1-0. 4)=0. 2304。
(3)都得 2 分的概率为:P2=0. 62 X0. 42=0. 0576。
所以得分相同的概率为 0.0576+0. 2304 + 0. 0576 = 0. 3456,即34.56%。 -
第14题:
甲乙两人独立地向同一目标各射击一次,命中率分别为0. 8和0. 6,现已知目标被击中,则它是甲射中的概率为:A. 0. 26
B. 0. 87
C. 0. 52
D. 0. 75答案:B解析:提示:设“甲击中”为A,“乙击中”为B,A、B独立,目标被击中即甲、乙至少一人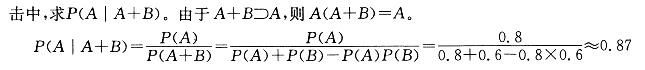
-
第15题:
某人打靶的命中率为0.6,现独立地射击5次,那么5次中有3次命中的概率为()
 答案:D解析:
答案:D解析: -
第16题:
甲、乙两人独立地向同一目标射击,甲、乙两人击中目标的概率分别为0.8,
0.5,两人各射击1次,求至少有1人击中目标的概率.答案:解析:
-
第17题:
战士甲进行射击训练,已知甲每次射击击中10环、9环、8环或8环以下的概率分别为0.2,0.3,0.5。现甲独立射击了2次,则甲至少有1次射中10环的概率是( )。A.0.24
B.0.36
C.0.2
D.0.32答案:B解析:一次射击中甲没射中10环的概率是0.8。则甲独立射击了2次,至少有1次射中10环的概率P=1-0.8×0.8=0.36。 -
第18题:
甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5.现已知目标被命中,则它是甲射中的概率是()
正确答案:6/11 -
第19题:
某人向同一目标独立重复射击,每次射击命中目标的概率为p(0<p<1),则此人第4次射击恰好第2次命中目标的概率为()。
- A、3p(1-p)2
- B、6p(1-p)2
- C、3p2(1-p)2
- D、6p2(1-p)2
正确答案:C -
第20题:
甲乙两人下棋,甲胜的概率为0.6,乙胜的概率为0.4,设A为甲胜,B为乙胜,则甲胜乙输的概率为()
- A、0.6∞0.6
- B、0.6-0.6∞0.4
- C、0.6-0.4
- D、0.6
正确答案:D -
第21题:
问答题41.某射手命中率为.他独立地向目标射击4次,则至少命中一次的概率为正确答案:解析: -
第22题:
单选题甲、乙两射手各进行一次射击,甲射中目标的概率为0.6,乙射中目标的概率为0.5,则至少有一人射目标的概率是()。A0.30
B0.50
C0.80
D其它
正确答案: D解析: 暂无解析 -
第23题:
单选题甲、乙两人独立的对同一目标各射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率等于()。A3/4
B3/5
C1/2
D3/7
E3/8
正确答案: B解析: 暂无解析
