方程是( )。A、一阶线性非齐次微分方程B、齐次方程C、可分离变量的微分方程D、二阶微分方程

题目
方程是( )。

A、一阶线性非齐次微分方程

B、齐次方程

C、可分离变量的微分方程

D、二阶微分方程

相似考题

1.线性时不变连续系统的数学模型是()。A.线性微分方程B.微分方程C.线性常系数微分方程D.常系数微分方程

2.若二阶常系数线性齐次微分方程y"+ay'+by=0的通解为y=(C1+C2x)e^x，则非齐次方程y"+ay'+by=x满足条件y(0)=2，y'(0)=0的解为y=________.

3.已知是某二阶常系数非齐次线性微分方程的3个解，则该方程的通解为y=________.

4.下列（　　）是可分离变量的微分方程．

参考答案和解析
正确答案:C
更多“方程是( )。 A、一阶线性非齐次微分方程B、齐次方程C、可分离变量的微分方程D、二阶微分方程”相关问题

  • 第1题：

    微分方程：ydx+（y2x-ey）dy=0是下述哪种方程？

    A.可分离变量方程
    B.—阶线性的微分方程
    C.全微分方程
    D.齐次方程

    答案：B
    解析：
    提示：方程可化为x'+p（y）x=Q（y）的形式。

  • 第2题：

    3阶常系数线性齐次微分方程的通解为y=________


    答案：
    解析：

  • 第3题：

    微分方程ydx+(y2x-ey)dy=0是( )方程。

    A.可分离变量
    B.一阶线性的微分
    C.全微分
    D.齐次

    答案：B
    解析：
    方程可化为x'+p(y)x=θ(y)的形式

  • 第4题：

    描述转子受扰运动的方程是（ ）。

    A.线性微分方程
    B.非线性微分方程
    C.代数方程
    D.变系数微分方程

    答案：B
    解析：

  • 第5题：

    以.为通解的二阶线性常系数齐次微分方程为_____


    答案：
    解析：
    所给问题为求解微分方程的反问题．常见的求解方法有两种：解法1先由通解写出二阶线性常系数齐次微分方程的特解，再由此写出方程的特征根r1，
    r2，第三步写出特征方程(r-r1)(r-r2)=0，再依此写出相应的微分方程；
    解法2由所给方程的通解，利用微分法消去任意常数，得出微分方程．这里只利用解法1求解．由于二阶线性常系数齐次微分方程的通解为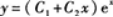，由其解的结构定理可知方程有两个特解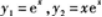：，从而知道特征方程的二重根r=1．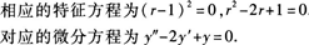

  • 第6题：

    二阶常系数齐次微分方程y″-4y′+4y=0的通解为_____．


    答案：
    解析：

  • 第7题：

    微分方程ydx+（y2x-ey）dy=0是下述哪种方程（）？

    • A、可分离变量方程
    • B、一阶线性的微分方程
    • C、全微分方程
    • D、齐次方程

    正确答案:B

  • 第8题：

    线性常系数微分方程表示的系统，方程的齐次解称为自由响应。


    正确答案:正确

  • 第9题：

    方程中出现的未知函数及其各阶导数都是一次幂形式的微分方程称为线性微分方程。


    正确答案:正确

  • 第10题：

    单选题
    若在常微分方程中出现的未知函数极其各阶导数都是一次幂形式，则称方程是（）。
    A

    一阶方程

    B

    齐次方程

    C

    线性方程

    D

    恰当方程


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    微分方程ydx+（y2x-ey）dy=0是下述哪种方程（）？
    A

    可分离变量方程

    B

    一阶线性的微分方程

    C

    全微分方程

    D

    齐次方程


    正确答案： B
    解析： 方程可化为x′+P（y）x=Q（y）的形式。

  • 第12题：

    单选题
    A

    齐次微分方程

    B

    可分离变量的微分方程

    C

    一阶线性微分方程

    D

    二阶微分微分方程


    正确答案： B
    解析：

  • 第13题：

    以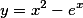和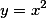为特解得一阶非齐次线性微分方程为


    答案：
    解析：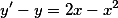

  • 第14题：

    设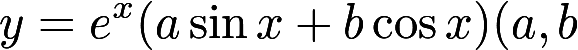 为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为


    答案：
    解析：

  • 第15题：

    微分方程



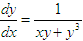
    是（　　）。

    A、 齐次微分方程
    B、 可分离变量的微分方程
    C、 一阶线性微分方程
    D、 二阶微分方程

    答案：C
    解析：

  • 第16题：

    下列微分方程中，可分离的变量方程是《》（ ）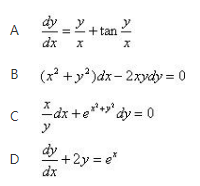


    答案：C
    解析：

  • 第17题：

    二阶线性常系数齐次微分方程y″+2y=0的通解为____．


    答案：
    解析：

  • 第18题：

    若在常微分方程中出现的未知函数极其各阶导数都是一次幂形式，则称方程是（）。

    • A、一阶方程
    • B、齐次方程
    • C、线性方程
    • D、恰当方程

    正确答案:C

  • 第19题：

    连续线性时不变系统的数学模型是（）

    • A、 线性微分方程
    • B、 微分方程
    • C、 线性常系数微分方程
    • D、 常系数微分方程

    正确答案:C

  • 第20题：

    线性常系数微分方程表示的系统，方程的齐次解称之自由响应，特解称之强迫响应。


    正确答案:正确

  • 第21题：

    描述转子受扰运动的方程是（）

    • A、线性微分方程
    • B、非线性微分方程
    • C、代数方程
    • D、变系数微分方程

    正确答案:B

  • 第22题：

    填空题
    若二阶常系数线性齐次微分方程y″＋ay′＋by＝0的通解为y＝（C1＋C2x）ex，则非齐次方程y″＋ay′＋by＝x满足条件y（0）＝2，y′（0）＝0的解为y＝____。

    正确答案： -xex+x+2
    解析：
    由题意可知，r＝1是已知齐次方程对应的特征方程的二重根，则该特征方程为（r－1）2＝r2－2r＋1＝0，齐次方程为y″－2y′＋y＝0设y*＝Ax＋B为已知非齐次方程y″－2y′＋y＝x的特解，代入y″－2y′＋y＝x得0－2A＋Ax＋B＝x，则A＝1，B＝2A＝2。故已知非齐次方程的通解为y＝（C1＋C2x）ex＋x＋2。又y（0）＝2，y′（0）＝0，代入以上通解得C1＝0，C2＝－1。故所求方程特解为y＝－xex＋x＋2。

  • 第23题：

    填空题
    设y1＝3＋x2，y2＝3＋x2＋e－x是某二阶线性非齐次微分方程的两个特解，且相应的齐次方程有一个解为y3＝x，则该方程的通解为____。

    正确答案： y=3+x2+c1x+c2e-x
    解析：
    由解的叠加原理可知，y2－y1＝e－x是原方程对应齐次方程的一个特解，可知该特解与题中给出的y3＝x线性无关，则原方程的通解为y＝3＋x2＋c1x＋c2e－x。

相关内容