二叉树指()。A.是四叉树的一种特例B.其表达中的结点分两类C.每个结点对应具有相同特性的像素组成的长方阵D.其表达图像所需的结点数总比四叉树所需的结点数少

题目
二叉树指()。

A.是四叉树的一种特例

B.其表达中的结点分两类

C.每个结点对应具有相同特性的像素组成的长方阵

D.其表达图像所需的结点数总比四叉树所需的结点数少

相似考题

1.遍历二叉树是指按照一定的规律走遍二叉树的每个结点,每个结点可能被访问多次。()此题为判断题(对，错)。

2.计算二叉树最大的宽度(二叉树的最大宽度是指二叉树所有层中结点个数的最大值)。

3.最优二叉树(或哈夫曼树)是指权值为 W1， W2，。。。，Wn 的 n 个叶结点的二叉树中带权路径长度最小的二叉树。（ ）是哈夫曼树(叶结点中的数字为其权值)。A.B.C.D.

4.下面是对二叉树的叙述，其中错误的是 （ ）A．二叉树的遍历是指不重复地访问二叉树中的所有结点B．二叉树的遍历允许重复地访问二叉树中的个别结点C．在遍历二叉树的过程中，一般先遍历左子树，然后再遍历右子树D．在先左后右的原则下，根据访问根结点的次序，二叉树的遍历可以分为三种：前序遍历、中序遍历、后序遍历

参考答案和解析
参考答案：A
更多“二叉树指()。 ”相关问题

  • 第1题：

    最优二叉树(或哈夫曼树)是指权值为w1，w2，…，wn的n个叶结点的二叉树中带权路径长度最小的二叉树。( )是哈夫曼树(叶结点中的数字为其权值)。



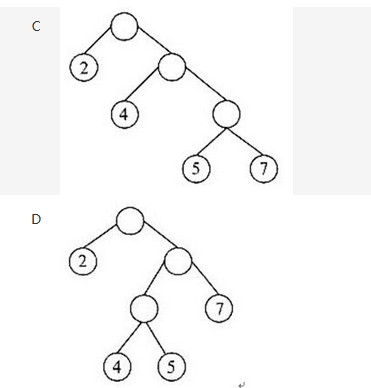    答案：A
    解析：
    本题考查数据结构基础知识。
    哈夫曼树又称为最优二叉树，是一类带权路径长度最短的树。
    树的带权路径长度(WPL)为树中所有叶子结点的带权路径长度之和，记为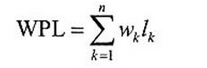

    其中n为带权叶子结点数目，wk为叶子结点的权值，lk为根到叶子结点的路径长度。
    选项A所示二叉树的WPL=(2+4)*3+5*2+7*1=35
    选项B所示二叉树的WPL=(2+4+5+7)*2=36
    选项C所示二叉树的WPL=(5+7)*3+4*2+2*1=46
    选项D所示二叉树的WPL=(4+5)*3+7*2+2*1=43

  • 第2题：

    二叉树的类型包括满二叉树和完全二叉树，关于他们的说法以下正确的是（）？

    A．满二叉树是指除了叶子结点外，树中每个结点都有两个左右子树。

    B．满二叉树的高度如果为h，则树的结点个数为2^(h)-1

    C．完全二叉树高度为h，所含结点个数为2^(h)-1

    D．完全二叉树结点编号方式可以和同样高度的满二叉树一样，从左到右，从上到下的顺序一一对应


    对

  • 第3题：

    假设二叉树中每个节点值为单个字符，采用二叉链存储结构存储。设计一个算法，求二叉树b的宽度（二叉树b的宽度是指其中所有层的节点个数的最大值）。


    intlog2(int x) // 求以2为底的x的对数 { int i=0; while (x!=1) { i++; x=x/2; } return i; } intLevel(SqBTree t ,int n,int i) //输出编号为i的节点的层次 { if (i<1 || i>n) return 0; else return log2(i)+1; }

  • 第4题：

    某二叉树的先序遍历序列为c a b f e d g,中序遍历序列为a b c d e f g,则该二叉树是（ ）。

    A.完全二叉树
    B.最优二叉树
    C.平衡二叉树
    D.满二叉树

    答案：C
    解析：
    本题考查数据结构基础知识。二叉树的遍历主要有四种：前序遍历（先根遍历、先序遍历）：遵循“根-左-右”的递归遍历思想，根一定是当前子二叉树先序遍历序列的第一个元素；中序遍历（中根遍历）：遵循“左-根-右”的递归遍历思想，根位于是当前子二叉树中序遍历序列的中部位置，左边是当前根的左二叉树，右边是当前根的右二叉树；后序遍历（后根遍历）：遵循“左-右-根”的递归遍历思想，根一定是遍历序列的最后一个元素；层次遍历：遵循从上到下，直左而右的遍历思想，根一定是遍历序列的第一个元素。根据题意，本二叉树为：



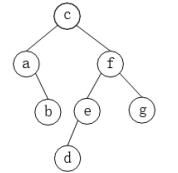
    平衡二叉树或者是一棵空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。本题的二叉树满足平衡二叉树的特点要求，故本题选择C选项

  • 第5题：

    根据先序序列ABDEC和中序序列BDEAC确定对应的二叉树，该二叉树（A ）。

    A．是完全二叉树但不是满二叉树

    B．不是完全二叉树

    C．是满二叉树

    D．不能确定


    是完全二叉树但不是满二叉树

  • 第6题：

    下列判断中，（）个是正确的。

    A．二叉树中不存在度大于2的结点

    B．对二叉树周游是指先根、中根和后根周游中的一种

    C．完全二叉树中，任何一个结点的度或者为0或者为2

    D．构造线索二叉树是为了方便找到每个结点的父结点


    CC。【解析】根据二叉树的性质，在任意二叉树中，度为0的结点(即叶子结点)总是比度为2的结点多一个。

相关内容