按行优先顺序存睹下三角矩阵的非零元素,则计算非零元素aij(1≤j≤i≤n)的地址的公式为A.LOC(aij)=LOC(a11)+i×(i+1)/2+jB.LOC(aij)=LOC(a11)+i×(i+1)/2+(j-1)C.LOC(aij)=LOC(a11)+i×(i-1)/2+jD.LOC(aij)=LOC(a11)+i×(i-1)/2+(j-1)
题目
按行优先顺序存睹下三角矩阵的非零元素,则计算非零元素aij(1≤j≤i≤n)的地址的公式为
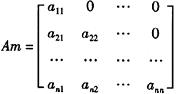
A.LOC(aij)=LOC(a11)+i×(i+1)/2+j
B.LOC(aij)=LOC(a11)+i×(i+1)/2+(j-1)
C.LOC(aij)=LOC(a11)+i×(i-1)/2+j
D.LOC(aij)=LOC(a11)+i×(i-1)/2+(j-1)
相似考题
更多“ 按行优先顺序存睹下三角矩阵的非零元素,则计算非零元素aij(1≤j≤i≤n)的地址的公式为A.LOC(aij)=LOC(a11)+i×(i+1)/2+jB.LOC(aij)=LOC(a11)+i×(i+1)/2+”相关问题
-
第1题:
按行优先顺序存储下三角矩阵的非零元素,则计算非零元素aij(1≤j≤i≤n)的地址的公式为( )。 A.LOC(aij)=LOC(a11)+i×(i+1)/2+j B.LOC(aij)=LOC(all)+i×(i+1)/2+(j-1) C.LOC(aij)=LOC(all)+i×(i-1)/2+(j+1) D.LOC(aij)=LOC(all)+i×(i-1)/2+(j-1)
正确答案:D
LOC(aij)=LOC(all)+i×(i-1)/2+(j-1) -
第2题:
按行优先顺序存下三角矩阵的非零元素,则计算非元素aij(1≤j≤i≤n)的地址的公式为

A.LOC(aij)=LOC(a11)+i×(i+1)/2+j
B.LOC(aij)=LOC(a11)+i×(i+1)/2+(j-1)
C.LOC(aij)=LOC(a11)+i×(i-1)/2+j
D.LOC(aij)=LOC(a11)+i×(i-1)/2+(j-1)
正确答案:D
解析:通过运算可以得出结论D正确。 -
第3题:
按行优先顺序存储下三角矩阵

的非零元素,则计算非零元素aij(1<jsi<n)的地址的公式为( )。
A)LOC(aij)=LOC(a11)+i×(i+1)/2+j
B)LOC(aij)=LOC(a11)+i×(i+1)/2+(j-1)
C)LOC(aij)=LOC(a11)+i×(i-1)/2+j
D)LOC(aij)=LOC(a11)+i×(i-1)/2+(j-1)
正确答案:D
非零元素aij在矩阵中处在第i行第j列,在按行优先顺序存储时,应先存储前i-1行的非零元素和同一行的前j-1个元素。如果a11的存储地址为LOC(a11),则aij的存储地址为LOC(aij)=LOC(a11)+i×(i-1)/2+(j一1)。 -
第4题:
按行优先顺序存储下三角矩阵的非零元素,非零元素aij(1≤i≤j≤n)地址计算公式是 ______。

A.LOC(aij)=LOC(a11)+i×(i+1)/2+i
B.LOC(aij)=LOC(a11)+i×(i+1)/2+(i-1)
C.LOC(aij)=LOC(a11)+i×(i-1)/2+i
D.LOC(aij)=LOC(a11)+i×(i-1)/2+(i-1)
正确答案:D
解析:具有大量0元素的矩阵称做稀疏矩阵。若非0元素的分布有规律,则可以用顺序方法存储非0元素,仍可以用公式计算数组元素的地址。如下三角矩阵,其非零元素的地址可用下式计算:LOC(aij)=LOC(a11)+i ×(i-1)/2+(j-1),1≤i≤j≤n -
第5题:
按行优先顺序存储下三角矩阵的非零元素,则计算非零元素aij(1≤j≤i≤n)的地址的公式为Am=[*]
A.LOC(aij)=LOC(a11)+i×(i+1)/2+i
B.LOC(aij)=LOC(a11)+i×(i+1)/2+(i-1)
C.LOC(aij)=LOC(a11)+i×(i-1)/2+i
D.IOC(aij)=LOC(a11)+i×(i-1)/2+(i-1)
正确答案:D
解析:通过运算可以得出结论D正确。
