在多元回归分析中,为避免增加自变量而高估R的平方,统计学家提出调整的多重判定系数R的平方,记为()。A、B、C、D、

题目
在多元回归分析中,为避免增加自变量而高估R的平方,统计学家提出调整的多重判定系数R的平方,记为()。

A、

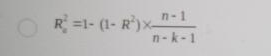
B、

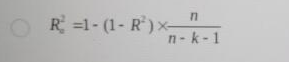
C、

D、

相似考题

1.下列关于判定系数R2的说法，正确的有( )。A.残差平方和越小，R2越小B.残差平方和越小，R2越大C.R2=1时，模型与样本观测值完全拟合D.R2越接近于1，模型的拟合程度越高E.可决系数的取值范围为0≤R2≤1

2.41、已知回归平方和SSR=4854，残差平方和SSE=146，则判定系数R^2=A．97.08%B．2.92%C．3.01%D．33.25%

3.在方差分析中，用于度量自变量与因变量之间关系强度的统计量是R²，其计算方法为（）。A．R²=组间平方和/组内平方和B．R²=组间平方和/总平方和C．R²=组间方差/组内方差D．R²=组内平方和/总平方和

4.下列关于判定系数R2的说法，正确的有（）。A.残差平方和越小，R2越小 B.残差平方和越小，R2越大 C.R2=1时，模型与样本观测值完全拟合 D.R2越接近于1，模型的拟合程度越高 E.可决系数的取值范围为0≤R2≤1

更多“在多元回归分析中,为避免增加自变量而高估R的平方,统计学家提出调整的多重判定系数R的平方,记为()。 ”相关问题

  • 第1题：

    关于回归分析中判定系数R²，错误的说法是__________

    A．在一元线性回归中，判定系数等于因变量与自变量样本相关系数的平方

    B．R²的值反映了在因变量的变动中由自变量变动所解释的百分比

    C．只要R²足够大，回归方程就通过检验

    D．取值区间为0≤R²≤1


    回归分析的目的就是计算回归方程的系数，使得样本的输入和输出之间的关系能够合理拟合。

  • 第2题：

    在一元线性回归模型中，已知观测值的个数为50，回归平方和为39860，总离差平方和为48860，则自变量和因变量之间的样本相关系数r可能是（）。

    A．0.90

    B．1

    C．-1

    D．0


    C

  • 第3题：

    17、在方差分析中，用于度量自变量与因变量之间关系强度的统计量是R²，其计算方法为（）。

    A．R²=组间平方和/组内平方和

    B．R²=组间平方和/总平方和

    C．R²=组间方差/组内方差

    D．R²=组内平方和/总平方和


    B

  • 第4题：

    已知回归平方和SSR=4854，残差平方和SSE=146，则判定系数R^2=

    A．97.08%

    B．2.92%

    C．3.01%

    D．33.25%


    97.08%

  • 第5题：

    多重相关系数的解释（）

    A．回归平方和占总平方和的比例

    B．计算公式为

    C．因变量取值的变差中，能被估计的多元回归方程所解释的比例

    D．在因变量取值的变差中，能被自变量解释的比例


    回归平方和占总平方和的比例;计算公式为;因变量取值的变差中，能被估计的多元回归方程所解释的比例;在因变量取值的变差中，能被自变量解释的比例

相关内容