一段长为36m的篱笆围成一个矩形菜园,问这个矩形的长和宽各为多少时,菜园的面积最大,最大面积为()A.90B.81C.72D.80
题目
一段长为36m的篱笆围成一个矩形菜园,问这个矩形的长和宽各为多少时,菜园的面积最大,最大面积为()
A.90
B.81
C.72
D.80
相似考题
参考答案和解析
9,9
更多“一段长为36m的篱笆围成一个矩形菜园,问这个矩形的长和宽各为多少时,菜园的面积最大,最大面积为()”相关问题
-
第1题:
某农民原有材料可建50米的篱笆,打算利用已有的一面墙沿墙建4间同样大小的矩形鹅舍,那么,鹅舍的最大面积为( )平方米。
A.25
B.28.25
C.31.25
D.35
正确答案:C
[答案] C。解析:设每间鹅舍的长为x米,宽为y米。那么有4x+5y=50,两数之和为定数,要使乘积4x×5y=20xy最大,只有4x=5y=25,则x=6.25米,y=5米,故每间鹅舍的最大面积为6.25×5=31.25平方米。
-
第2题:
用篱笆围成一个面积为625平方米的正方形菜园,现用总长度为100米的篱笆将菜园分隔成面积相同的小菜园,问最多能分成多少个小菜园:
A5
B8
C9
D12答案:C解析: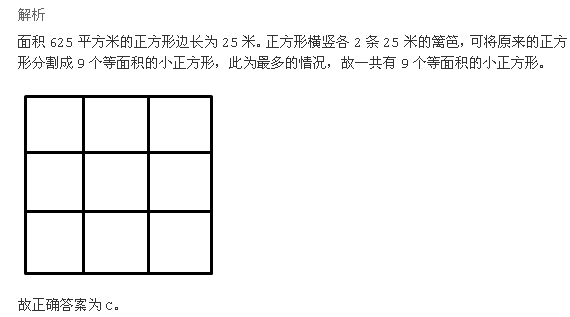
-
第3题:
某市为了解决停车难问题,在如下图所示的一段长55米的路宽开辟斜列式停车位,每个车位为长6米、宽2.6米的矩形,矩形的宽与路边成30°角,则在这个路段最多可以划出多少个这样的停车位?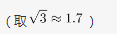 A.16
A.16
B.17
C.18
D.19答案:B解析:
-
第4题:
某农家要建造一个新的矩形鸡圈,如图所示,该鸡圈一面靠围墙,另外三面共使用了200米长的铁丝网,问如果想让鸡圈的面积最大,鸡圈的长和宽比值应为多少?
 A.1∶1
A.1∶1
B.2∶1
C.3∶2
D.7∶3答案:B解析:第一步,本题考查几何问题,属于平面几何类。
第二步,根据题意,设长为x米,宽为y米,则x+2y=200。长方形的面积为xy,根据均值不等式定理,当且仅当x=2y时
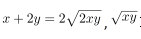
取得最大值,此时长方形的面积最大。
第三步,当x=2y时,所以鸡圈的长和宽的比值为2︰1。
因此,选择B选项。
拓展
均值不等式定理:对非负实数a、b,有a2+b2≥2ab(当且仅当a=b时取“=”号)。 -
第5题:
某矩形场地,长500米,宽200米,其面积为( )亩。A.50
B.100
C.150
D.200答案:C解析:总面积 100000 平方米合约 150 亩。 -
第6题:
已知一矩形面积为239,矩形四个角为R3的圆角,矩形长为32,求其宽度()
- A、7.7
- B、7.47
- C、7.5
- D、不存在
正确答案:A -
第7题:
用12米长的篱笆围成一个一边是墙的矩形鸡场,要使鸡场的面积最大,矩形的面积应是()
- A、3
- B、6
- C、8
- D、18
正确答案:D -
第8题:
发生对称弯曲的矩形截面梁,最大剪力为Fsmax,横截面面积为A,则最大切应力τmax(),最大切应力位于()。
正确答案:τmax=3Fsmax/2A;最大剪力所在截面的中性轴上 -
第9题:
问答题矩形基坑底面积为28m×36m,深4m,边坡系数为0.5,试计算其土方量?正确答案: ∵H∶B=1∶0.5
H.4m
∴B=2m
F1=28×36=1008
F2=(28+4)×(36+4)=1280
F0=(28+2)×(36+2)=1140
V=H/6(F1+4F0+F2)=4/6(1008+4×1140+1280)=4565.33m3解析: 暂无解析 -
第10题:
单选题被积函数是常数1而被积区域是一个矩形时,二重积分的值()。A是这个矩形线的周长
B是以这个矩形为底面的锥体体积
C是这个矩形的面积
D是以这个矩形为底面的柱体表面积
正确答案: B解析: 暂无解析 -
第11题:
单选题已知一矩形面积为239,矩形四个角为R3的圆角,矩形长为32,求其宽度()A7.7
B7.47
C7.5
D不存在
正确答案: A解析: 暂无解析 -
第12题:
问答题一矩形基础,宽为3m,长为4m,在长边方向作用一偏心荷载F+G=1200kN。偏心距为多少时,基底不会出现拉应力?试问当Pmin=0时,最大压力为多少?正确答案: e=0.67 Pmax=200kpa解析: 暂无解析 -
第13题:
用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成的最大的一个长方形的面积是多少平方厘米?( )A. 16
B. 15
C. 12
D. 9答案:B解析:设长方形的长为a,宽为b,则这个问题就是求已知a+b=8、且a≠b时,axb的最大值。为了便于观察,我们分析如下:
8 = 1 + 7→1X7=7;8 = 2 + 6→2X6 = 12;
8 = 3 + 5→3 X5=15;8 = 4 + 4→4 X 4 = 16;
8 = 5 + 3→5X3=15;8 = 6 + 2 → 6X2 = 12;
8 = 7 + 1→ 7X1=7。
我们发现当a从小到大取值,而b从大到小取值时,a与b的积呈现这样一个变化趋势:就是先由小到大,再由大到小,中间是最大的,也就是a与b取的数越接近,它们的乘积就越大。当a = b时,aXb的值最大。由此,得出一条规律:
如果a+b—定,只有当a =b时,a与b的乘积才最大。
由上面的讨论可知,在a +b=8,且a≠b中,当a=3,b= 5时,aXb的最大值是:3X5 = 15。 所以,所围成的最大的一个长方形的面积是15平方厘米。故本题正确答案为B。 -
第14题:
张家和李家都使用90米的篱笆围成了长方形的菜园,已知李家的长方形菜园的长边比张家短5米,但是菜园面积却比张家大50平方米,则李家的长方形菜园面积为( )。A. 550平方米
B. 500平方米
C. 450平方米
D. 400平方米答案:B解析:缺少的量为张家和李家菜园的具体长宽,可用方程法。设李家菜园长边为x米,则其短边长为45-x米;张家菜园长边为x+5米,其短边长为40-x,根据题意:x(45-x)-(x+5)×(40-x)=50,可解得x=25,李家菜园面积为x(45-x)=25×20=500。故本题答案为B选项。 -
第15题:
在美化城市活动中,某街道工作人员想借助如图所示的直角墙角,用28米长的篱笆围成一个矩形花园ABCD,篱笆只围AB、BC两边。图中P为一棵直径为1米的树,其与墙CD、AD的最短距离分别是14米和5米,若要将这棵树围在花园内,则花园的最大面积为多少平方米? A.187
A.187
B.192
C.195
D.196答案:C解析:第一步,本题考查几何问题,属于几何构造类,用最值理论解题。
第二步,四边形周长固定,越接近于正方形,面积越大,即让矩形ABCD的长与宽越接近越好。树到CD边的最短距离为垂线距离,是14米,树的直径为1米,那么矩形的长AD至少为14+1=15(米);树到AD边的最短距离为垂线距离,是5米,树的直径为1米,那么矩形的宽CD至少为5+1=6(米)。
第三步,长与宽越接近,面积越大,因为绳子的长度为28米,那么让长为15米,宽最大为13米,此时矩形面积最大,面积为15×13=195(平方米)。
因此,选择C选项。 -
第16题:
张家和李家都使用90米的篱笆围成了长方形的菜园,已知李家的长方形菜园的长边比张家短5米。但是菜园面积却比张家大50平方米,则李家的长方形菜园面积为多少?A.550平方米
B.500平方米
C.450平方米
D.400平方米答案:B解析:设李家菜园的长边为x,则短边为45-x;张家菜园的长为x+5,短边为40-x,根据题意列方程,x(45-x)-(x+5)(40-x)=50,解得x=25,则李家的长方形菜园面积为25×(45-25)=500平方米。 -
第17题:
在一个半径为R的圆内,要截出一个面积最大的矩形,问长宽各是多少?
正确答案: 设矩形的长宽各为a、b
则:a2+b2=(a-b)2+2ab=(2R)2
又:S矩形=a×b=[(2R)2-(a-b)2]/2
∴a、b最大为a:b=R
即当a=b=R时,矩形面积最大
长、宽分别为R时截出的矩形面积最大。 -
第18题:
矩形基坑底面积为28m×36m,深4m,边坡系数为0.5,试计算其土方量?
正确答案: ∵H∶B=1∶0.5
H.4m
∴B=2m
F1=28×36=1008
F2=(28+4)×(36+4)=1280
F0=(28+2)×(36+2)=1140
V=H/6(F1+4F0+F2)=4/6(1008+4×1140+1280)=4565.33m3 -
第19题:
一段长度相等的绳子,围成什么图形面积最大?
正确答案:围成圆形面积最大。 -
第20题:
某矩形场地,长500米,宽200米,其面积为()亩。
- A、50
- B、100
- C、150
- D、200
正确答案:C -
第21题:
单选题将四个完全相同的矩形(长是宽的3倍),用不同的方式拼成一个大矩形,设拼得的大矩形面积是四个小矩形的面积和,则大矩形周长的值只可能是( )。A1种
B2种
C3种
D4种
正确答案: B解析:
长:12、6、4,宽:1、2、3。 -
第22题:
问答题在一个半径为R的圆内,要截出一个面积最大的矩形,问长宽各是多少?正确答案: 设矩形的长宽各为a、b
则:a2+b2=(a-b)2+2ab=(2R)2
又:S矩形=a×b=[(2R)2-(a-b)2]/2
∴a、b最大为a:b=R
即当a=b=R时,矩形面积最大
长、宽分别为R时截出的矩形面积最大。解析: 暂无解析 -
第23题:
单选题用12米长的篱笆围成一个一边是墙的矩形鸡场,要使鸡场的面积最大,矩形的面积应是( )。A3
B6
C8
D18
正确答案: B解析:
设矩形的宽为x米,由篱笆一边是墙可知,长为(12-2x)米,则面积S=x(12-2x)=-2(x-3)2+18;当x=3米时,Smax=18平方米,即鸡场的最大面积为18平方米。 -
第24题:
单选题某矩形场地,长500米,宽200米,其面积为()亩。A50
B100
C150
D200
正确答案: A解析: 暂无解析
