【单选题】Nevile插值多项式中的P0,1（X)是（)。A．线性函数B．二次函数C．不确定D．常数

题目

【单选题】Nevile插值多项式中的P0,1（X)是（)。

A．线性函数

B．二次函数

C．不确定

D．常数

相似考题

1.拉格朗日插值法和牛顿插值法的共同缺点是:插值曲线在节点处不光滑、有尖点,而且插值多项式在节点处不可导。()

2.插值多项式余项Rn(x)与f(x)联系很紧。()

3.若在[a,b]上用Ln(x)近似f(x)，则其截断误差为Rn(x)=f(x)-Ln(x)，也称为插值多项式的()A、余项B、插值公式C、插值多项式D、以上都不对

4.所谓分段插值，就是选取分段多项式作为插值函数。()

更多“【单选题】Nevile插值多项式中的P0,1（X)是（)。”相关问题

  • 第1题：

    经过A(0,1),B(1,2),C(2,3)的插值多项式P(x)=()

    A、x

    B、x+1

    C、2x+1

    D、x^2+1


    参考答案：D

  • 第2题：

    多项式插值被认为是最好的逼近工具之一。()


    参考答案：√

  • 第3题：

    对于代数插值，插值多项式的次数随着节点个数的增加而升高。()


    参考答案：√

  • 第4题：

    设服从N(0,1)分布的随机变量X，其分布函数为φ(x)，如果φ(1)=0.84，则P|x|≤1的值是( )。



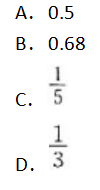    答案：B
    解析：
    X～N(0,1)，P{|x|≤1)=2Φ(1)-1=0.68

  • 第5题：

    两个本原多项式g（x）和f（x），令h（x）=g（x）f（x）记作Cs，若h（x）不是本原多项式，则存在p当满足什么条件时使得p|Cs（s=0，1…）成立？（）

    • A、p是奇数
    • B、p是偶数
    • C、p是合数
    • D、p是素数

    正确答案:D

  • 第6题：

    通过四个互异节点的插值多项式p（x），只要满足（），则p（x）是不超过二次的多项式。


    正确答案:满足三阶均差为0

  • 第7题：

    一维数据插值的函数yi=interp1（x，y，xi，’nearest’）表示（）。

    • A、线性插值
    • B、最近点插值
    • C、3次多项式插值
    • D、3次样条插值

    正确答案:B

  • 第8题：

    单选题
    f（x）（系数为an…a0）是一个次数n>0的本原多项式，q/p是有理根，那么可以得到f（x）=（px-q）g（x）成立，那么g（x）是什么多项式？（）
    A

    任意多项式

    B

    非本原多项式

    C

    本原多项式

    D

    无理数多项式


    正确答案： D
    解析： 暂无解析

  • 第9题：

    填空题
    通过四个互异节点的插值多项式p（x），只要满足（），则p（x）是不超过二次的多项式。

    正确答案： 满足三阶均差为0
    解析： 暂无解析

  • 第10题：

    单选题
    已知两点(2,4)、(4,6),利用插值多项式求点(3,x)中的x为（　）。
    A

    4.5

    B

    5.0

    C

    4.75

    D

    5.5


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    设fˊ（-1）=1，fˊ（0）=3，fˊ（2）=4，则抛物插值多项式中x2的系数为（）。
    A

    -0.5

    B

    0.5

    C

    2

    D

    -2


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    一维数据插值的函数yi=interp1（x，y，xi，’cubic’）表示（）。
    A

    线性插值

    B

    最近点插值

    C

    3次多项式插值

    D

    3次样条插值


    正确答案： A
    解析： 暂无解析

  • 第13题：

    通过四个互异节点的插值多项式p(x),只要满足(),则p(x)是不超过二次的多项式。

    A、一阶均差为0

    B、二阶均差为0

    C、三阶均差为0

    D、四阶均差为0


    参考答案：C

  • 第14题：

    依据3个样点(0，1)，(1，2)(2，3)，其插值多项式p(x)为()

    A、x

    B、x+1

    C、x-1

    D、x+2


    参考答案：B

  • 第15题：

    由于代数多项式的结构简单，数值计算和理论分析都很方便，实际上常取代数多项式作为插值函数，这就是所谓的()

    A、泰勒插值

    B、代数插值

    C、样条插值

    D、线性插值


    参考答案：B

  • 第16题：

    设fˊ（-1）=1，fˊ（0）=3，fˊ（2）=4，则抛物插值多项式中x2的系数为（）。

    • A、-0.5
    • B、0.5
    • C、2
    • D、-2

    正确答案:A

  • 第17题：

    给定插值点（xi，fi）（i=0，1，...，n）可分别构造Lagrange插值多项式和Newton插值多项式，它们是否相同？为什么？它们各有何优点？


    正确答案: 给定插值点后构造的Lagrange多项式为Ln（x）Newton插值多项式为Nn（x）它们形式不同但都满足条件Ln（xi）=fi，Nn（xi）=fi（i=0，1，...，n），于是Ln（xi）-Nn（xi）=0，i=0，1，...，n。它表明n次多项式[Ln（x）-Nn（x）]有n+1个零点，这与n次多项式只有n个零点矛盾，故Ln（x）=Nn（x）即Ln（x）与Nn（x）是相同的。Ln（x）是用基函数表达的，便于研究方法的稳定性和收敛性等理论研究和应用，但不便于计算，而Nn（x）每增加一个插值点就增加一项前面计算都有效，因此较适合于计算。

  • 第18题：

    设f（0）=0，f（1）=16，f（2）=46，则f[0，1]=（），f[0，1，2]=（），f（x）的二次牛顿插值多项式为（）。


    正确答案:16；7；0+16（x-0）+7（x-0）（x-1）

  • 第19题：

    单选题
    若p（x）是F（x）中次数大于0的不可约多项式，那么可以得到下列哪些结论？（）
    A

    只能有（p（x），f（x））=1

    B

    只能有（p（x）

    C

    （p（x），f（x））=1或者（p（x）

    D

    （p（x），f（x））=1或者（p（x）


    正确答案： D
    解析： 暂无解析

  • 第20题：

    填空题
    设f（0）=0，f（1）=16，f（2）=46，则f[0，1]=（），f[0，1，2]=（），f（x）的二次牛顿插值多项式为（）。

    正确答案： 16,7,0+16（x-0）+7（x-0）（x-1）
    解析： 暂无解析

  • 第21题：

    问答题
    给定插值点（xi，fi）（i=0，1，...，n）可分别构造Lagrange插值多项式和Newton插值多项式，它们是否相同？为什么？它们各有何优点？

    正确答案： 给定插值点后构造的Lagrange多项式为Ln（x）Newton插值多项式为Nn（x）它们形式不同但都满足条件Ln（xi）=fi，Nn（xi）=fi（i=0，1，...，n），于是Ln（xi）-Nn（xi）=0，i=0，1，...，n。它表明n次多项式[Ln（x）-Nn（x）]有n+1个零点，这与n次多项式只有n个零点矛盾，故Ln（x）=Nn（x）即Ln（x）与Nn（x）是相同的。Ln（x）是用基函数表达的，便于研究方法的稳定性和收敛性等理论研究和应用，但不便于计算，而Nn（x）每增加一个插值点就增加一项前面计算都有效，因此较适合于计算。
    解析： 暂无解析

  • 第22题：

    单选题
    仅能够用于节点等间距的插值多项式为（　）。
    A

    拉格朗日插值公式

    B

    牛顿插值公式

    C

    牛顿基本插值公式

    D

    三次样条插值公式


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    两个本原多项式g（x）和f（x），令h（x）=g（x）f（x）记作Cs，若h（x）不是本原多项式，则存在p当满足什么条件时使得p|Cs（s=0，1…）成立？（）
    A

    p是奇数

    B

    p是偶数

    C

    p是合数

    D

    p是素数


    正确答案： D
    解析： 暂无解析

  • 第24题：

    单选题
    经过点A(0,1),B(1,2),C(2,3)的插值多项式P(x)为（　）。
    A

    x

    B

    x+1

    C

    2x十1

    D

    五十1


    正确答案： B
    解析： 暂无解析

相关内容