所谓的n阶（n＞3）三对角矩阵（带状矩阵）是指非零元素只出现在矩阵的两条对角线上。（）

题目

所谓的n阶（n＞3）三对角矩阵（带状矩阵）是指非零元素只出现在矩阵的两条对角线上。（）

相似考题

1.可对角化的矩阵是____。A.实对称阵B.有n个相异特征值的n阶阵C.有n个线性无关的特征向量的n阶方阵

2.关于主对角线(从左上角到右下角)对称的矩阵为对称矩阵;如果一个矩阵中的各个元素取值为0或1，那么该矩阵为01矩阵，求大小为N*N的01对称矩阵的个数?()A.power(2,n);B.power(2,n*n/2);C.power(2,(n*n+n)/2);D.power(2,(n*n-n)/2);

3.以下程序用来建立一个10*10矩阵，该矩阵两条对角线上的元素为1，其余元素为0，请补充完该程序。该程序运行结果见下图。Private Sub Form_ click()Dim s(10, 10) As IntegerFor n = 1 To 10For m = 1 To 10If【 】Or【 】Thens (n, m) = 1Elses (n, m) = 0End IfNext mNext nFor n = 1 To 10For【 】。Picturel. Print Tab(m * 3); s(n, m)Next mPrintNext nEnd Sub

4.● 已知对称矩阵 An*n（Ai,j=Aj,i）的主对角线元素全部为0，若用一维数组B 仅存储矩阵 A 的下三角区域的所有元素（不包括主对角线元素），则数组 B的大小为（40）。（40）A.n(n-1)B.n2/2C.n(n-1)/2D.n(n+1)/2

更多“所谓的n阶（n＞3）三对角矩阵（带状矩阵）是指非零元素只出现在矩阵的两条对角线上。（）”相关问题

  • 第1题：

    反对称矩阵的主对角线上的元素和为0。()


    参考答案：正确

  • 第2题：

    若采用邻接矩阵法存储一个n个顶点的无向图，则该邻接矩阵是一个( )。

    A．上三解矩阵

    B．稀疏矩阵

    C．对角矩阵

    D．对称矩阵


    正确答案：D
    解析：在邻接矩阵来表示的图中，从一个点到另一个点的边，则相应位置上为1，否则为1，由于是无向图，点a到b存在边，那么点b到a也存在边，因此表示出来的邻接矩阵为对称矩阵。

  • 第3题：

    若将N阶对称矩阵A按照行序为主序方式将包括主对角线元素在内的下三角形的所有元素依次存放在一个一维数组B中，则该对称矩阵在B中占用了(40)—个数组元素。(40)

    A．N2

    B．N×(N-1)

    C．N×(N+1)/2

    D．N×(N-1)/2


    正确答案：C
    解析：因为N阶对称矩阵包括主对角线元素在内的下三角形的所有元素一共为N×(N+1)/2，因此应选择C。

  • 第4题：

    与n阶单位矩阵E相似的矩阵是

    A.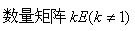
    B.对角矩阵D（主对角元素不为1）
    C.单位矩阵E
    D.任意n阶矩阵A


    答案：C
    解析：

  • 第5题：

    设N阶矩阵A与对角矩阵合同,则A是().

    A.可逆矩阵
    B.实对称矩阵
    C.正定矩阵
    D.正交矩阵

    答案：B
    解析：

  • 第6题：

    设有 n 阶三对角矩阵 A，即非零元素都位于主对角线以及与主对角线平行且紧邻的两条对角线上，现对该矩阵进行按行压缩存储，若其压储空间用数组 B 表示，A 的元素下标从 0开始，B 的元素下标从 1 开始。已知 A［0,0］存储在 B［1］，A［n－1，n－1］存储在 B［3n-2］，那么非零元素 A［i,j］（0≤ i＜n，0≤ j＜n，│i-j│≤1）存储在 B（ ）

    A.2i+j-1
    B.2i+j
    C.2i+j+1
    D.3i-j+1

    答案：C
    解析：

  • 第7题：

    设A为n阶非零矩阵,且存在自然数k,使得A^k=O.证明：A不可以对角化.


    答案：
    解析：

  • 第8题：

    设n阶矩阵A 满足，其中s≠t，证明A可对角化


    答案：
    解析：

  • 第9题：

    设有 n 阶三对角矩阵A,即非零元素都位于主对角线以及与主对角线平行且紧邻的两条对 角线上,现对该矩阵进行按行压缩存储,若其压储空间用数组 B 表示,A 的元素下标从 0 开 始,B 的元素下标从 1 开始。已知 A[0,0]存储在 B[1],A[n-1,n-1]存储在 B[3n-2],那么非零元素 A[i,j]（0≤i
    A.2i+j-1
    B.2i+j
    C.2i+j+1
    D.3i-j+1

    答案：C
    解析：
    三对角矩阵如下



    将i=0，j=0与1=n-1，j=n-1分别带入选项中，可得选项C。

  • 第10题：

    设某n阶三对角矩阵Anxn的示意图如下图所示。若将该三对角矩阵的非零元素按行存储在一维数组B[k]（1≤k≤3×n-2）中，则k与i、j的对应关系是（ ）。

    A.k=2i+j+2
    B.k=i-j+1
    C.k=3i+j-2
    D.k=2i+j-2

    答案：D
    解析：
    本题考查数据结构基础知识。解答该问题需先计算排列在Ai，j之前的元素个数。在按行存储方式下，存储在Ai，j之前的元素分为i-1行，除第1行外，每行3个元素。在第i行上，Ai，j之前的元素个数分为三种情况：i＞j时为0个，i=j时有1个，i＜j时为2个，概括为j-i+1个。综上，排列在Ai，j之前的元素个数为(i-1) ×3-1+j-i+1，即2i+j-3。由于数组B的下标从1开始，所以k=2i+j-3+1。

  • 第11题：

    无向图的邻接矩阵是一个（）。

    • A、对称矩阵
    • B、零矩阵
    • C、上三角矩阵
    • D、对角矩阵

    正确答案:A

  • 第12题：

    单选题
    设有一个M*N的矩阵已经存放在一个M行N列的数组x中，且有以下程序段：sum=0;for(i=0;i
    A

    矩阵两条对角线元素之和

    B

    矩阵所有不靠边元素之和

    C

    矩阵所有元素之和

    D

    矩阵所有靠边元素之和


    正确答案： A
    解析：
    程序执行过程为：第一个for循环实现对第一列和第N列求和。第二个for循环在上一个for循环结果上实现对第一行和第M行从第二个元素到第N-1个元素的求和，总体来说，就是矩阵所有靠边元素之和，答案选择D选项。

  • 第13题：

    节点导纳矩阵的特点有()。

    A、是n×n阶方阵

    B、是稀疏矩阵

    C、一般是对称矩阵

    D、其对角元一般小于非对角元


    正确答案：ABC

  • 第14题：

    将一个n阶三对角矩阵A的三条对角线上的元素按行压缩存放于一个一维数组B中， A[0][0]存放于B[0]中。对于任意给定数组元素A[i][j]，它应是数组A中第______行的元素。


    正确答案：2i+j-3
    2i+j-3 解析：在三对角矩阵中，按行压缩存储，其转换公式为k=2i+j-3。

  • 第15题：

    下列程序的功能是( )。 main() { static int s[3][3]={1，2，3，4，5，6，7，8，9，)，m，n； for(m=0；m＜3；m++) { for(n=0；n＜=m；n++) printf("%d"，s[m][n])；printf("\n')； } }

    A．输出3×3矩阵的下三角的元素

    B．输出3×3矩阵的上三角的元素

    C．输出3×3矩阵的对角线上的元素

    D．输出3×3矩阵的元素


    正确答案：A
    解析：本题使用了一个双重for循环，外循环变量m的变化范围是0～2，而内循环变量n的变化范围从0～m，所以执行循环体时(m，n)的值依次为(0，0)，(1，0)，(1，1)，(2，0)，(2，1)，(2，2)，故输出的是3×3矩阵的下三角元素。所以应该选择A。

  • 第16题：

    设n阶矩阵A与对角矩阵相似,则().

    A.A的n个特征值都是单值
    B.A是可逆矩阵
    C.A存在n个线性无关的特征向量
    D.A一定为n阶实对称矩阵

    答案：C
    解析：
    矩阵A与对角阵相似的充分必要条件是其有n个线性无关的特征向量，A有n个单特征值只是其可对角化的充分而非必要条件，同样A是实对称阵也是其可对角化的充分而非必要条件，A可逆既非其可对角化的充分条件，也非其可对角化的必要条件，选(C).

  • 第17题：

    设A为n阶实对称矩阵,下列结论不正确的是().

    A.矩阵A与单位矩阵E合同
    B.矩阵A的特征值都是实数
    C.存在可逆矩阵P,使P^-1AP为对角阵
    D.存在正交阵Q,使Q^TAQ为对角阵

    答案：A
    解析：
    根据实对称矩阵的性质，显然(B)、(C)、(D)都是正确的，但实对称矩阵不一定是正定矩阵，所以A不一定与单位矩阵合同，选(A).

  • 第18题：

    设n阶矩阵A满足（aE-A）(bE-A)=O且a≠6.证明：A可对角化.


    答案：
    解析：
    【证明】由(aE-A)(bE-A)=O，得|aE-A|·|bE-A|=0，则|aE-A|=0或者
    |bE-A|=0.又由(aE-A)(bE-A)=O，得r(aE-A)+r(bE-A)≤n.
    同时r（aE-A）+r(bE-A)≥r［(aE-A)-(bE-A)］=r［（a-b）E］=n，
    所以r(aE-A)+r(bE-A)=n.
    (1)若|aE-A|≠0，则r（aE-A=n，所以r(bE-A)=0，故A=bE.
    (2)若|bE-A|≠0，则r(bE-A)=n，所以r(aE-A)=0，故A=aE.
    (3)若|aE-A|=0且|bE-A|=0，则a，b都是矩阵A的特征值.
    方程组(aE-A)X=0的基础解系含有n-r（aE-A）个线性无关的解向量，即特征值a对应的线性无关的特征向量个数为n-r（aE-A）个；
    方程组(bE-A)X=0的基础解系含有n-r(bE-A)个线性无关的解向量，即特征值b对应的线性无关的特征向量个数为n-r(bE-A)个.
    因为n-r(aE-A)+n-r(bE-A)=n，所以矩阵A有n个线性无关的特征向量，所以A一定可以对角化.

  • 第19题：

    设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.


    答案：
    解析：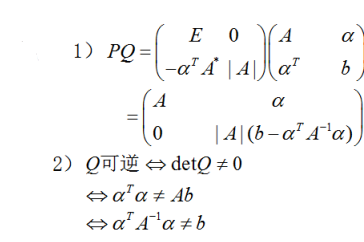

  • 第20题：

    下面的说法中，不正确的是()。

    A.对角矩阵只需存放非零元素即可
    B.稀疏矩阵中值为零的元素较多，因此可以采用三元组表方法存储
    C.稀疏矩阵中大量值为零的元素分布有规律，因此可以采用三元组表方法存储
    D.对称矩阵只需存放包括主对角线元素在内的下(或上)三角的元素即可

    答案：C
    解析：
    稀疏矩阵中大量值为零的元素分布没有规律，因此采用三元组表存储。如果零元素的分布有规律，就没有必要存储非零元素的行号和列号，而需要按其压缩规律找出相应的映象函数。

  • 第21题：

    设某n阶三对角矩阵Anxn的示意图如下图所示。若将该三对角矩阵的非零元素按行存储在一维数组B[k]（1≤k≤3*n-2）中，则k与i、j的对应关系是（ ）。

    A.k=2i+j-2
    B.k=2i-j+2
    C.k=3i+j-1
    D.K=3i-j+2

    答案：A
    解析：
    本题考查数据结构基础知识。解答该问题需先计算排列在Ai,j之前的元素个数。在按行存储方式下，存储在Ai,j之前的元素分为i-1行，除第1行外，每行3个元素。在第i行上，Ai,j之前的元素个数分为三种情况：i＞j时为0个，i=j时有1个，i ＜ j时为2个，概括为j-i+1个。综上，排列在Ai,j之前的元素个数为(i-1)×3-1+j-i+1，即2i+j-3。由于数组B的下标从1开始，所以k=2i+j-3+1。

  • 第22题：

    若一个n阶矩阵A中的元素满足：Aij=Aji（0<=I，j<=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。


    正确答案:上；三角矩阵

  • 第23题：

    问答题
    试证若n阶矩阵A满足A2－A＝2E，则A一定相似于对角矩阵。

    正确答案：
    设λ是矩阵A的特征值,则矩阵f(A)=A2-A-2E的特征多项式为f(λ)=λ2-λ-2,所以有矩阵A的特征值只可能是2或-1。
    ①当λ=-1是A的特征值,而λ=2不是A的特征值,则有,A-2E,≠0,即(A-2E)可逆。由A2-A-2E=0得(A-2E)(A+E)=0,所以有(A-2E)-1(A-2E)(A+E)=(A-2E)-1·0,即A+E=0,A=-E。因此A相似与对角矩阵-E。
    ②当λ=2是A的特征值,而λ=-1不是A的特征值,同理于①,可得矩阵A相似与对角矩阵2E。
    ③当λ=2和λ=-1都是A的特征值,由(A-2E)(A+E)=0知r(A-2E)+r(A+E)≤n。又r(A-2E)+r(A+E)=r(2E-A)+r(A+E)≥r(2E-A+A+E)=r(3E)=n,所以r(A-2E)+r(A+E)=n,即[n-r(A-2E)]+[n-r(A+E)]=n。故两方程组(A-2E)X(→)=0(→)和(A+E)X(→)=0(→)的基础解系所含解向量的个数之和为n,所以A有n个线性无关的特征向量,故其可相似于对角矩阵。
    解析： 暂无解析

  • 第24题：

    填空题
    若一个n阶矩阵A中的元素满足：Aij=Aji（0<=I，j<=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。

    正确答案： 上,三角矩阵
    解析： 暂无解析

相关内容