9、两个随机变量相互独立时，可以由边缘分布得到联合分布

第1题：

设两个相互独立的随机变量X和Y分别服从正态分布N(0，1)和N(1，1)，则

答案：B

解析：

【简解】首先应看到，X+Y和X-Y均为一维正态分布的随机变量.其次要看到，如果z～N(μ，σ^2)，则，反之，如果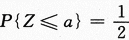，则必有a=μ.因为正态分布的概率密度有对称性.有考生在求解过程中将X+Y和X-Y都进行标准化，更有考生把X+Y和X-Y都看成二维正态随机变量的函数来求解，就更复杂化了.

第2题：

设二维随机变量(X,Y)的联合密度函数为f(x,y)=
　　(1)求随机变量X,Y的边缘密度函数；
　　(2)判断随机变量X,Y是否相互独立；
　　(3)求随机变量Z=X+2Y的分布函数和密度函数.

答案：

解析：

第3题：

设随机变量X与Y相互独立,下表列出二维随机变量(X,Y)的联合分布律及关于X和Y的边缘分布律的部分数值,试将其余的数值填入表中空白处.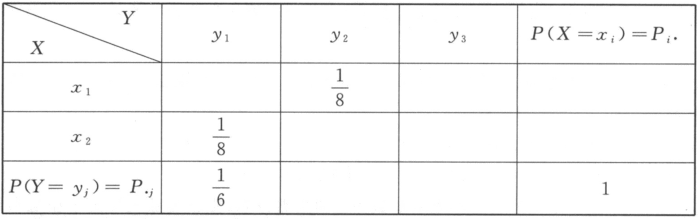

答案：

解析：

第4题：

设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3.
　　设随机变量U=max{X,Y},V=min{X,Y}.
　　(1)求二维随机变量(U,V)的联合分布；(2)求Z=UV的分布；
　　(3)判断U,V是否相互独立？(4)求P（U=V）.

答案：

解析：

第5题：

下列取值分布中，可以作为离散型随机变量的分布列的是（ ）。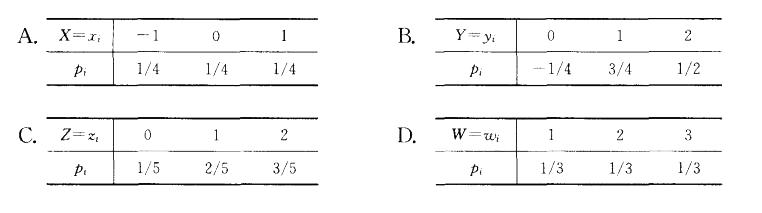

答案：D

解析：

。离散型随机变量的分布列应有以下性质: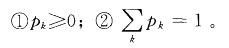

第6题：

下列选项中正确的是（）。

• A、两个泊松分布之差还是泊松分布
• B、若两个二维分布有相同的边缘分布，则它们一定相同
• C、若X为随机变量且X2服从χ2分布，则X服从正态分布
• D、任意两个分布函数之和一定还是分布函数
• E、以上选项都不正确

第7题：

若随机变量X与Y相互独立，且X服从N（1，9），Y服从N（2，6），则X+Y服从（）分布。

第8题：

设随机变量X服从正态分布N（-1，9），则随机变量Y=2-X服从（）．

• A、正态分布N（3，9）
• B、均匀分布
• C、正态分布N（1，9）
• D、指数分布

第9题：

第10题：

第11题：

第12题：

第13题：

设随机变量X,Y相互独立,它们的分布函数为Fx(x),F(y),则Z=min{X,Y}的分布函数为().

第14题：

设二维随机变量(X,Y)的联合分布律为
　　
　　则在Y=1的条件下求随机变量X的条件概率分布.

答案：

解析：

【解】因为P（Y=1）=0.6，
所以

第15题：

随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为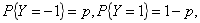令Z=XY。X与Z是否相互独立

答案：

解析：

因为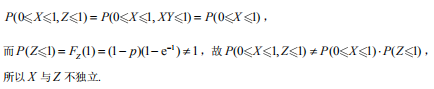

第16题：

设随机变量X和Y相互独立，下表列出了二维随机变量(X，Y)的联合分布律及关于X和关于Y的边缘分布律中的部分数值.试将其余数值填入表中的空白处.
　　

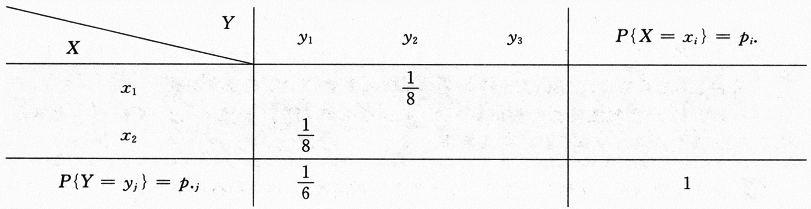答案：

解析：

当离散型随机变量(X，Y)中X与Y相互独立时，有进一步就有，也就是说(X，Y)的分布律中，当X，Y独立就对应各行成比例.有了这一点再加上边缘分布性质，就能很快解得

第17题：

如果两个随机变量A和B均服从正态分布，即A＝N（500，0.05），B＝N（200，0.02），则随机变量A在0.05之间分布的百分数与随机变量B在0.02之间分布的百分数（）。

第18题：

下列叙述中错误的是（）.

• A、联合分布决定边缘分布
• B、边缘分布不能决定决定联合分布
• C、两个随机变量各自的联合分布不同，但边缘分布可能相同
• D、边缘分布之积即为联合分布

第19题：

UE在小区接收信号电平是两个随机变量之和，一个是（）随机变量，符合（）分布；另一个是（）随机变量，符合（）分布。

第20题：

如果随机变量X和Y服从联合正态分布，且X与Y的协方差为0，则X与Y相互独立。

第21题：

第22题：

第23题：

第24题：