已知生产函数Q=-L3+24L2+240L,求:在生产的三个阶段上,L的投入量分别应为多少?
题目
已知生产函数Q=-L3+24L2+240L,求:在生产的三个阶段上,L的投入量分别应为多少?
相似考题
更多“已知生产函数Q=-L3+24L2+240L,求:在生产的三个阶段上,L的投入量分别应为多少? ”相关问题
-
第1题:
已知生产函数为: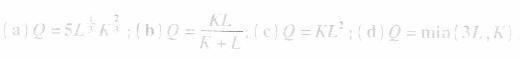
求:(1)厂商长期生产的扩展线方程。 (2)当PL =1、PK=1、Q=1000时,厂商实现最小成本的要素投入组合。答案:解析:

-
第2题:
假设某公司短期的生产函数为Q=72L+15L2-L3,其中Q、L分别代表一定时间内的产量和可变要素的投入量,求(1)导出AP1和MP1的函数;(2)当L=7时,MP1时多少?(3)当L由7个单位增加到8个单位的时候,产量增加多少?(4)L的投入量多大时,MP1将面临递减?(5)该公司的最大的产量时多少?为了达到这个最大的产量,L的投入量时多少?
(1)根据AP=Q/L和已知的生产函数可以得出,AP=72+15L-L 2 。 根据MP=dQ/dL和已知的生产函数可以得出, MP=72+30L-3L 2 。 (2)将L=7代人边际产量函数,可得出MP=135。 (3)将L=7和L=8分别代人生产函数求出两个总产量,二者的差额即为产量增量,为128。 (4)M'=0时,其面临递减,则可以求出L=5。 (5)MP=0时,TP最大,因此可以得出L=12。再代入TP函数,即可以得出最大的产量为1296 -
第3题:
【计算题】已知某企业的生产函数 Q= (-2/3)L³+10L²,确定L的合理投入区域。
规模报酬递增阶段 -
第4题:
某企业生产一种产品,劳动为唯一可变要素,固定成本既定。短期生产函数Q=-0.1L3+6L22+12L,求: (1)劳动的平均产量函数和边际产量函数。 (2)企业雇用工人的合理范围是多少? (3)若已知劳动的价格为W=480,产品Q的价格为40,则当利润最大时,企业生产多少产品Q?
(1)平均产量AP=TP/L= -0.1 L2 +6L+12 边际产量MP=(TP)’= - 0.3 L2+12L+12
(2)企业应在平均产量递减,边际产量为正的生产阶段组织生产,因此雇用工人的数量也应在此范围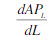 <0,MP>0内。 对APL求导,得
<0,MP>0内。 对APL求导,得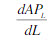 = - 0.2 L +6=0。 即L=30
= - 0.2 L +6=0。 即L=30
当L=30时,APL取得最大值,L>30,APL开始递减。 令MPL= - 0.3L2+12L+12=0,得L=40.98
所以,企业雇用工人的合理范围为30≤L≤41
(3)利润π=PQ-WL=40(- 0.1 L3 +6L2 +12L)-480L = - 4 L3 +240L2 +480L-480L
Π’=- 12L2+480L,当Π’=0时, L=0 (舍去) 或L=40.
当L=40时, Π” <0,所以L=40,利润π最大。
此时,产量Q= -0.1×403+6 × 402 +12 × 40 =3680
略 -
第5题:
已知生产函数Q=f(L,K)=2KL- 0.5L2-0.5K2,假定厂商目前处于短期生产,且K=10,求: (1)写出在短期生产中该厂商关于劳动的总产量TPL函数、劳动的平均产量APL函数和劳动的边际产量MPL函数。 (2)分别计算当总产量TPL、劳动平均产量APL和劳动边际产量MPL各自达到极大值时的厂商劳动的投入量。 (3)什么时候APL=MPL?它的值又是多少?
(1)短期生产中K是不变的,短期关于劳动的总产量函数为:

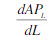 <0,MP>0内。 对APL求导,得
<0,MP>0内。 对APL求导,得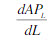 = - 0.2 L +6=0。 即L=30
= - 0.2 L +6=0。 即L=30