圆锥的底面半径为4，母线长为5，那么它的侧面积是__________。

题目
圆锥的底面半径为4，母线长为5，那么它的侧面积是__________。

相似考题

1.求下面各圆柱的侧面积。 （1）底面周长是1.6m，高0.7m。 （2）底面半径是3.2dm，高5dm。

2.圆锥的底面半径为8，母线长为9，则该圆锥的侧面积为（ ）．（A）36л （B）48л （C）72л （D）144л

3.避雷线的保护范围是以避雷线高度h为高,底面半径也为h的一个圆锥体。()此题为判断题(对，错)。

4.一个圆柱的侧面积是188.4dm²，底面半径是2dm。它的高是多少？

参考答案和解析
答案：
解析：
更多“圆锥的底面半径为4，母线长为5，那么它的侧面积是__________。”相关问题

  • 第1题：

    避雷针的保护范围为以避雷针高度h为高,1.5h为底面半径的一个圆锥体。()

    此题为判断题(对，错)。


    参考答案：错误

  • 第2题：

    若一个圆锥的底面圆的周长是4πcm，母线长是6cm，则该圆锥的侧面展开图的圆心角的度数是

    (A)40° (B)80° (C)120° (D)150°


    正确答案：C

  • 第3题：

    ：已知圆柱的母线长是10cm，侧面积是40~cm2，则这个圆柱的底面半径是（ ）。

    A．1.5cm

    B．2.5cm

    C．2cm

    D．3cm


    正确答案：C
    设圆柱的底面半径是r，根据题意可知：40=2r×10，所以r=2cm。正确答案为C。

  • 第4题：

    圆锥体的底面积为2m2,高度为3m,它的体积为()。

    A、1m3

    B、2m3

    C、3m3

    D、4m3


    参考答案：B

  • 第5题：

    一个圆锥的侧面展开图是半径为8 cm，圆心角120°的扇形，则此圆锥底面半径是( )。



    答案：B
    解析：
    由圆锥侧面展开图的半径和圆心角可得出扇形的弧长，扇形的弧长则为底面圆的周长，

  • 第6题：

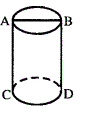    正圆柱体的高为10cm，底面半径为那么，在圆柱体的表面，从A点到D点的最短距离为（ ）。


    答案：B
    解析：
    沿AC这条线把圓柱剪开，由题意可得，其展开图的矩形的宽为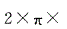，长为10cm，D为其一边长的中点，故从A点到D点的最短距离为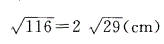故选 B。

  • 第7题：

    已知正圆锥的底面半径是1cm，母线为3cm，P为底面圆周上一点，由P绕过圆锥回到P点的最短路径如图所示，由顶点V到这条路线的最小距离是多少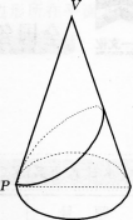


    答案：
    解析：
    圆锥的曲面沿着母线剪开，展开成一个平面(如下图)，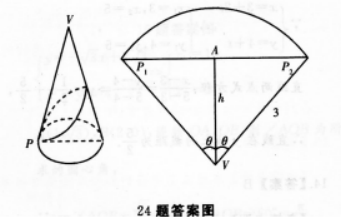

    其半径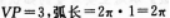的扇形
    短距离，就是弦PlP2，由V到这条路线的最短距离是图中的线段h=AV．依据弧长公式2π=2θ·3，得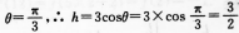

  • 第8题：

    桌面上有一倒立的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴(图中虚线)与桌面垂直，过轴线的截面为等边三角形，如图5所示，有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上，光束的中心轴与圆锥的轴重合。已知玻璃的折射率为1．5，则光束在桌面上形成的光斑半径为()。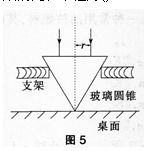

    A.R

    B.1．5r

    C.2r

    D.2．5r

    答案：C
    解析：
    玻璃的折射率为1．5，可得临界角小于450。经过第一次折射时．由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折。当第二次折射时，由于入射角等于60。。所以光会发生全反射，反射光线恰好垂直射出。因为0N等于r，则0A等于2r，由于LMOA=LAM0=30。，所以AM等于2r。故本题选C。

  • 第9题：

    正圆锥底面直径为D，高为H，边长为L，其表面积A=（）。


    正确答案:A=（π*D*D/4）+（π*D*L/2）

  • 第10题：

    若圆柱的底面半径为5cm，高为4cm，则圆柱的侧面积为（）平方厘米。


    正确答案:40π

  • 第11题：

    单选题
    若圆柱的底面圆半径为5cm，髙为4cm，则圆柱的侧面积为（）
    A

    20πcm2

    B

    40πcm2

    C

    80πcm2

    D

    90πcm2


    正确答案： A
    解析： 暂无解析

  • 第12题：

    填空题
    若圆柱的底面半径为5cm，高为4cm，则圆柱的侧面积为（）平方厘米。

    正确答案： 40π
    解析： 暂无解析

  • 第13题：

    下列关于圆锥及投影作图方法说法有误的一项是()

    A.圆锥底面为水平圆时，其正面投影和侧面投影积聚为正平线

    B.绘制圆锥投影时，通常最后画出圆锥在各投影位置上的对称中心线

    C.圆锥的轴线垂直于水平面时，圆锥底面为水平圆

    D.圆锥是由底面和圆锥面组成的


    参考答案：A

  • 第14题：

    一个长方形铁锭，底面周长为32厘米，长与宽的比是3︰1，高比宽短30%。用它刚好可以铸成高为6厘米的圆锥体，那么圆锥体的底面积为（ ）平方厘米。

    A．67.2

    B．201.6

    C．537.6

    D．1612.8


    正确答案：A
    先求出长方体的长、宽、高。

  • 第15题：

    一圆锥的侧面积恰好等于其底面积的2倍，则该圆锥侧面展开图所对应扇形圆心角的度数为_________。


    正确答案：
    180° [解析]设圆锥底面半径为r，母线长为l，则πrl=2πr2，即l=2r，故扇形圆心角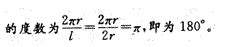

  • 第16题：

    今有底面半径和高均为1的圆柱体与底面半径和高均为2的圆柱体，共计15个，表面积和为120π。那么底面半径和高均为2的圆柱体有多少个?

    A．4

    B．5

    C．6

    D．7


    正确答案：B
    [答案] B。[解析]底面半径和高均为1的圆柱体的表面积为2×π×12+2×π×1×1=4π，半径和高均为2的圆柱体的表面积为2×π×22×π×2×2=16π。则半径和高均为2的圆柱体有(120π-15×4π)+(16π-4π)=5个。

  • 第17题：

    一实心圆锥体的底面半径为r，母线长为2r。若截圆锥体得到两个同样的椎体（如下图所示），则所得两个椎体的表面积之和与原圆椎体表面积的比值是（ ）


    A． B． C． D．

    答案：C
    解析：
    由圆锥体的底面半径为r，母线长为2r，可得圆锥体的表面积为。
    所截得的两个锥体的表面积之和要比原圆锥体的表面积多两个等边三角形截面的面积，等边三角形的边长为2r，则其面积为，所以两个锥体的表面积之和为。则两个锥体的表面积之和与原锥体表面积比值是。C项当选。

  • 第18题：

    如图，圆锥高厘米，底面半径为6厘米，一只蚂蚁从A.点沿圆锥侧面爬行到B.点，则最短的距离为_________厘米。



    A.12
    B.
    C.6π
    D.24

    答案：B
    解析：

  • 第19题：

    一个圆柱的侧面展开图是正方形,那么它的侧面积是下底面积的（ ）倍

    A.2
    B.4
    C.4π
    D.π
    E.2π

    答案：C
    解析：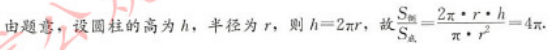

  • 第20题：

    计算题：有一个圆锥形的防雨罩，它的底面圆直径是20cm，母线长是15cm，求做这个防雨罩所用的扇形铁皮的圆心角和面积？


    正确答案: 扇形的半径R＝圆锥的母线长b＝15cm，圆锥的底面半径r＝20/2＝10cm，
    设扇形的弧长为L，圆心角度数为n，面积为S。
    ∵L＝2πr＝（n•π•B./180
    即：nπ×15/180＝2π×10
    ∴n＝2×10/15×180＝240°
    ∴S＝πrL＝3.14×10×15
    ＝471（cm2）
    防雨罩扇形圆心角为240°，面积为471cm2。

  • 第21题：

    若圆柱的底面圆半径为5cm，髙为4cm，则圆柱的侧面积为（）

    • A、20πcm2
    • B、40πcm2
    • C、80πcm2
    • D、90πcm2

    正确答案:B

  • 第22题：

    计算题：正圆锥侧表面展开后已知圆锥底圆直径为D，素线长度为L求出扇形圆心角α的公式。


    正确答案: α/360°＝π×D/（2×π×L）
    α＝180°×D/L
    答：扇形圆心角α＝180°D/L

  • 第23题：

    填空题
    已知正六棱柱的高是5cm，底面外接圆半径是4cm，则这正六棱柱的侧面积是____．

    正确答案： 120cm2
    解析：
    正六棱柱的底面为一正六边形，根据正六边形的性质可得其周长为C＝6r＝24cm，则该六棱柱的侧面积为S＝Ch＝24×5＝120cm2．

相关内容