下面是某同学解方程的过程：求方程x(x-l)=x。解：x(x-1)=x，两边同时除以x得x=2。问题： (1)该同学的解题过程哪一步错了分析原因； (2)针对该生的情况，请你设计一个教学片段，并说明教学意图； (3)怎样防范这样的错误

题目
下面是某同学解方程的过程：求方程x(x-l)=x。解：x(x-1)=x，两边同时除以x得x=2。问题：
(1)该同学的解题过程哪一步错了分析原因；
(2)针对该生的情况，请你设计一个教学片段，并说明教学意图；
(3)怎样防范这样的错误

相似考题

1.曲线y=x^3＋x－2在点(1,0)处的切线方程是()A、y=2(x-1)B、y=4(x-1)C、y=4x-1D、y=3(x-1)

2. 小颖碰到这样一道解方程的题：2x=5x，她在方程的两边都除以x，竟然得到 2=5.你能说出她错在哪里吗？

3.能正确表示代数式的C语言表达式是( )A．3*xn／(2*x-1)B．3*x**n／(2*x-1)C．3*pow(x，n)*(1／(2*x-1))D．3*pow(n，x)／(2*x-1)

4.解方程。X-0.25=1/4 X/4=30% 4+0.7X=102 2/3X+1/2X=42

更多“下面是某同学解方程的过程：求方程x(x-l)=x。解：x(x-1)=x，两边同时除以x得x=2。问题： ”相关问题

  • 第1题：

    你能求三个不等式5X-1>3(X-1), X/2-1>3-3X/2,X-1<3X+1的解集的公共部分吗？

  • 第2题：

    求下列各式中x的值：

    （1）x3=0.008；（2）x3-3=3/8；（3）（x-1）3=64.

  • 第3题：

    下面是小明同学解不等式(x－5)／2－1<(3x＋2)／2的过程:

    下面是小明同学解不等式(x-5)/2-1<(3x+2)/2的过程：

         去分母，得x+5-1＜3x+2。

         移项、合并同类项，得-2x＜-2。

         两边都除以-2，得x＜1.

         他的解法有错误吗？如果有错误，请你指出错在哪里。 


    2处错误（1）去分母时公分母2漏乘“-1”项

           （2）两边都除以-2时不等号方向没有改变

    正确解法：去分母   x+5-2<3x+2

       移项，合并同类项  -2x<-1

                           x>1/2


  • 第4题：

    用函数的图象求下列方程的解：

    （1）x²-3x+2=0 ;（2）-x²-6x-9=0 ;（3）x²+x+2=0 ; （4）1-x-2x²=0 。

  • 第5题：

    设f（x）=x（x-1）（x-2），则方程



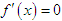
    的实根个数是（　　）。

    A、 3
    B、 2
    C、 1
    D、 0

    答案：B
    解析：
    先对方程求导，得：



    再根据二元函数的判别式



    判断可知方程有两个实根。

  • 第6题：

    已知二次型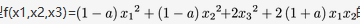的秩为2.(1)求a.(2)求作正交变换X=QY,把f(x1,x2,x3)化为标准形.(3)求方程f(x1,x2,x3)=0的解


    答案：
    解析：

  • 第7题：

    一平面简谐波沿x轴正向传播，已知x=L（L<λ）处质点的振动方程为y=Acosωt，波速为u，则波动方程为（）

    • A、y=Acosω［t-（x-L）／u]
    • B、y=Acosω［t-（x+L）／u]
    • C、y=Acosω［t+（x+L）／u]
    • D、y=Acosω［t+（x-L）／u]

    正确答案:A

  • 第8题：

    在数域F上x^2-3x+2可以分解成（）。

    • A、（x-1）^2
    • B、（x-1）（x-3）
    • C、（x-2）（x-3）
    • D、（x-1）（x-2）

    正确答案:D

  • 第9题：

    填空题
    设y1（x）是方程y′＋P（x）y＝f1（x）的一个解，y2（x）是方程y′＋P（x）y＝f2（x）的一个解，则y＝y1（x）＋y2（x）是方程____的解。

    正确答案： y′+P(x)y=f1(x)+f2(x)
    解析：
    根据题意可知，y1′＋P（x）y1＝f1（x），y2′＋P（x）y2＝f2（x）。两式相加得（y1′＋y2′）＋P（x）（y1＋y2）＝f1（x）＋f2（x）。则可发现y＝y1＋y2是方程y′＋P（x）y＝f1（x）＋f2（x）的解。

  • 第10题：

    单选题
    一平面简谐波沿x轴正向传播，已知x=L（L<λ）处质点的振动方程为y=Acosωt，波速为u，则波动方程为（）
    A

    y=Acosω［t-（x-L）／u]

    B

    y=Acosω［t-（x+L）／u]

    C

    y=Acosω［t+（x+L）／u]

    D

    y=Acosω［t+（x-L）／u]


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    设y1（x）是方程y′＋P（x）y＝f1（x）的一个解，y2（x）是方程y′＋P（x）y＝f2（x）的一个解，则y＝y1（x）＋y2（x）是方程（　　）的解。
    A

    y′＋P（x）y＝f1（x）＋f2（x）

    B

    y＋P（x）y′＝f1（x）－f2（x）

    C

    y＋P（x）y′＝f1（x）＋f2（x）

    D

    y′＋P（x）y＝f1（x）－f2（x）


    正确答案： A
    解析：
    根据题意可知，y1′＋P（x）y1＝f1（x），y2′＋P（x）y2＝f2（x）。两式相加得（y1′＋y2′）＋P（x）（y1＋y2）＝f1（x）＋f2（x）。则可发现y＝y1＋y2是方程y′＋P（x）y＝f1（x）＋f2（x）的解。

  • 第12题：

    单选题
    设f(x)=x(x-1)（x-2），则方程f'(x)=0的实根个数是：
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： A
    解析：

  • 第13题：

    已知（x-1）²=4，求x的值。


    解 （X-1）2=4，得X-1=+2

    即X=1+2，X=3或X=-1


  • 第14题：

    与数学式子应的C语言表达式是

    A．3*xn/(2*x-1)

    B．3*x**n/(2*x-1)

    C．3*pow(x，n)*(1/(2*x-1))

    D．3*pow(n，x)/(2*x-1)


    正确答案：C
    解析：在该题中，x的n次方应该调用函数pow(x，n)计算，pow(x，n)的参数写反了。

  • 第15题：

    求下面函数的返回值（微软）

    int func(x)

    {

    int countx = 0;

    while(x)

    {

    countx ++;

    x = x&(x-1);

    }

    return countx;

    }


    正确答案：

     

    假定x = 9999。答案：8
    思路：将x转化为2进制，看含有的1的个数。

  • 第16题：

    与数学式子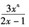对应的C语言表达式是

    A．3*x^n/(2*x-1)

    B．3*x**n/(2*x-1)

    C．3*pow(x，n)*(1/(2*x-1) )

    D．3*pow(n，x)/(2*x-1)


    正确答案：C

  • 第17题：

    不等式|x-1|+|x+2|≥5的解集是________ 。


    答案：
    解析：
    {x,x≤-3或x≥2}。解析：分三种情况讨论，①当x<-2时，原不等式等价于(1-x)+(-x-2)≥5，解得x≤-3；②当-2≤x≤1时，原不等式等价于(1-x)+(x+2)≥5，此时矛盾，不等式无解；③当x>1时，原不等式等价于(x-1)+(x+2)≥5，解得x≥2。综上，该不等式的解集为{x,x≤-3或x≥2}。

  • 第18题：

    将x3+6x-7因式分解为（ ）

    A.（x-1）（x2+x+7）
    B.（x+1）（x2+x+7）
    C.（x-1）（x2+x-7）
    D.（x-1）（x2-x+7）
    E.（x-1）（x2-x-7）

    答案：A
    解析：
    原式=x3-1+6x-6=（x-1）（x2+x+1）+6（x-1）=（x-1）（x2+x+7）.

  • 第19题：

    （x^3-6x^2+11x-6，x^2-3x+2）=（）。

    • A、（x-1）（x+2）
    • B、（x+1）（x-2）
    • C、（x-1）（x-2）
    • D、（x-2）（x-3）

    正确答案:C

  • 第20题：

    单选题
    设f（x）＝x（x－1）（x－2），则方程f′（x）＝0的实根个数是（　　）。[2016年真题]
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： C
    解析：
    先对方程求导，得：f′（x）＝3x2－6x＋2，再根据二元函数的判别式Δ＝b2－4ac＝12＞0，可知方程有两个实根。

  • 第21题：

    单选题
    已知某二阶非齐次线性微分方程的三个解分别为y1＝ex，y2＝xex，y3＝x2ex，则它的通解为（　　）。
    A

    y＝C1（x－1）ex＋C2（x2－1）ex＋ex

    B

    y＝C1（x－1）e－x＋C2（x2－1）ex＋ex

    C

    y＝C1（x－1）ex＋C2（x2－1）e－x＋ex

    D

    y＝C1（x－1）ex＋C2（x2－1）ex＋e－x


    正确答案： A
    解析：
    因为y1＝ex，y2＝xex，y3＝x2ex是二阶非齐次微分方程的特解，故xex－ex，x2ex－ex是该微分方程对应齐次微分方程的两个线性无关的解。故二阶非齐次微分方程的通解为y＝C1（xex－ex）＋C2（x2ex－ex）＋ex，化简可得y＝C1（x－1）ex＋C2（x2－1）ex＋ex。

  • 第22题：

    单选题
    在数域F上x^2-3x+2可以分解成（）。
    A

    （x-1）^2

    B

    （x-1）（x-3）

    C

    （x-2）（x-3）

    D

    （x-1）（x-2）


    正确答案： D
    解析： 暂无解析

  • 第23题：

    单选题
    （x^3-6x^2+11x-6，x^2-3x+2）=（）。
    A

    （x-1）（x+2）

    B

    （x+1）（x-2）

    C

    （x-1）（x-2）

    D

    （x-2）（x-3）


    正确答案： C
    解析： 暂无解析

相关内容