高中数学《偶函数》一、考题回顾二、考题解析 【教学过程】 (一)导出课题 同学们，“对称”是大自然的一种美，这种“对称美”在数学中也有大量的反映.让我们看看下列函数有什么共性? (二)形成概念1.初中函数与高中函数概念的区别? 2.一个函数不是奇函数就是偶函数对吗?如果不对，请举例。

题目
高中数学《偶函数》

一、考题回顾



二、考题解析
【教学过程】
(一)导出课题
同学们，“对称”是大自然的一种美，这种“对称美”在数学中也有大量的反映.让我们看看下列函数有什么共性?
(二)形成概念



1.初中函数与高中函数概念的区别?
2.一个函数不是奇函数就是偶函数对吗?如果不对，请举例。

相似考题

1.若f(x)为奇函数,φ(x)为偶函数,f[φ(x)]且有意义,则f[φ(x)]是()A、偶函数B、奇函数C、非奇非偶函数D、可能是奇函数也可能是偶函数

2.设函数f(x)= xcosx,则该函数是()。A、奇函数B、偶函数C、非奇非偶函数D、既是奇函数又是偶函数

3.A.奇函数 B.偶函数 C.非奇非偶函数 D.周期函数

4.在高中数学中,算法应作为一种核心观念贯穿于高中数学教学的始终。()此题为判断题(对，错)。

更多“高中数学《偶函数》 ”相关问题

  • 第1题：

    函数f（x）=sinx+x3（　　）

    A.是偶函数
    B.是奇函数
    C.既是奇函数，又是偶函数
    D.既不是奇函数，又不是偶函数

    答案：B
    解析：

  • 第2题：

    设函数f（x）是连续且单调增加的奇函数，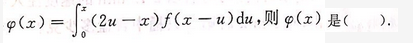

    A.单调增加的奇函数
    B.单调减少的偶函数
    C.单调增加的偶函数
    D.单调减少的偶函数

    答案：B
    解析：

  • 第3题：


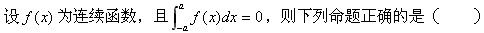    A.f（x）为[-a，a]上的奇函数
    B.f（x）为[-a，a]上的偶函数
    C.f（x）可能为[-a，a]上的非奇非偶函数
    D.f（x）必定为[-a，a]上的非奇非偶函数

    答案：C
    解析：

  • 第4题：

    函数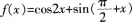是( )。

    A、非奇非偶函数
    B、仅有最小值的奇函数
    C、仅有最大值的偶函数
    D、既有最大值又有最小值的偶函数

    答案：D
    解析：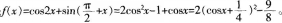

  • 第5题：

    下列关于高中数学课程结构的说法不正确的是（）。

    • A、高中数学课程可分为必修与选修两类
    • B、高中数学选修课程包括4个系列的课程
    • C、高中数学必修课程包括5个模块
    • D、高中课程的组合具有固定性，不能发生改变

    正确答案:D

  • 第6题：

    偶函数加上直流后仍为偶函数。


    正确答案:正确

  • 第7题：

    设f（x）在（-a，a）（a＞0）上连续，F（x）是f（x）的一个原函数，则当f（x）是偶函数时，下面结论正确的是（）。

    • A、F（x）是偶函数
    • B、F（x）是奇函数
    • C、F（x）可能是奇函数，也可能是偶函数
    • D、F（x）是否是偶函数不能确定

    正确答案:D

  • 第8题：

    偶函数加上直流后不是偶函数（）


    正确答案:错误

  • 第9题：

    单选题
    已知f（x）为连续的偶函数，则f（x）的原函数中（）。
    A

    有奇函数

    B

    都是奇函数

    C

    都是偶函数

    D

    没有奇函数，也没有偶函数


    正确答案： D
    解析： 暂无解析

  • 第10题：

    单选题
    A

    非负的实的偶函数

    B

    负的偶函数

    C

    可正可负的偶函数

    D

    可正可负的奇函数


    正确答案： A
    解析：

  • 第11题：

    单选题
    设f（x）是连续的偶函数，则其原函数F（x）一定是（　　）。
    A

    偶函数

    B

    奇函数

    C

    非奇非偶函数

    D

    有一个是奇函数


    正确答案： C
    解析：
    奇函数的导函数是偶函数，但是偶函数的积分不一定是奇函数，因为积分后面要加一个C，C不为0时，为非奇非偶函数；若C＝0，则为奇函数，故F（x）一定有一个是奇函数。

  • 第12题：

    单选题
    函数y=sinx是：（）。
    A

    奇函数

    B

    偶函数

    C

    既是奇函数，又是偶函数

    D

    既不是奇函数又不是偶函数


    正确答案： A
    解析： 暂无解析

  • 第13题：


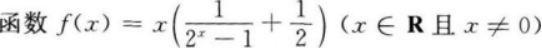    A.是偶函数
    B.既是奇函数又是偶函数
    C.既不是奇函数，也不是偶函数
    D.是奇函数

    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为函数的奇偶性． 【应试指导】


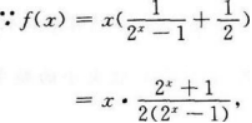
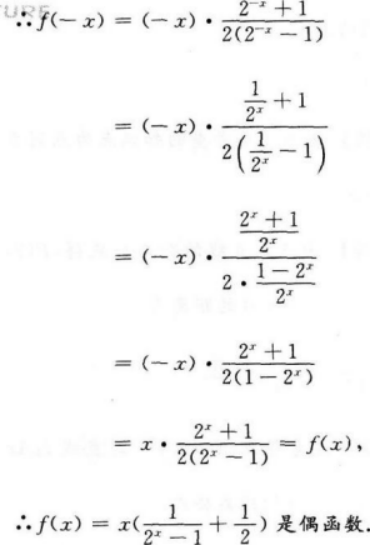
  • 第14题：

    高中数学《曲线与方程》


    答案：
    解析：

  • 第15题：

    下列关于高中数学基础性的说法不正确的是（ ）

    A.高中数学课程为学生进一步学习提高了必要的数学准备
    B.高中数学为不同学生提供相同的基础
    C.高中数学课程体现时代性、基础性和选择性
    D.高中数学课程要以学生的发展为本，尊重他们的个性发展

    答案：B
    解析：
    本题考查高中数学课程的性质

    选项A、C、D都体现了高中数学课程的定位，高中数学课程面向全体学生，为不同兴趣和志向、不同发展方向、进入不同高校不同专业学习的学生提供适合他们的数学基础，高中数学课程为不同学生提供不同的基础。

  • 第16题：

    下列关于高中数学基础性的说法不正确的是（）。

    • A、高中数学课程为学生进一步学习提供了必要的数学准备
    • B、高中数学课程为不同学生提供相同的基础
    • C、高中数学课程体现时代性、基础性和选择性
    • D、高中数学课程要以学生的发展为本，尊重他们的个性发展

    正确答案:B

  • 第17题：

    奇函数与偶函数的乘积函数是（）。

    • A、奇函数
    • B、偶函数
    • C、常数函数
    • D、非奇非偶函数

    正确答案:A

  • 第18题：

    互相关系数是（）

    • A、奇函数
    • B、偶函数
    • C、非奇非偶函数
    • D、零值函数

    正确答案:C

  • 第19题：

    已知f（x）为连续的偶函数，则f（x）的原函数中（）。

    • A、有奇函数
    • B、都是奇函数
    • C、都是偶函数
    • D、没有奇函数，也没有偶函数

    正确答案:A

  • 第20题：

    如果f（t）是t的偶函数，则频谱函数F（jω）是ω的实偶函数。


    正确答案:正确

  • 第21题：

    单选题
    奇函数与偶函数的乘积函数是（）。
    A

    奇函数

    B

    偶函数

    C

    常数函数

    D

    非奇非偶函数


    正确答案： B
    解析： 暂无解析

  • 第22题：

    单选题
    （2013）已知f（x）为连续的偶函数，则f（x）的原函数中：（）
    A

    有奇函数

    B

    都是奇函数

    C

    都是偶函数

    D

    没有奇函数也没有偶函数


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    下列关于高中数学课程结构的说法不正确的是（）。
    A

    高中数学课程可分为必修与选修两类

    B

    高中数学选修课程包括4个系列的课程

    C

    高中数学必修课程包括5个模块

    D

    高中课程的组合具有固定性，不能发生改变


    正确答案： C
    解析： 高中数学课程可分为必修与选修两类，必修课程由五个模块组成，选修课程包括四个系列。高中课程的组合具有一定的灵活性，不同的组合可以相互转换。学生在做出选择之后，可以根据自己的意愿和条件向学校提出申请调整，经过测试获得相应的学分即可转换。

相关内容