如图所示,在边长为24的正方形ABCD上,减去阴影部分四个全等的等腰直角三角形,再沿虚线折起,恰好折成一个立方体包装盒。 这个包装盒容积最大为:
题目
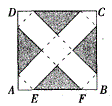
如图所示,在边长为24的正方形ABCD上,减去阴影部分四个全等的等腰直角三角形,再沿虚线折起,恰好折成一个立方体包装盒。 这个包装盒容积最大为:



相似考题
更多“如图所示,在边长为24的正方形ABCD上,减去阴影部分四个全等的等腰直角三角形,再沿虚线折起,恰好折成一个立方体包装盒。 这个包装盒容积最大为: ”相关问题
-
第1题:
矩形截而挖去一个边长为a的正方形,如图所示,该截面对Z轴的惯性矩IZ为 答案:C解析:解:选C
答案:C解析:解:选C 求得。
求得。
知识拓展:

-
第2题:
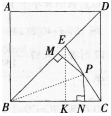
如图,边长为a的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=________。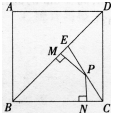 答案:解析:
答案:解析: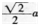
解析:作EK⊥BC于K,连接BP,由△EBC的面积等于△PBE和△PBC的面积之和且BE=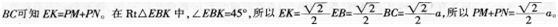
-
第3题:
如图所示,一个边长为16厘米的大正方形,在距离角一定位置处与对角线平行折叠四次,得到中部小正方形的边长为4厘米。如果CB与大正方形的对边平行,则三角形ABC的面积为( )。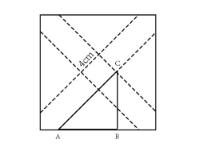 A.32
A.32
B.16
C.16
D.24答案:A解析:第一步,本题考查几何问题,属于平面几何类。
第二步,如下图所示,由于正方形的对角线互相垂直且平分,过正方形的中心做平行于底边的一条线,容易看出这条线过C点(否则小正方形对角线将不能垂直平分)。可知BC长度为正方形边长的一半,即16÷2=8厘米。由中心是小正方形,则∠ABC是直角的一半即45°,可知△ABC是一个等腰直角三角形,面积为8×8÷2=32(平方厘米)。
-
第4题:
某小区规划建设一条边长为10米的正方形绿地。如图所示,以绿地的2个顶点为圆心,边长为半径分别作扇形,把绿地划分为不同的区域。小区现准备在图中阴影部分种植杜鹃,则杜鹃种植面积为( )平方米。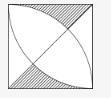 A.100-25π
A.100-25π
B.200-35π
C.200-50π
D.100π-100答案:A解析:第一步,本题考查几何问题,用割补平移法解题。
第二步,阴影部分为不规则图形,考虑割补平移解题,将左下方阴影部分平移到右上方的空白部分,则阴影面积为右上部分面积,即正方形面积-四分之一圆的面积。
第三步,正方形的面积为10×10=100(平方米),四分之一圆的面积为π×102÷4=25π(平方米),那么阴影部分的面积为(100-25π)平方米。
因此,选择A选项。 -
第5题:
如右图所示,幼儿园老师用边长为10cm的正八边形纸皮,裁去四个同样大小的等腰直角三角形,做成长方体包装盒。如果用该包装盒存放体积为的立方体积木(不凸出包装盒外沿),那么,这个盒子最多可以放入多少块积木
 A.75
A.75
B.80
C.85
D.90答案:A解析:
-
第6题:
如图,由四个全等的直角三角形拼成一个大正方形,每个三角形的面积都是1,且两直角边之比大于等于2,则这个大正方形的面积至少是()。 A.4
A.4
B.5
C.6
D.7答案:B解析:第一步,本题考查几何问题,属于平面几何类。
第二步,根据图形可知大正方形面积=4个三角形面积+小正方形面积=4+小正方形面积,小正方形边长=三角形长直角边-短直角边,那么当三角形两直角边差最小时,可得大正方形面积最小,由于两直角边之比大于等于2,即当两直角边之比等于2时,大正方形面积最小。
第三步,设三角形短直角边为a,则长直角边为2a,三角形的面积为
解得a=1,所以小正方形的面积为(2a-a)2=1×1=1,故大正方形面积至少为4+1=5。
因此,选择B选项。 -
第7题:
用边长为120cm的正方形铁皮做一个无盖水箱,先在四角分别截去一个边长相等的小正方形,然后把四边垂直折起焊接而成,问剪去的小正方形的边长为多少时,水箱容积最大最大容积是多少答案:解析:设剪去的小正方形边长为x(cm),则水箱底边长为120-2x,则水箱容积为
∴剪去的小正方形边长为20cm时水箱容积最大为128000cm3. -
第8题:
图6-18是一个边长为10的正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,则阴影部分的面积为( )
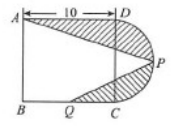
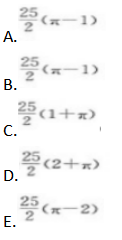 答案:C解析:
答案:C解析:
-
第9题:
以下为一个立方体的外表面,下列哪个立方体可以由此折成?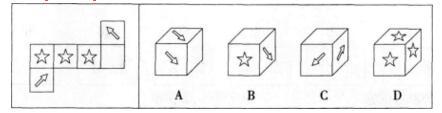 A.如图
A.如图
B.如上图
C.如上图示
D.如图所示答案:B解析:含箭头的两个面是相对面不可能相邻,排除A、C;含五角星的三面不可能两两相邻,排除D;B项可由左边展开图折成。 -
第10题:
使用圆形包装盒包装的高档帽子.不需要再捆扎。
正确答案:错误 -
第11题:
蒙牛牛奶的纸包装盒(容积为250ml,在铝箔、纸板外涂有聚乙烯,主要材料为纸,已印有图案,可折叠)
正确答案:48191000 -
第12题:
单选题哪些药物不能内服?()A药品包装盒上印有正方形红底白字“外”字标示的外用药。
B药品包装盒上印有正方形白底红字“外”字标示的外用药。
C药品包装盒上印有正方形红底白字“内”字标示的外用药。
D药品包装盒上印有正方形白底红字“内”字标示的外用药。
正确答案: D解析: 暂无解析 -
第13题:
如右图所示,幼儿园老师用边长为250px的正八边形纸皮,裁去四个同样大小的等腰直角三角形,做成长方体包装盒。如果用该包装盒存放体积为200px3的立方体积木(不凸出包装盒外沿),那么,这个盒子最多可以放入多少块积木?
 A. 75
A. 75
B. 80
C. 85
D. 90答案:A解析:知识点:面积计算
立方体的体积200px3,则边长为50px,而盒子的的底面为250px×250px,则每一层最多可以放25个。盒子的高为等腰直角三角形的直角边长,2a2=100,得到a= ≈175px,则最多可以放3层。故最多可以放25×3=75个。因此,答案选择A。 -
第14题:
劳动技能课上老师给出一道手工题:一张正方形纸片,在一对对角处各减去一个边长为1厘米的小正方形(如右图所示),想办法把这个缺角的正方形恰好剪成一些长2厘米、宽1厘米的小矩形,问初始的大正方形边长要多大时,任务才有可能完成
 A.8厘米
A.8厘米
B.15厘米
C.32厘米
D.以上答案都不对答案:D解析:第一步,本题考查几何问题中的几何构造。第二步,首先排除B选项15,15×15=225,去除两个角为223,不能被2整除,所以排除;再验证剩余偶数选项,以4×4为例,标数如下图,发现被拿掉的为1和13,不管n×n,拿去的两个位置奇偶性一定相同,所以拿去的数字之和为偶数,再看剩余,要2×1的长方形,一定是挨着的两个正方形组成,挨着的两个正方形奇偶性不同,加和为奇数,验证8×8,总共64个格,去除两个角还剩62个,可组成31个2×1的长方形,每个和都是奇数,所以奇数×31还是奇数,加上两个角的偶数应该为奇数,但是1+2+3+……+63+64为偶数,不满足,同理32×32也不满足。
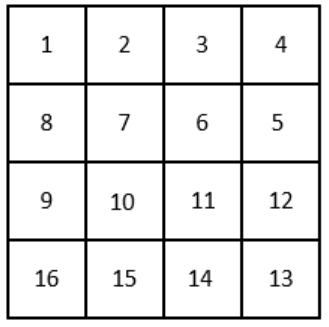
第三步,A、B、C选项都不满足,因此以上答案都不对。因此,选择D选项。 -
第15题:
将右边的箔片沿虚线折起来,便可做一个正方体。问这个正方体的3号面对面是几号面?( )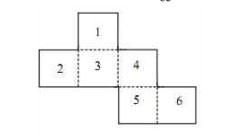 A. 1
A. 1
B. 2
C. 5
D. 6答案:D解析:从图可以容易看出1.2.4都与3相邻,当沿着虚线折起来时,5号也与3号相邻。故答案为D。 -
第16题:
下列四块纸板均由六个正方形组成,问沿虚线折叠,能折成正方体的有几个? A.1
A.1
B.2
C.3
D.4答案:D解析:四个图形都可折成立方体,选D。立方体共有以下11种展开方式:
-
第17题:
在边长为1的正方形ABCD中,AC与BD相交于O,以A、B、C、D分别为圆心,以对角线长的一半为半径画圆弧与正方形的边相交,如图,则图中阴影部分的面积为多少?(π=3.14)
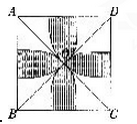 A.0.43
A.0.43
B.0.57
C.0.64
D.0.71答案:C解析:
-
第18题:
劳动技能课上老师给出一道手工题:一张正方形纸片,在一对对角处各减去一个边长为1厘米的小正方形(如右图所示),想办法把这个缺角的正方形恰好剪成一些长2厘米、宽1厘米的小矩形,问初始的大正方形边长要多大时,任务才有可能完成? A.8
A.8
B.15
C.32
D.以上答案都不对答案:D解析:将大正方形拆分为若干个边长 1 厘米的小正方形,根据大正方形边长的奇偶性分类讨论如下:
①若大正方形的边长为奇数,则小正方形的个数也为奇数,剪去 2 个小正方形后,剩下的小正方形个数依
然为奇数;而每个小矩形需要占用 2 个小正方形,则剩下的奇数个小正方形不可能全部拆成小矩形,矛盾。故 边长为奇数必然不满足题意,排除 B 项;
②若大正方形的边长为偶数,如下图所示:将其拆分为若干个小正方形之后,黑色和白色方块的总数相等, 且拿掉的对角的两个小正方形一定都是黑色或白色,那么剩下的黑色与白色方块数必然不等,此为结论 1。
观察图形,要取出 2×1 的小矩形,必须由一黑一白组成。那么,要让剩下的图形恰好能分成若干个 2×1 的小矩形,则剩下图形的黑色与白色方块个数必须相等,此为结论 2。
结论 2 与结论 1 明显矛盾,故边长为偶数也必须不满足题意,排除 A、C 项。 故正确答案为 D。
-
第19题:
如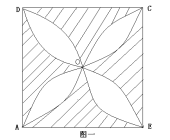 ,四边形ABCD是边长为1的正方形,弧AOB,BOC,COD,DOA均为半圆,则阴影部分的面积为
,四边形ABCD是边长为1的正方形,弧AOB,BOC,COD,DOA均为半圆,则阴影部分的面积为
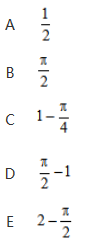 答案:E解析:
答案:E解析: -
第20题:
矩形截面挖去一个边长为a的正方形,如图所示,该截面对z轴的惯性 答案:C解析:
答案:C解析:
-
第21题:
如图9所示的“勾股树”中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为12cm,则A、B、C、D四个小正方形的面积之和为__________。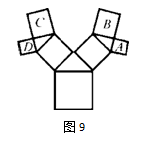 答案:解析:144
答案:解析:144 -
第22题:
哪些药物不能内服?()
- A、药品包装盒上印有正方形红底白字“外”字标示的外用药。
- B、药品包装盒上印有正方形白底红字“外”字标示的外用药。
- C、药品包装盒上印有正方形红底白字“内”字标示的外用药。
- D、药品包装盒上印有正方形白底红字“内”字标示的外用药。
正确答案:A -
第23题:
ABCD是边长为L的正方形的四个顶点,若在A、B、C、D四个顶点处分别放置带电量为q的正点电荷,则A、B、C、D四点电荷在正方形对角线交点上产生的合场强的大小为()。
正确答案:0
