在下图中，大圆的半径是8。求阴影部分的面积是多少? A. 120 B. 128 C. 136 D. 144

题目
在下图中，大圆的半径是8。求阴影部分的面积是多少?



A. 120
B. 128
C. 136
D. 144
相似考题

1.如果大圆和小圆半径的比是2：1，则面积的比是4 : 2。（ ）

2.右图中的三角形纸板、正方形纸板、圆形纸板的面积都是40cm2，阴影部分的面积总和是30cm2，三张纸板盖住的总面积是70cm2。求三张纸板重叠部分的面积（即A的面积）为多少平方厘米？（）A. 10 B. 15 C. 6 D. 20

3.下图中，每个小正方形网格都是边长为1的小正方形，则阴影部分面积最大是： AA BB CC DD

4.：右图中的甲和乙都是正方形，BE=6厘米，EF=4厘米。那么，阴影部分ABC的面积是多少平方厘米？（ ）A．20B．24C．21D．18

更多“ 在下图中，大圆的半径是8。求阴影部分的面积是多少? ”相关问题

  • 第1题：

    三个圆的半径都是5cm,三个圆两两相交于圆心。求阴影部分的面积之和。


    A. 29.25cm
    B. 33.25cm
    C. 35.35cm
    D. 39.25cm

    答案：D
    解析：
    如图采用割补法,正好补成一个半圆.所以阴影部分的面积为 3.14×252 =39.25。故答案为D。

  • 第2题：

    设曲线y=4-x2(x≥0)与x轴，y轴及直线x=4所围成的平面图形为D(如
    图1—3—2中阴影部分所示)．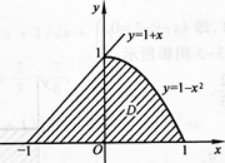

    图1—3—1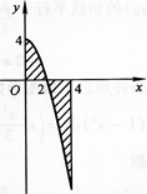

    图1—3—2
    ①求D的面积S；
    ②求图中x轴上方的阴影部分绕y轴旋转一周所得旋转体的体积Vy．


    答案：
    解析：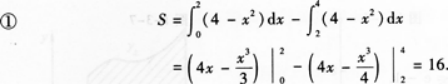

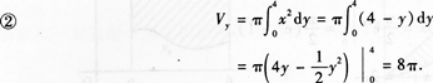
  • 第3题：

    下图中的甲和乙都是正方形，BE=6厘米，EF=4厘米。那么，阴影部分ABC的面积是多少平方厘米？（ ）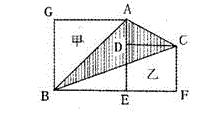


    A. 20
    B. 24
    C. 21
    D. 18

    答案：D
    解析：
    阴影部分ABC的面积等于整个图形面积减去△AGB和△BFC的面积，所以有6×6+4×4+1/2×2×4-1/2×6×6-1/2×10×4 =18平方厘米。故答案为D。

  • 第4题：

    如下图所示，已知线段DE与AC平行，且与圆的半径相等，都为3厘米，0为圆的圆心。求图中阴影部分的面积。(π取3．14)


    答案：
    解析：

  • 第5题：

    三个圆的半径都是5cm，三个圆两两相交于圆心。求阴影部分的面积之和。( )。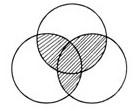

    A．29．25cm2 B．33．25cm2 C．39．25cm2 D．35．35cm2


    答案：C
    解析：
    使用割补法可知阴影部分的面积相当于半个圆的面积。故正确答案为C。

  • 第6题：

    本题图中，左边的图形每个小圆的面积为π，那么右边图形中阴影部分面积为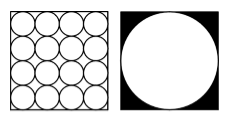

    A.8π
    B.64-16π
    C.4π+8
    D.20

    答案：B
    解析：
    第一步，本题考查的为平面几何问题。第二步，根据小圆的面积为π，则π·r2＝π，则r＝1，小圆的周长为正方形的边长等于4个小圆的直径，所以正方形的边长为··8。第三步，则阴影部分的面积为：正方形的面积－大圆的面积，其中大圆的半径为正方形边长的一半即8÷2＝4，则阴影部分的面积＝8×8－π×4×4＝64－16π。因此，选择B选项。

  • 第7题：

    如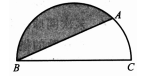，BC是半圆的直径，且BC=4，∠ABC=30°，则图中阴影部分的面积为



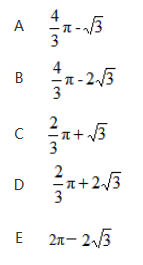    答案：A
    解析：

  • 第8题：

    如图所示，BC：6，AC=8，两个等圆外切，则图中阴影部分的面积为：

    A.25π/4
    B.25π/8
    C.25π/16
    D.25π/32

    答案：A
    解析：
    根据勾股定理可知AB=10，则两等圆的半径均为5，阴影部分的面积相当于圆心角为∠A﹢∠B的扇形的面积，即四分之一圆的面积，则所求为

  • 第9题：

    如左下图所示，大圆半径为小圆的直径，巳知图中，阴影部分面积为S1，空白部分面积为S2，那么这两个部分的面积之比约为（ ）。

    A. 1 : 1 B. 1：3 C. 3 : 5 D. 2 : 3


    答案：C
    解析：
    如图添加辅助线，小圆内部的阴影部分可以填到外侧来，这样，空白部分就是一个圆的内接正方形。
    设大圆半径为r，则S2=2r2 ，S1=πr2 -2r2所以S1: S2 = (3. 14-2) : 2 = 57 : 100。
    因此，本题正确答案为C。
    本题的解题关键是移动图形，找出图形之间的关系。

  • 第10题：

    如右图，一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动，当小圆盘围绕大圆盘中心转过90°后，小圆盘运动过程中扫过的面积是多少平方厘米？(π取3)( )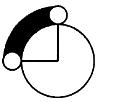

    A. 18 B. 15
    C. 12 D. 10


    答案：C
    解析：
    小圆盘运动过程中扫过的面积由两部分相减而成。
    第一部分：半径为6厘米，中心角为90°的扇形减去半径为4厘米，中心角为90°的扇形，面积为(62Xπ-42Xπ)/4 = 5π=15(平方厘米)。
    第二部分：半径为1厘米的2个小半圆，总面积是3平方厘米，所以扫过的面积为15-3 = 12(平方厘米)。
    因此，本题正确答案为C。

  • 第11题：

    由曲线y=x2，直线y=a，x=0及x=1所围成的图形如图3—4中阴影部分所示，其中0≤a≤1．

    (1)求图中阴影部分的面积A．
    (2)问a为何值时，A的取值最小，并求出此最小值．


    答案：
    解析：

  • 第12题：

    （）是面状地物最基本的参数。

    • A、最大圆弧半径
    • B、面积
    • C、周长
    • D、面的规则性

    正确答案:B

  • 第13题：

    如图所示，BC=6，AC=8，两个等圆外切，A、B分别为两圆的圆心，则图中阴影部分的面积为：


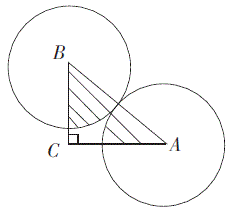    A.(25/4)π
    B.(25/8)π
    C.(25/16)π
    D.(25/32)π

    答案：A
    解析：
    根据勾股定理可知AB=10，则两个等圆的半径均为5，阴影部分的面积相当于圆心角为∠A+∠B的扇形的面积，即四分之一圆的面积，则所求为(1/4)π×5^2=(25/4)π。

  • 第14题：

    如图，Rt△ABC中，∠ABC=90o,AB=28 cm，以AB为直径的半圆与AC相交，图中的阴影部分①的面积比⑦的面积少28.28 cm2，求BC的长(π取3．14)。


    答案：
    解析：

  • 第15题：

    下图中阴影1的面积比阴影2的面积多28平方厘米，AB=40cm，BC垂直于AB，求BC 的长。（π 取 3.14）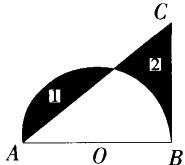


    A.20cm
    B.25cm
    C.30cm
    D.35cm

    答案：C
    解析：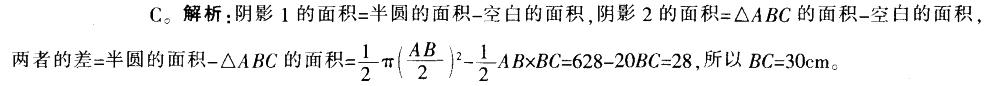

  • 第16题：

    在图中，大圆的半径是8，求阴影部分的面积是多少?（）[银行真题]

    A.120
    B.128
    C.136
    D.144


    答案：B
    解析：
    阴影部分形状不规则，对其进行割补，使之成为规则的几何图形，然后计算面积。
    在图中．由图形的对称性可知。正方形ABCD外部的8块阴影部分与正方形ABCD内部的8块空白面积相等。
    即通过割补．阴影部分面积等于正方形ABCD的面积．由题意大圆直径即为正方形的对角线。故正方形的面积是16×16÷2=128。

  • 第17题：

    如图，AD=DB=DC=10厘米，那么，图中阴影部分的面积是多少平方厘米？（）



    A. 109
    B. 110
    C. 107
    D. 110.25

    答案：C
    解析：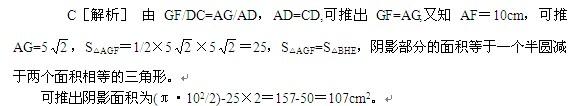

  • 第18题：

    如图，已知大圆的半径是5厘米，大圆里面有四个大小不等的小圆，这四个小圆的周长之和是多少厘米？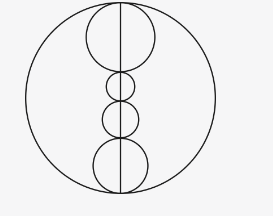

    A.10π
    B.15π
    C.20π
    D.5π

    答案：A
    解析：
    第一步，本题考查几何问题，属于平面几何类。
    第二步，设四个小圆直径为a、b、c、d，可知a＋b＋c＋d＝2×5＝10（厘米）。四个小圆周长之和应为π×（a＋b＋c＋d）＝π×10＝10π（厘米）。

  • 第19题：

    如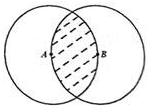，圆A与圆B的半径均为1，则阴影部分的面积为



    答案：E
    解析：

  • 第20题：

    图中的大正方形ABCD的面积是1平方厘米，其他点都是它所在边的中点。弧是一个内切于小正方形IJKL的半圆弧，PQ、OP是与弧半径相等的圆的四分之一圆弧，则阴影区的面积是多少平方厘米？（ ）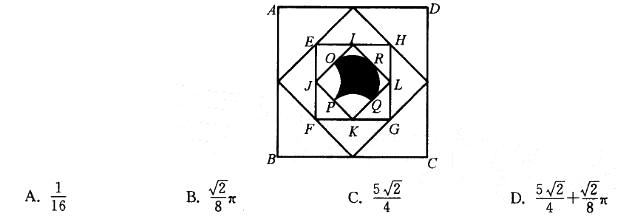


    答案：A
    解析：
    由正方形是大正方形面积的1/4，小正方形IJKL是正方形EFHG面积的1/2，故小正方形IJKL是大正方形ABCD面积的1/8，如下图所示，图中的阴影部分面积是小正方形IJKL 的一半，所以阴影区的面积为大正方形面积的1/16。A为正确选项。

  • 第21题：

    如右上图，正三角形的三个顶点都位于大圆周上，且三条边都与小圆相切。如果正三角形的边长是10厘米，那么图中圆环（阴影部分）的面积是多少平方厘米？ (π=3. 14)( )

    A. 12.56 B. 78.5 C. 314 D. 512.6


    答案：B
    解析：
    连接圆心O与三角形的顶点A及三角形与小圆相切的切点B（见右图）。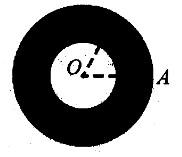

    S圆环 = (OA2-OB2)π= BA2π
    =(10/2)2 π
    =78.5(平方厘米)
    因此，本题正确答案为B。

  • 第22题：

    已知图中三角形ABC的面积为1998平方厘米，是平行四边形DEFC面积的3倍。那么，图中阴影部分的面积是多少平方厘米？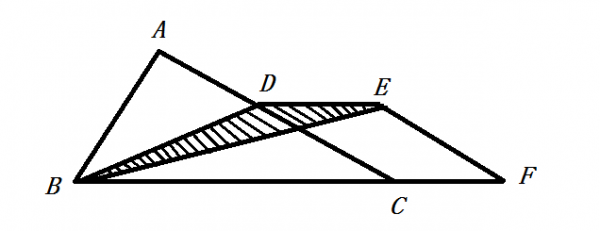


    A. 333
    B. 499
    C. 999
    D. 1333

    答案：A
    解析：
    由图得阴影部分与平行四边形同底等高,所以阴影部分面积是平行四边形的一半，
    因为三角形ABC的面积是1998平方厘米，是平行四边形DEFC的3倍，所以三角形ABC的面积是阴影部分的6倍，则阴影部分面积是8325px2。故选A选项。

  • 第23题：

    计算题：一砂轮片，半径为25厘米，该砂轮片中心轴孔半径为8厘米，求砂轮片的有效面积？


    正确答案: S=（25-8）²π=907.5（厘米）²

相关内容