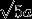A和B为正方体两个相对的顶点，一个点从A出发沿正方体表面以最短路径移动到B，则其可选择的路线有几条？( ) A. 2 B. 3 C. 6 D. 12

题目
A和B为正方体两个相对的顶点，一个点从A出发沿正方体表面以最短路径移动到B，则其可选择的路线有几条？( )

A. 2
B. 3
C. 6
D. 12
相似考题

1.将正方体的表面沿某些棱剪开，展成一个平面图形，你剪开了几条棱？与同伴进行交流，你们的结果是否一致？

2.关键路径是指AOE(Activity On Edge)网中(38)。A．最长的回路B．最短的回路C．从源点到汇点(结束顶点)的最长路径D．从源点到汇点(结束顶点)的最短路径

3.关键路径是指AOE(Activity On Edge)网中______。A．最长的回路B．最短的回路C．从源点到汇点(结束顶点)的最长路径D．从源点到汇点(结束顶点)的最短路径

4.一个正八面体两个相对的顶点分别为A和B，一个点从A出发，沿八面体的棱移动到B位置，其中任何顶点最多到达1次，且全程必须走过所有8个面的至少1条边，问有多少种不同的走法？（ ）A．8 B．16 C．24 D．32

参考答案和解析
答案：C
解析：
几何问题。从一个顶点到最远顶点的最短路径，从一个顶点连接的有三个平面,一个平面有两种路径，所以有6条不同路径。
更多“A和B为正方体两个相对的顶点，一个点从A出发沿正方体表面以最短路径移动到B，则其可选择的路线有几条？( ) ”相关问题

  • 第1题：

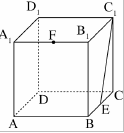
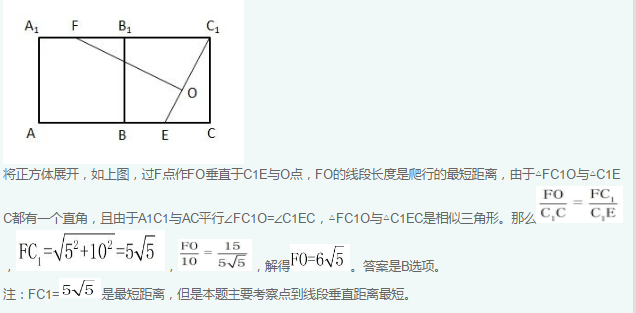
    如右图所示，一个边长为10厘米的正方体木块ABCD-A1B1C1D1，点E、F分别是BC、A1B1的中点，C1E是用蜂蜜画的一条线段，一只蚂蚁在点F处，要想沿正方体表面最快到达蜂蜜所在线段C1E，它所爬行的最短距离是多少厘米？




    答案：B
    解析：
    知识点:体积计算

  • 第2题：

    一只蚂蚁从右图的正方体的A顶点沿正方体的表面爬到正方体的C顶点，设正方体边长为a，问该蚂蚁爬过的最短路程为：



    答案：B
    解析：

  • 第3题：

    一个正方体的边长为1，一只蚂蚁从其一个角出发，沿着正方体的棱形进，直到经过该正方体的每一条棱为止（经过一个顶点即算作经过该顶点所连接的3条棱）。则其最短的行进距离为（ ）。

    A. 3
    B. 4
    C. 5
    D. 6

    答案：C
    解析：
    蚂蚁行进路径如下图2所示，故本题答案为C选项。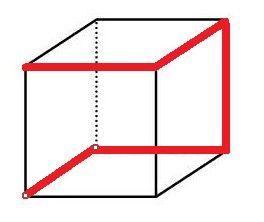

  • 第4题：

    一只蚂蚁位于2×2×2正方体空心框架的A点，向B点爬行。如果只准沿着框架线条爬，则最短路线一共有几条?

    {图}

    A.64
    B.90
    C.99
    D.100

    答案：C
    解析：
    要求最短路径，则蚂蚁在每个点只能向上、前、右爬。记向右爬为x，向前爬为)，，向上爬为z，则路径相当于对xxyyzz进行排列，有c：xC：=90，选8。

  • 第5题：

    一只蚂蚁从右图的正方体的A顶点沿正方体的表面爬到正方体的C顶点，设正方体边长为a，问该蚂蚁爬过的最短路程为：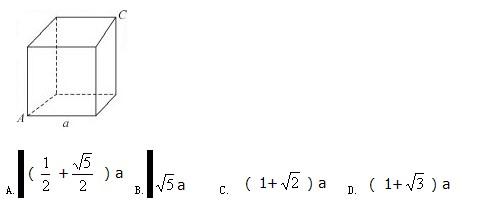

    A.

    A B. B C. C D. D

    答案：B
    解析：
    解题指导： 该最短路程为√[1+﹙22a﹚]=√5a。故答案为B。

  • 第6题：

    把若干个体积相等的正方体拼成一个大正方体,在表面涂上红色,已知一面涂色的小正方体有96个,则两面涂色的小正方体有（ ）个

    A.48
    B.60
    C.64
    D.24
    E.32

    答案：A
    解析：
    一面涂色的小正方体位于大正方体的面上（除去機上的）,每个面有4×4=16（个）,令小正方体的边长为1,则大正方体的边长为6;两面涂色的小正方体位于大正方体的機上（除去8个角）,每条棱上有4个,故总个数为4×12=48

  • 第7题：

    以正方体的8个顶点为节点，连成一条含8个线段的不自交闭折线，两个节点间必须以直线连接。问这个闭折线至少有几段与正方体的棱重合？

    A.0
    B.1
    C.2
    D.4

    答案：B
    解析：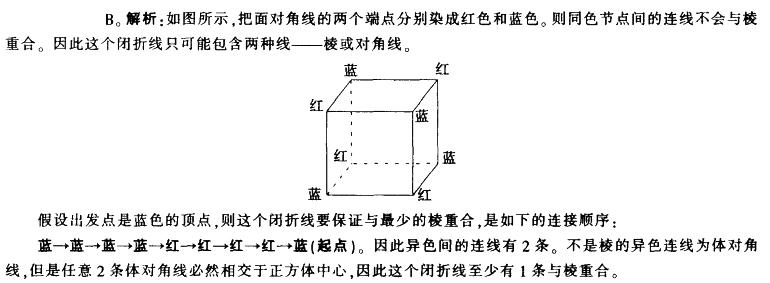

  • 第8题：

    A和B为正方体两个相对的顶点，一个点从A出发沿正方体表面以最短路径移动到B，则其可选择的路线有几条（）

    • A、2
    • B、3
    • C、6
    • D、12

    正确答案:C

  • 第9题：

    在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：

    A.1/4
    B.1/6
    C.1/8
    D.1/10

    答案：C
    解析：
    由题意知切下的角是底面为正三角形、侧面为三个等腰直角三角形的三棱锥，设切下角的直角边为ｘ，则六面体体积＝2×三棱锥体积＝2×(1/3)×(ｘ2/2)×ｘ＝1/24，解得ｘ＝1/2。所以六面体每个面是直角边为1/2的等腰直角三角形，六面体的每个面相当于边长为1的正方形面积的1，所以六面体的表面积为原正方体的1/8。故本题选C。

  • 第10题：

    一个木制正方体在表面涂上颜色，将它的每条棱三等分，然后从等分点将正方体展开，得到27个小正方体，将这些小正方体充分混合后，装入一个口袋，从这个口袋中随机取出两个小正方体，其中一个正方体只有一个面涂有颜色，另一个只有2个面涂有颜色的概率约为（ ）

    A. 0.05
    B. 0.17
    C. 0.34
    D. 0.67

    答案：C
    解析：
    涂一面的6个 涂2面的12个 满足条件情况72个，经计算为0.34

  • 第11题：

    数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
    一只蚂蚁从图的正方体A顶点沿正方体的表面爬到正方体C顶点。设正方体边长为a，问该蚂蚁爬过的最短路程为（）。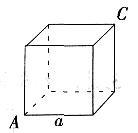

    A.
    B.
    C.
    D.


    答案：B
    解析：
    根据两点之间线段最短，将正方体展开为平面。根据勾股定理A到C的直线距离为。

  • 第12题：

    有l25个棱长均为1的正方体，其中100个表面为白色，25个表面为蓝色。将这些正方体组成一个大正方体，表面为白色的面积至少为( )。’

    A.100
    B.97
    C.94
    D.92

    答案：D
    解析：
    题目可转化为表面为蓝色的面积至多为多少，则应把蓝色小正方体尽量放在角和棱上，这样每个小正方体可贡献3个或2个蓝色表面。因此在8个角上用去8个蓝色正方体后，在棱上再放25—8=17个，此时蓝色表面积最大为3×8+17x2=58，表面为白色的面积至少为25×6—58=92．选D。

  • 第13题：

    一个正八面体两个相对的顶点分别为A和B，一个点从A出发，沿八面体的棱移动到B位置，其中任何顶点最多到达1次，且全程必须走过所有8个面的至少1条边，问有多少种不同的走法？（ ）
    A．8 B．16 C．24 D．32


    答案：A
    解析：
    本题属于几何问题。在如图所示的正八面体中，假设从最上面的A点出发，要达到最下面的B点，首先要经过中间平面上的四个点，此时4条路线是对称的。假设从A先到点1，下一步有点2和点4两种选择，此时已经有4×2=8种路线。但从点2走到点3之后，不能直接到B点，必须再经过点4，否则不满足“走过所有8个面的至少1条边”，因此总的走法就是8种。所以选择A选项。

  • 第14题：

    一只蚂蚁位于2×2×2正方体空心框架的A点，向B点爬行。如果只准沿着框架线条爬。则最短路线一共有几条?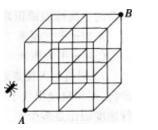

    A.64
    B.90
    C.99
    D.100

    答案：B
    解析：
    要求最短路径，则蚂蚁在每个点只能向上、前、右爬。记向右爬为x，向前爬为y，向上爬为

  • 第15题：

    如图，A，B是棱长为1的正方体的两个顶点，将正方体按图中所示展开，则在展开图中A，B两点间的距离为( )。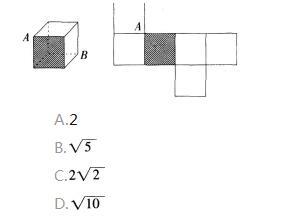


    答案：B
    解析：

相关内容