如图,ABCD为矩形,AB=4,BC=3,边CD在直线L上,将矩形ABCD沿直线L作无滑动翻转,当点A第一次翻转到点A1位置时,点A经过的路线长为:A7π B6π C3π D3π/2
题目
如图,ABCD为矩形,AB=4,BC=3,边CD在直线L上,将矩形ABCD沿直线L作无滑动翻转,当点A第一次翻转到点A1位置时,点A经过的路线长为:
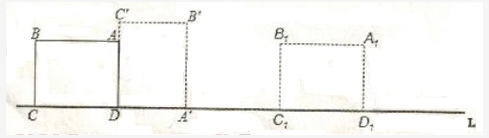
A7π
B6π
C3π
D3π/2

A7π
B6π
C3π
D3π/2
相似考题
更多“如图,ABCD为矩形,AB=4,BC=3,边CD在直线L上,将矩形ABCD沿直线L作无滑动翻转,当点A第一次翻转到点A1位置时,点A经过的路线长为: ”相关问题
-
第1题:
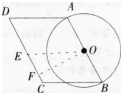
如图,四边形ABCD中,AB=10,AD=m,∠D=60o,以AB为直径作⊙O。
(1)求圆心0到CD的距离(用含m的代数式表示);
(2)当m取何值时,CD与⊙0相切?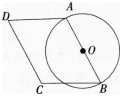 答案:解析:
答案:解析:
-
第2题:
如图。在直角梯形ABCD中,AB∥CD,∠BAD=90o,且AB=8,AD=3,CD=4,动点P,Q分别以点B和点A为起点同时出发,点P沿B→A,以每秒1个单位速度运动,终点为点A;点Q沿A→D→C→B,以每秒1.5个单位速度运动,终点为点B。设△APQ的面积为y,运动时间为x。
(1)求y关于x的函数解析式y=f(x);
(2)画出函数y=f(x)的图象。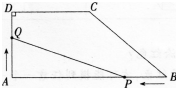 答案:解析:
答案:解析:
(2)函数图象如图所示: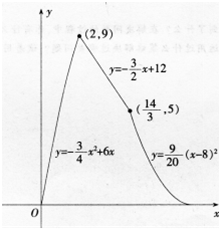
-
第3题:
如下图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.
 答案:解析:证明:如右图所示,∵四边形ABCD为平行四边形,∴BO=DO,
答案:解析:证明:如右图所示,∵四边形ABCD为平行四边形,∴BO=DO,
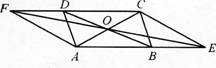
又∵AB∥CD,∴∠FDO=∠EB0

-
第4题:
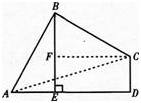
如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.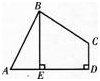
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.答案:解析: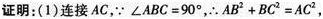
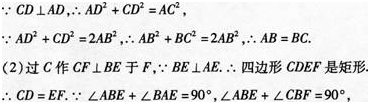

-
第5题:
如图,平面四边形ABCD中,AB=2,BC=4,CD=5,DA=3,
(1)若∠B与∠D互补,求AC2的值;
(2)求平面四边形ABCD面积的最大值。 答案:解析:
答案:解析: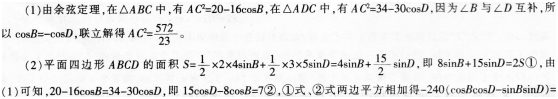
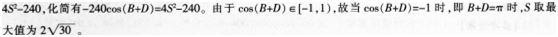
-
第6题:
如图所示,梯形ABCD的两条对角线AD、BC相交于O,EF平行于两条边且过O点。现已知AB=6,CD=18。问EF的长度为多少?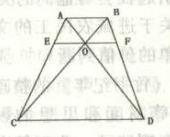 A. 8.5
A. 8.5
B. 9
C. 9.5
D. 10答案:B解析:解题指导: 18*BF/BD=6*DF/BD, BF/DF=1:3, OF/CD=1:4, OE/CD=1:4, EF=CD/2=9,故答案为B。 -
第7题:
在电线悬挂点等高时,两悬点间的直线距离为档距l(m),沿电线曲线的长度为线长L(m)。
LGJ-400/50,悬点等高,l=400m,覆冰弧垂为13.4m,其电线长度为()。
A.401.2m; B.402.1m; C.403.2m; D.404.3ra。答案:A解析:根据《电力工程髙压送电线路设计手册》(第二版)。179页表3-3-1,
L=l+8f2/3l
-
第8题:
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。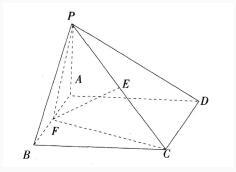 答案:解析:
答案:解析:
-
第9题:
如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P是BC边的中点,AD=2,SA=AB=1。

(1)求证:PD⊥平面SAP;
(2)求三棱锥S-APD的体积。答案:解析:(1)证明:易知在△APD中,,AD=2,满足勾股定理,故PD⊥AP。SA⊥底面ABCD,则SA⊥PD。PD同时垂直于平面SAP内的两条相交直线,PD⊥平面SAP。 (2)
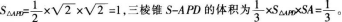
-
第10题:
在矩形ABCD中,AB=16cm,AD=6cm,动点P、Q分别从A、C两处出发,点P以3cm/s的速度向点B移动,一直到点曰,点Q以2cm/s向D移动,当P,Q距离为10cm时,P、Q两点从出发开始经过时间为( )s。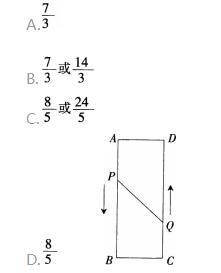 答案:C解析:
答案:C解析:
-
第11题:
汽车由静止开始从A点沿直线ABC作匀变速直线运动,第4s末通过B点时关闭发动机,再经6s到达C点时停止。已知AC的长度为30m,则下列说法正确的是()
- A、通过B点时速度的3m/s
- B、通过B点时速度是6m/s
- C、AB的长度为12m
- D、汽车在AB段和BC段的平均速度相同
正确答案:B,C,D -
第12题:
填空题已知点O到直线l上一点P的距离为3cm,圆O的半径为3cm,则直线l与圆的位置关系是____.正确答案: 相切或相交解析: 暂无解析 -
第13题:
(6分)如图,点P为矩形ABCD边BC上一点(不包括端点),E为BC延长线上一点,CQ为∠DCE的角平分线,连接AP,PQ,使AP⊥PQ。求证:当AB=BC时,存在AP=PQ。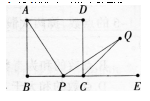 答案:解析:
答案:解析:
∴AP=PQ。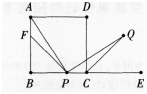
-
第14题:
如图,四边形ABCD与四边形DEFG都是矩形,顶点F在BA的延长线上,边DG与AF交于点H,AD=4,DH=5,EF=6,求FG的长.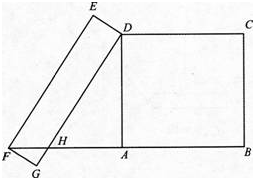 答案:解析:解:∵四边形ABCD和四边形DEFG均为矩形,
答案:解析:解:∵四边形ABCD和四边形DEFG均为矩形,
∴∠DAF=∠DAB=90°,∠G=90°,DG=EF.
∵EF=6,DH=5,∴GH=DG-DH=EF-DH=6-5=1
在Rt△ADH中,AD=4,DH=5,

-
第15题:
如图,P是矩形ABCD内一点,若PA=3,PB=4,PC=5,则PD=_______。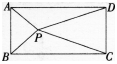 答案:解析:
答案:解析: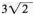
解析:矩形内的点到相对顶点的距离平方和相等,即PA2+PC2=PB2+PD2,即32+52=42+PD2,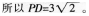
-
第16题:
如图,边长为a的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=________。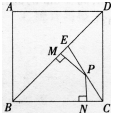 答案:解析:
答案:解析: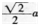
解析:作EK⊥BC于K,连接BP,由△EBC的面积等于△PBE和△PBC的面积之和且BE=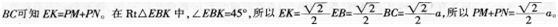
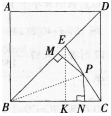
-
第17题:
如图,在矩形ABCD中,AB=5,BC=12,将矩形ABCD沿对角线对折放在桌面上,折叠后所成的图形覆盖桌面的面积是 答案:解析:
答案:解析: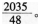
解析:

-
第18题:
长方形ABCD,从图示的位置开始沿着AP每秒转动90度(无滑动情况),AB=4厘米,BC=3厘米,当长方形的右端到达距离A为46厘米的位置时是( )秒后。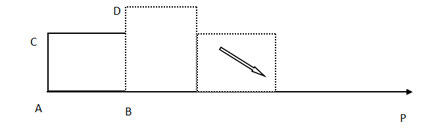 A. 11
A. 11
B. 12
C. 13
D. 14答案:B解析:长方形边长为AB=4,BC=3,向右转动时,底边的边长依次是3,4,3,4,3,4……,每移动两次可以移动7厘米,故6个轮次之后可以移动42厘米,也就是12次之后,加上之前的4厘米刚好到46厘米处。 -
第19题:
在电线悬挂点等高时,两悬点间的直线距离为档距l(m),沿电线曲线的长度为线长L(m)。
LGJ-400/50,其悬点等高,l=400,最髙气温时弧垂为16m,其线长为()。
A.400.8m; B.401.7m; C.402.5m; D.404.3m.答案:B解析:根据《电力工程髙压送电线路设计手册》(第二版)。179页表3-3-1,
L=l+8f2/3l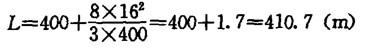
-
第20题:
如图,在一张矩形纸片ABCD中,AB=4,BC=8。点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点日处,点D落在G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时, 。以上结论中,你认为正确的有( )个。 A.1
A.1
B.2
C.3
D.4答案:C解析:
-
第21题:
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。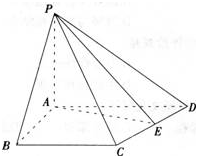 答案:解析:
答案:解析:
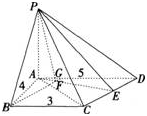
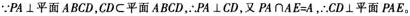

-
第22题:
以直线AB为例,从直线上开始,绘制AB的垂线CD,其中D点在直线AB上.C点在直线外,下面描述中,那些是正确的()
- A、拖动B点,D点随之不动,C点随之而动
- B、拖动D点,D点在直线AB上变化位置,C点位置随之而变
- C、拖动C点,C点在直线AB外变化位置,D点在直线AB上变化位置
- D、拖动直线AB点随之而动C点随之而动
正确答案:A,B,D -
第23题:
在铰链四杆机构ABCD中,已知AB=25mm,BC=70mm,CD=65mm,AD=95mm,当AD为机架时,是()机构;当AB为机架时,是()机构。
正确答案:曲柄摇杆机构;双曲柄机构
