如图,在长方形跑道上,甲、乙两人分别从A、C处同时出发,按顺时针方向沿跑道匀速奔跑。已知甲、乙两人的速度分别为5米/秒、4.5米/秒。则当甲第一次追上乙时,甲沿长方形跑道跑过的圈数是:A.4 B.4.5 C.5 D.5.5
题目
如图,在长方形跑道上,甲、乙两人分别从A、C处同时出发,按顺时针方向沿跑道匀速奔跑。已知甲、乙两人的速度分别为5米/秒、4.5米/秒。则当甲第一次追上乙时,甲沿长方形跑道跑过的圈数是:
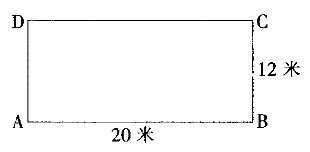

A.4
B.4.5
C.5
D.5.5
B.4.5
C.5
D.5.5
相似考题
更多“如图,在长方形跑道上,甲、乙两人分别从A、C处同时出发,按顺时针方向沿跑道匀速奔跑。已知甲、乙两人的速度分别为5米/秒、4.5米/秒。则当甲第一次追上乙时,甲沿长方形跑道跑过的圈数是: ”相关问题
-
第1题:
环形跑道周长是500 米,甲、乙两人按顺时针沿环形跑道同时、同地起跑,甲每分钟跑60 米,乙每分钟跑50 米,甲、乙两人每跑200 米均要停下来休息1 分钟,那么甲首次追上乙需要多少分钟?
A.60 B.36 C.77 D.103
正确答案:C
-
第2题:
甲、乙分别从A、C同时出发顺时针方向匀速跑步,甲的速度为5m/s,甲第一次追上乙时已经跑了5圈刚好回到A。求乙的速度为多少m/s? A.4.8
A.4.8
B.4.5
C.4
D.3答案:B解析:甲第一次追上乙时跑了5圈,因为出发时相距0.5圈,因此乙跑了4.5圈,则甲、乙的速度之比为5:4.5,甲的速度为5m/s,则乙为4.5m/s。 -
第3题:
在400米环形跑道上,A、B两点最近相距100米(如图)。甲、乙两位运动员分别从A、B两点同时出发,按逆时针方向跑步,甲每秒跑9米,乙每秒7米,他们每人跑100米都停5秒,那么追上乙需要多少秒?( )

A. 70
B. 65
C. 75
D. 80答案:D解析:解题指导: 甲每跑100/9休息5秒,100/9+5=16(1/9);乙每跑100/7秒休息5秒,100/7+5=19(2/7)。比较分析,结合选项,考虑出发后75秒时的情况,甲休息了四次,跑了(75—4×5)×9=495米;乙跑了400米。甲比乙多跑了95米,甲没有追上乙。所以甲追上乙的时间应大于75秒。故答案为D。 -
第4题:
如图,学校操场的400米跑道中套着300米小跑道.大跑道与小跑道有200米路程相重。甲以每秒6米的速度沿大跑道逆时针方向跑,乙以每秒4米的速度沿小跑道顺时针方向
跑.NANN 从两跑道的交点A处出发,当他们第二次在跑道上相遇时,甲共跑了多少米?
 A.480
A.480
B.540
C.660
D.720答案:B解析:根据题意可知,甲、乙只可能在AB右侧的半跑道上相遇。易知小跑道上AB左侧的路程为100米,右侧的路程为200米,大跑道上AB的左、右两侧的路程均是200米。当甲第一次到达B点时,乙还没有到达8点,所以第一次相遇一定在B点右侧某处。而当乙跑完一圈到达A点需要300.'-4=75秒.甲跑了6×75=450米,在A点左边50米处。所以当甲再次到达B处时,乙还未到B处.那么甲必定能在B点右边某处与乙第二次相遇。从乙再次到达A处开始计算,还需(400—50)÷(6+4)=35秒,甲、乙第二次相遇,此时甲共跑了75+35=110秒,从开始到甲、乙第二次相遇甲共跑了6x110=660米,应选择C。 -
第5题:
甲、乙两人在400米环形跑道上从同一起点反向匀速慢跑,甲的速度为5米/秒,乙的速度为3米/秒,则甲、乙两人经过 再次在起跑点相遇。A.4分10秒
B.5分50秒
C.6分40秒
D.7分30秒答案:C解析:第一步,本题考查行程问题,属于相遇追及类。
第二步,要使甲乙再次在起跑点相遇,则甲跑过的距离一定为400的整数倍,设甲跑了n圈,所用时间为t,可得5t=400n,故时间t一定为80的倍数,四个选项的时间分别为250秒、350秒、400秒和450秒,只有C选项符合。
因此,选择C选项。 -
第6题:
有一个400米环形跑道,甲、乙两人同时从同一地点同方向出发,甲以0.8米/秒的速度步行,乙以2.4米/秒的速度跑步,乙在第2次追上甲时用了( )秒A.200
B.210
C.230
D.250
E.500答案:E解析:乙第2次追上甲时,乙比甲多跑了2圈,即多跑了800米,故所用时间为800/(2.4-0.8)=500(秒) -
第7题:
单选题一条圆形跑道长500米,甲、乙两人从不同起点同时出发,均沿顺时针方向匀速跑步。已知甲跑了600米后第一次追上乙,此后甲加速20%继续前进,又跑了1200米后第二次追上乙。问甲出发后多少米第一次到达乙的出发点?( )A180
B150
C120
D100
正确答案: A解析:
赋值甲的速度为100米/分,第一次追及,甲跑了600米,用时为6分;第二次追及,甲加速20%,即速度为120米/分,又跑了1200米,用时为10分。行程问题追及公式为:S差=v差t,从第一次追及开始,到第二次追及时,两人的路程差为1圈,即500=(120-v乙)×10,解得v乙=70米/分。分析第一次追及过程可知,甲比乙多走的距离即为甲出发点到乙出发点距离,S差=v差t=(100-70)×6=180米。故正确答案为A。 -
第8题:
单选题一个长方形的跑道,宽50米,长100米,甲乙两人在跑道上跑步,若两人同时同地背向出发,经30秒后相遇,若两人同时同地同向出发,经过75秒钟后,甲追上乙。现在两人在同一地点顺时针跑步,乙提前1分钟出发,问再经过多少秒甲才能追上乙?()A35
B40
C45
D50
正确答案: A解析: 暂无解析 -
第9题:
甲、乙、丙三人沿圆形跑道跑步,同时从跑道某一固定点出发,甲按顺时针方向行走,乙与丙按逆时针方向行走,甲第一次遇到乙2分钟后遇到丙,再过8分钟第二次遇到乙。已知乙的速度是甲的2/3,圆形跑道的周长为600米,则丙的速度为( )。A. 14米/分
B. 15米/分
C. 16米/分
D. 17米/分答案:A解析:行程问题。在环形相遇问题中,任意两者相遇一次所走的路程和为一个周长,因此,甲与乙第二次相遇共走的路程(1200米)是第一次相遇共走的路程(600米)的2倍,由于二者速度不变,设第一次的相遇所用时间为t,则第二次相遇时间应为2t,根据题意有2t=t+2+8,解得t=10分钟。再设甲、乙、丙的速度分别为、、,则(+)×10=600,(+V丙)×(10+2)=600,又,解得=36米/分,=14米/分。故本题选择A。 -
第10题:
环形跑道的周长为400米,甲乙两人骑车同时从同一地点出发,匀速相向而行,16秒后甲乙相遇。相遇后,乙立即调头,6分40秒后甲第一次追上乙,问甲追上乙的地点距原来的起点多少米?A. 8
B. 20
C. 180
D. 192答案:D解析:
-
第11题:
甲乙二人沿环形跑道从同一地点同时背向开始跑步,35秒后两人相遇。已知甲跑一圈需要60秒,乙跑一圈需要多少秒?A.77
B.84
C.91
D.96答案:B解析:第一步,本题考查行程问题的环形相遇问题,用相遇公式和基本行程公式解题。
-
第12题:
一个正方形跑道边长为20米,甲和乙从跑道上的不同位置同时出发,匀速沿逆时针跑步,已知两人出发的位置之间直线距离为20米,甲以2米/秒的速度跑6秒到达某个顶点后,又跑了不到10秒正好到达乙出发的位置,此时乙正好第二次跑到顶点位置。问以下哪个描述是正确的?( )A.甲出发后不到2分钟第一次追上乙
B.甲出发后超过2分钟第一次追上乙
C.乙出发后不到2分钟第一次追上甲
D.乙出发后超过2分钟第一次追上甲答案:A解析:本题属于行程问题。
由甲以2米/秒的速度跑6秒到达某个顶点,画出图示。如图所示: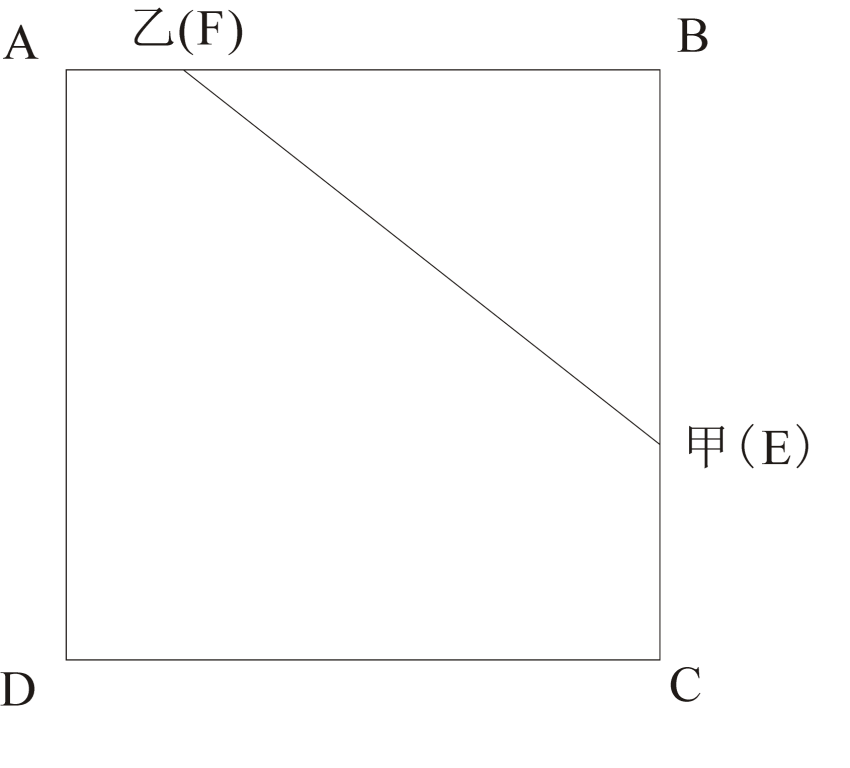
甲初始位置在E点,EB=6×2=12米,由题意又跑了不到10秒正好到达乙出发的位置,所以画出示意图乙出发点在F点,且EF=20。由勾股定理可求得BF=16。甲到达乙的出发点共用时(12+16)÷2=14秒。又因为此时乙正好第二次跑到顶点位置,即跑到了D点,所以乙的速度为(4+20)÷14=12/7。甲的速度大于乙的速度,所以甲出发后,追上乙需要的时间为(12+16)÷(2-12/7)=98s。A符合题意。
因此,选择A选项。 -
第13题:
在400米环形跑道上,A、B两点相距100米,甲、乙两人分别从A、B两点同对出发,按逆时针方向跑步,甲每秒跑5米,乙每秒跑4米,他们每人跑100米,都要停10秒钟。求甲追上乙需多少秒?()
A. 100 B. 130 C. 140 D. 150答案:C解析:如果甲、乙两人不停地跑,可以计算出甲追上乙的时间,再加上中间停留的时间就是所求时间。如果甲、乙跑步不停留,甲追上乙需要100/(5- 4) = 100(秒);甲跑100秒,共跑5X100 = 500(米);他在跑出100米、200米、300米、400米处共停留了4次,到了500米处恰好追上乙,不必计停留时间。所以甲追上乙需要的时间是100 + 4X10=140(秒)。因此,本题正确答案为C。 -
第14题:
在400米环形跑道上,A、B两点相距100米,甲、乙两人分别从A、B两点同时出发,按逆时针方向跑步,甲每秒跑5米,乙每秒跑4米,他们每人跑100米,都要停10秒钟。求甲追上乙需多少秒?( )
A. 100 B. 130 C. 140 D. 150答案:C解析:如果甲、乙两人不停地跑,可以计算出甲追上乙的时间,再加上中间停留的时间就是所求时间。如果甲、乙跑步不停留,甲追上乙需要100/(5-4) = 100(秒);甲跑100秒,共绝5X100 = 500(米);他在跑出100米、200米、300米、400米处共停留了4次,到了500米处恰好追上乙,不必计停留时间。所以甲追上乙需要的时间是100 + 4X10=140(秒)。因此,本题正确答案为C。 -
第15题:
单选题一个正六边形跑道,每边长为100米,甲乙两人分别从两个相对的顶点同时出发,沿跑道相向匀速前进,第一次相遇时甲比乙多跑了60米,则甲跑三圈时,两人之间的直线距离是多少?( )A100米
B150米
C200米
D300米
正确答案: B解析:
第一次相遇时甲比乙多跑60米,则相遇时乙跑了(300-60)÷2=120米,甲跑了180米,两者的速度比为180:120。设甲跑了三圈时,乙跑过的距离为x,180:120=(60×3):x,得x=1200,刚好为两圈。因此甲跑三圈时,两人都回到自己的出发点,即为相对的顶点,其直线距离为200米。
